8 VI zapraszamy wszystkich entuzjastów na XXII Mistrzostwa Polski w Geometrii Elementarnej do Instytutu Matematycznego UWr.
W Mistrzostwach wzięli udział koledzy: Dominik Bysiewicz, Radosław Górzyński i Robert Ciężabka. Dominik Bysiewicz zajął II miejsce. Gratulacje!
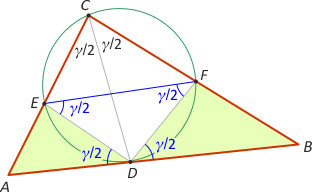
Zad. 1. W trójkącie ABC, okrąg przechodzący przez wierzchołek C i styczny do boku AB w punkcie D będącym spodkiem dwusiecznej kąta C, przecina boki AC i BC odpowiednio w punktach E i F. Wiedząc, że |AE|:|BF| = 2/3, oblicz stosunek pól trójkątów ADE i DBF.
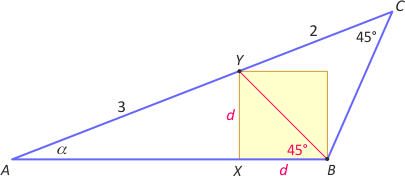
Zad. 2. W trójkącie ABC |∡B| > 90° a |∡C| = 45°. Na bokach AB i AC obrano odpowiednio punkty X i Y takie, że wraz z punktem B są wierzchołkami kwadratu. Wiedząc, że |AY|=3 i |YC|=2, oblicz pole tego kwadratu.
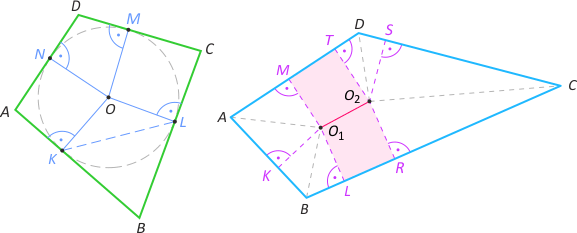
Zad. 3. Wykaż, że dowolny czworokąt wypukły można podzielić na 5 wielokątów posiadających oś symetrii.
Zad. 4. (wolna amerykanka) W trójkącie ABC, dwusieczna AL przecina wysokości BD i CE w punktach K i M odpowiednio. Wiedząc, że |BK|:|KD| = 2 i |ME|:|KD| = 3/2, oblicz stosunek pola trójkąta DBC do pola koła na nim opisanego.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 pkt. - Dominik Bysiewicz (student matematyki na UJ), Robert Ciężabka (korepetytor, Osiek Jasielski), Radosław Górzyński (uczeń I LO Lubin), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia),
- 22 pkt. - Elżbieta Grzechnik (emerytowana nauczycielka z Radomia) oraz Marzena Wąsiewicz (nauczycielka z Kajetan).
Za zadanie 4 punkty otrzymali:
- 10 pkt. - Robert Ciężabka, Elżbieta Grzechnik, Radosław Górzyński,Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek, Tadeusz Porzucek oraz Marzena Wąsiewicz,
- 8 pkt. - Dominik Bysiewicz.
Gratulacje!
Zad. 1. Z równości miar kątów wpisanych DEF i ECD oraz kąta dopisanego ADE wynika, że odcinki EF i AB są równoległe, a tym samym, że szukany stosunek pól trójkątów równy jest stosunkowi
|AD|:|DB|. Z twierdzenia Talesa mamy 2/3 = |AE|:|FB| = |AC|:|BC|. Z kolei z twierdzenia o dwusiecznej kąta wewnętrznego mamy |AD|:|DB| = |AC|:|BC| = 2/3. Ostatecznie PADE : PDBF = 2/3.
Zad. 2. Prowadzimy przekątną BY. Zauważmy, że trójkąty ABC i ABY są podobne w skali k =
|AC|:|AB| = |AB|:|AY|, skąd |AB|2 = |AY|·|AC| = 15, czyli |AB| = √15. Z twierdzenia Pitagorasa w trójkącie AXY otrzymujemy 9 = (√15–d)2 + d2, skąd Pkw = d2 = (9–3√5)/2.
Zad. 3. Rozważmy dwa przypadki.
1) |AB|+|CD| = |BC|+|AD|. Wówczas na czworokącie można opisać okrąg, którego środek dzieli czworokąt na cztery deltoidy. Jeden z deltoidów można podzielić na dwa trójkąty równoramienne.
2) |AB|+|CD| ≠ |BC|+|AD|. Wpisujemy okręgi styczne do boków AB, BC i AD oraz BC, CD i AD o środkach odpowiednio O1 i O2. Otrzymujemy cztery deltoidy oraz sześciokąt O1LRO2TM, którego osią symetrii jest prosta O1O2. Jeden z deltoidów dzielimy jak w przypadku 1).
Zad. 4. (wolna amerykanka) Z twierdzenia o dwusiecznej |AD|:|AB| = |DK|:|KB| = 1/2, co oznacza, że trójkąt ABD jest ekierkowy i |<ABD|=30°. Oznaczmy |BD|=3d. Wówczas |AD|=d√3 i |AB|=2d√3. Trójkąty AME i AKD są podobne w skali k = |ME|:|KD| = 3/2, skąd |ME|=3d/2. Dalej w trójkącie ABD mamy α=60°, skąd trójkąt AEM jest także ekierkowy i |AE|=3d√3/2. Z kolei w trójkącie ekierkowym AEC mamy |AC| = 2·|AE| = 3d√3. Rozważmy teraz trójkąt DBC, w którym
|DC| = |AC|–|AD| = 2d√3, skąd PDBC = |DC|·|DB|/2 = 3d2√3. Dalej Pkoł = π(|BC|/2)2 =
(π/4)·(|BD|2+|DC|2) = (21π/4)d2. Ostatecznie PDBC/Pkoł = (4√3)/7π.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
