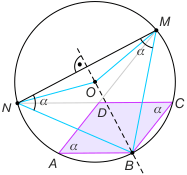
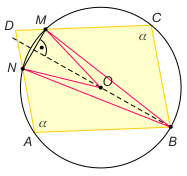
Zadanie 1. Okrąg o środku O przechodzi przez wierzchołki A,B, C równoległoboku ABCD i przecina prostą AD w punkcie M, a prostą CD w punkcie N. Wykaż, że BO jest prostopadły do MN.
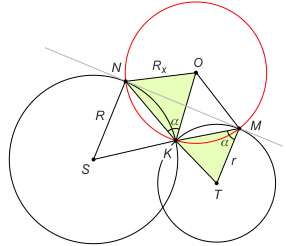
Zadanie 2. Okręgi o promieniach R i r przecinają się w punkcie K. Niech M i N są punktami styczności tych okręgów ze wspólną styczną. Oblicz promień okręgu opisanego na trójkącie KMN.
Zadanie 3. Oblicz kąty trójkąta, wiedząc, że środki okręgów wpisanego w ten trójkąt i opisanego na tym trójkącie są położone symetrycznie względem boku.
Zadanie 4. (wolna amerykanka) Dany jest trójkąt prostokątny ABC. Prosta równoległa do przeciwprostokątnej AB przecina bok AC w punkcie D, a bok BC - w punkcie E, przy czym |DE|=2 oraz |BE|=1. Na przeciwprostokątnej obrano punkt F taki, że |BF|=1 i ∡FCB = β. Oblicz pole trójkąta ABC.
Za zadania 1-3 maksymalną liczbę 30 pkt. uzyskali: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Sabina Sy (studentka III roku nanotechnologii, UJ Kraków). 28 pkt. zdobyli: Anna Gudełajtis (uczennica, II LO Opole) oraz Michel Migas (student, PW Warszawa). 26 pkt. zdobyli: Iwona Gruszecka (nauczycielka, G 28 Wrocław) i Krzysztof Sobków (nauczyciel, II LO Opole).
Za zadanie 4 maksymalną liczbę 10 pkt uzyskali: Jacek Bagiński, Włodzimierz Bąk, Michel Migas, Krzysztof Sobków, Sabina Sy, Tadeusz Porzucek (emeryt, Gostyń) i Arkadiusz Wróbel (Brwinów, student UW).
Gratulujemy!
Zadanie 1. Wystarczy pokazać, że punkty B i O należą do symetralnej odcinka MN. Ponieważ |OM|=|ON|=R, wystarczy wykazac, że BM ≡ BN. Oznaczmy miarę kąta DAB równoległoboku przez α. Wówczas |∡MNB|=|∡MAB|= α, bo są to kąty wpisane w okrąg oparte na łuku MB oraz analogicznie |∡NMB|=|∡NCB|= α. Zatem trójkąt BNM jest równoramienny (BN≡BM), co kończy dowód. Położenie punktu D nie ma wpływu na tok rozumowania.
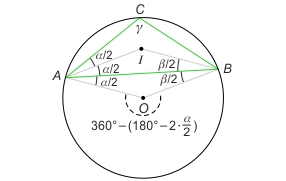
Zadanie 3. Dla ustalenia uwagi załóżmy, że środki okręgów wpisanego w trójkąt i opisanego na trójkącie są symetryczne względem boku AB. Oznacza to, że kąt γ przy wierzchołku C jest rozwarty. Wobec założenia mamy |∡DAB|=|∡BAI| = α/2 oraz |∡OAB|=|∡ABI| = β/2. Ale trójkąt AOB jest równoramienny, stąd α=β i trójkąt ABC też jest równoramienny. Kąt ACB jest wpisany w okrąg i jest połową kąta środkowego AOB opartego na tym samym łuku, czyli γ = 1/2 (360°-(180°-2·α/2) = 90°+α/2. Dalej z sumy kątów wewnętrznych w trójkącie ABC mamy
90°+α/2+2α = 180°, skąd α=36°. Zatem kąty w trójkącie ABC mają miary 36°, 36° i 108°.
Zadanie 4. Zasadniczy pomysł to obranie punktu S na srodku odcinka DE. Wówczas czworokąt FBES jest rombem. Zauważmy, że CS jest środkową trójkąta prostokątnego CDE, zatem |CS|=1. Oznacza to, że punkty F, E, C i D leżą na okręgu o środku S. Zauważmy dalej, że |∡ESF| = 2β, bo jest to kąt środkowy oparty na łuku EF. Ponieważ |∡ABC| = 2β i DE || AB, zachodzi |∡DEC| = 2β. W trójkącie prostokątnym CDE mamy więc |CE|=|DE|cos 2β = 2cos 2β, a w trójkącie ACB mamy |AC| = |BC|tg2β = (|CE|+1)tg2β = (2cosβ+1)tg2β.
Ostatecznie PΔABC = 1/2|AC|·|BC| = 1/2(2cos2β+1)2 tg2β.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
Pytanie o interpretację zadania 2
Czy okręgi o promieniach R i r są styczne zewnętrznie w punkcie K, czy przecinają się w dwóch punktach, z których jeden to K?
Odpowiedź
Okręgi przecinają się naprawdę.