Zad. 1. Prezent mikołajkowy zapakowano do sześciennego pudełka i oklejono wstążką. Rysunek przedstawia przebieg pętli wstążki na pudełku w rzucie na ścianę przednią, prawą boczną i górną. Zaznacz przebieg wstążki na sześcianie. W rozwiązaniu wystarczy przesłać załącznik z zeskanowanym odręcznym szkicem lub link do rysunku w http://sketchtoy.com .
Zad. 2. Ojciec i syn mieli wypadek samochodowy. Przyjechały dwie karetki. Pierwsza zabrała syna, gdyż ojciec utknął na kilka godzin we wraku. W chwilę później, w szpitalu chirurg, zobaczywszy chłopca, krzyknął: „Nie mogę operować, przecież to mój syn!”. Jak to możliwe?
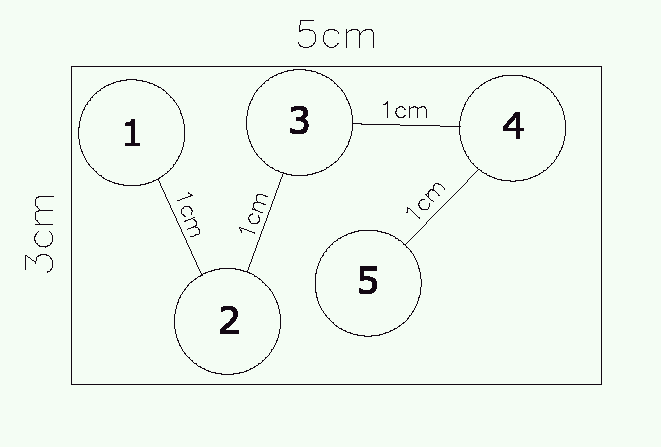
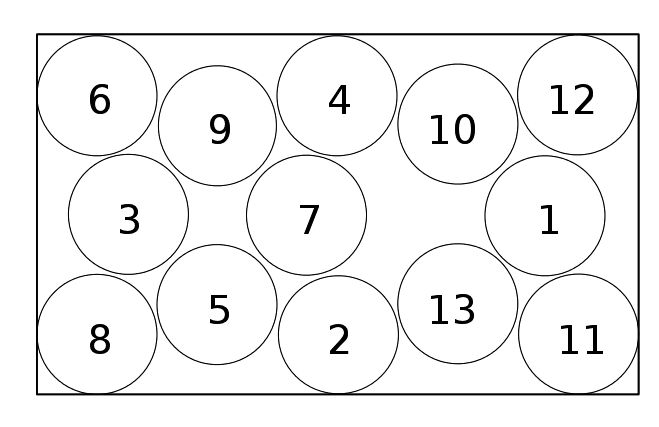
Zad. 3. Znajdź największą liczbę żetonów o średnicy 1 cm, które można umieścić w prostokącie o wymiarach 5 cm na 3 cm, postępując według podanego przepisu: pierwszy żeton możemy położyć w dowolnym miejscu, drugi - w odległości 1 cm od pierwszego, trzeci - w odległości 1 cm od drugiego itd. Żadne żetony nie mogą dotykać się wzajemnie i wszystkie muszą leżeć wewnątrz prostokąta. Odpowiedź należy zilustrować rysunkiem z ponumerowanymi żetonami. Poniższy rysunek przedstawia przykładowe rozmieszczenie według tej zasady 5 żetonów.
Zad. 1. Rozwiązanie przedstawia rysunek.
Zad. 2. Chirurg był kobietą (matką chłopca).
Zad. 3. Przykładowe rozmieszczenie żetonów przedstawia rysunek.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
Brzeg prostokąta
"Żadne żetony nie mogą dotykać się wzajemnie i wszystkie muszą leżeć wewnątrz prostokąta." Czy dopuszczalne jest, aby brzeg koła (żetonu) miał jakiś punkt wspólny z brzegiem prostokąta?
Odp.
Żetony to matematycznie koła. Koło zawiera swój brzeg. Skoro ma leżeć we wnętrzu prostokąta, to oczywiście razem z brzegiem.