Zad. 1. Rozwiąż nierówność [tex]\frac{x^2}{9+16x^4}\leq \frac{1}{24}[/tex].
Zad. 2. Ile jest różnych liczb pięciocyfrowych w systemie dwójkowym?
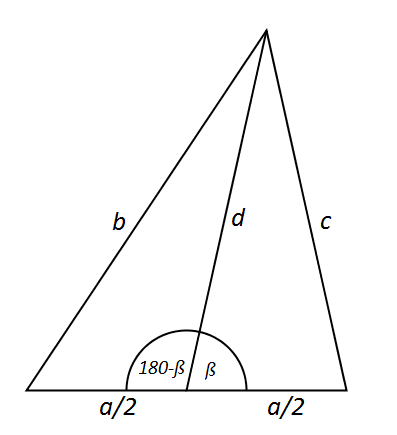
Zad. 3. Wyznacz długość środkowej trójkąta o bokach a, b, c opuszczonej na bok o długości a.
W grudniu punkty zdobyli:
- 3 - Szymon Bar PG 1 Głogówek, Bartłomiej Bychawski G Akademickie PWr, Gracjan Ciupa G 10 Wrocław, Jakub Dobrzański G 3 Lubin, Julia Grzyb G Wieliszew, Igor Hołowacz G Akademickie PWr, Jan Jancewicz G Akademickie PWr, Łukasz Janiak G Akademickie PWr, Alex Kalinowski G Dwujęzyczne Góra, Tomasz Lefler ZSS Wołów, Jakub Łojko SG Żary, Mikołaj Mastaliński G Akademickie PWr, Julia Mazur G Lewin Brzeski, Kacper Misiaczek G Akademickie PWr, Krzysztof Możdżeń ZSO 1 Żory, Krzysztof Nawrocki G Bóbrka, Krzysztof Nowak G Akademickie PWr, Magdalena Owczarek PZSO Legionowo, Michał Piórkowski G Urszulanek Wrocław, Małgorzata Plewka G Akademickie PWr, Maciej Płonka G Akademickie PWr, Jakub Rudzik G Akademickie PWr, Laura Stefanowska G im. Św. Franciszka z Asyżu Legnica, Paulina Szajer G Akademickie PWr, Michał Szwej G Dwujęzyczne Chorzów, Julia Waleńdzik PG 1 Brzeg Dolny i Patrycja Zakrzewska G Powiatowe Tuchola;
- 2 - Kacper Gembara ZSS Wołów, Mateusz Jankowski G 77 Warszawa, Nataniel Kędzierski G Akademickie PWr, Marek Komorowski ZS 3 Żory, Dawid Konieczko SG Szprotawa, Krzysztof Mach G 52 Kraków, Karolina Mielczarek G Lewin Brzeski, Jakub Musiała G Akademickie PWr, Krzysztof Palatyński G FILOMATA Gliwice, Katarzyna Penkalska G Wieliszew, Katarzyna Siomka G Lewin Brzeski, Piotr Strzeżyk G 1 Żory, Anna Tomala G 1 Żory, Mateusz Winiarski G Dwujęzyczne Krosno i Olga Zaborska PG 1 Ząbkowice Śląskie;
- 1,5 - Kosma Kasprzak G 58 Poznań, Kacper Kuszaj PG 2 Jelcz Laskowice i Karol Sadowski SG Żary;
- 1 -Weronika Klatka G Imielin i Kaja Srokosz G 58 Warszawa.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Po trzech miesiącach Gimnazjalnej Ligi Zadaniowej z wynikiem 9 pkt. (na 9 możliwych) prowadzą: Szymon Bar, Bartłomiej Bychawski, Julia Grzyb, Igor Hołowacz, Łukasz Janiak, Alex Kalinowski, Jakub Łojko, Julia Mazur, Kacper Misiaczek, Krzysztof Możdżeń, Krzysztof Nowak, Michał Piórkowski, Laura Stefanowska, Paulina Szajer, Michał Szwej i Julia Waleńdzik.
Drugie miejsce z wynikiem 8,5 pkt. zajmują: Jakub Dobrzański i Patrycja Zakrzewska.
Trzecie miejsce z wynikiem 8 pkt. zajmują: Gracjan Ciupa, Jan Jancewicz, Marek Komorowski, Mikołaj Mastaliński i Katarzyna Penkalska.
Gratulujemy!
Zad. 1. Ponieważ 9+16x4 > 0 to nierówność jest równoważna 24x2 ≤ 9+16x4.
Idąc dalej 0 ≤ 9+24x2+16x4, 0 ≤ (3+4x2)2.
Ta nierówność jest spełniona dla dowolnej liczby, czyli x jest liczbą rzeczywistą.
Zad. 2. Ponieważ liczba taka musi zaczynać się cyfrą 1 i następnie może na każdej z czterech pozycji przyjmować dowolną cyfrę 0 lub 1. Stąd takich liczb jest 1·24=16.
Zad. 3. Korzystając dwukrotnie z twierdzenia cosinusów dostaniemy
c2 = (a/2)2+d2-2·a/2·d·cos(β) i b2 = (a/2)2+d2-2·a/2·d·cos(180o-β).
Dodając stronami oba równania dostaniemy c2+b2 = 0,5·a2+2·d2,
czyli d = √(0,5·c2+0,5·b2-0,25·a2).
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
