Zad. 1. W ośmiokącie foremnym połączono przekątną dwa wierzchołki odległe o 3 (np. nr 1 z nr 4). Jaką częścią pola ośmiokąta jest pole utworzonego w ten sposób trapezu?
Zad. 2. Oblicz wartość poniższego wyrażenia, w którym w każdej liczbie występuje 2016 zer.
200...00162 – 200...0017 · 200...0015
Zad. 3. Funkcja f została zdefiniowana na zbiorze dodatnich liczb całkowitych i ma następujące własności:
1) f (xy) = f (x) + f (y) dla wszystkich liczb x i y
2) f (10) = 14
3) f (40) = 20
Ile wynosi f (500)?
W listopadzie punkty zdobyli:
- 3 - Szymon Bar G 1 Głogówek, Bartłomiej Bychawski G Akademickie PWr, Jakub Dobrzański G 3 Lubin, Kacper Gembara G w ZSS Wołów, Julia Grzyb G Wieliszew, Igor Hołowacz G Akademickie PWr, Damian Jagiełło G Akademickie PWr, Jan Jancewicz G Akademickie PWr, Łukasz Janiak G Akademickie PWr, Mateusz Jankowski G 77 Warszawa, Alex Kalinowski G Dwujęzyczne Góra, Kosma Kasprzak G 58 Poznań, Marek Komorowski G w ZS nr 3 Żory, Jakub Łojko SG Żary, Mikołaj Mastaliński G Akademickie PWr, Julia Mazur G Lewin Brzeski, Karolina Mielczarek G Lewin Brzeski, Kacper Misiaczek G Akademickie PWr, Krzysztof Możdżeń G w ZSO nr 1 Żory, Krzysztof Nawrocki G Bóbrka, Krzysztof Nowak G Akademickie PWr, Mateusz Padarz G Akademickie PWr, Krzysztof Palatyński G Filomata Gliwice, Katarzyna Penkalska G Wieliszew, Michał Piórkowski G Urszulanek Wrocław, Małgorzata Plewka G Akademickie PWr, Jakub Rudzik G Akademickie PWr, Michał Rzepka G 5 Głogów, Karol Sadowski SG Żary, Katarzyna Siomka G Lewin Brzeski, Kacper Słoniec G 52 Kraków, Kaja Srokosz G 58 Warszawa, Laura Stefanowska G św. Franciszka z Asyżu Legnica, Paulina Szajer G Akademickie PWr, Michał Szwej G Dwujęzyczne Chorzów, Julia Waleńdzik PG 1 Brzeg Dolny, Mateusz Winiarski G Dwujęzyczne Krosno, Olga Zaborska G 1 Ząbkowice Śląskie i Patrycja Zakrzewska G Powiatowe Tuchola;
- 2 - Dominik Bysiewicz G Dwujęzyczne Krosno, Dominik Chmielowiec G Trzebownisko, Gracjan Ciupa G 10 Wrocław, Nataniel Kędzierski G Akademickie PWr, Weronika Klatka G Imielin, Szymon Kowaliński G Akademickie PWr, Kacper Kuszaj G 2 Jelcz-Laskowice, Konrad Leszczyński G Akademickie PWr, Krzysztof Mach G 52 Kraków, Wojciech Rudziński G 1 Głubczyce, Gaspar Sekula G Akademickie PWr i Julian Wach G Akademickie PWr;
- 1 -Tomasz Lefler G w ZSS Wołów, Jakub Musiała G Akademickie PWr, Maciej Płonka G Akademickie PWr, Sylwia Polak G Trzebownisko, Piotr Strzeżyk G 1 Żory i Anna Tomala G 1 Żory.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Po dwóch miesiącach Gimnazjalnej Ligi Zadaniowej z wynikiem 6 pkt. (na 6 możliwych) prowadzą: Szymon Bar, Bartłomiej Bychawski, Julia Grzyb, Igor Hołowacz, Łukasz Janiak, Alex Kalinowski, Kosma Kasprzak, Marek Komorowski, Jakub Łojko, Julia Mazur, Kacper Misiaczek, Krzysztof Możdżeń, Krzysztof Nowak, Katarzyna Penkalska, Michał Piórkowski, Michał Rzepka, Karol Sadowski, Kaja Srokosz, Laura Stefanowska, Paulina Szajer, Michał Szwej i Julia Waleńdzik.
Drugie miejsce z wynikiem 5,5 pkt. zajmują: Jakub Dobrzański, Kacper Gembara, Mateusz Jankowski i Patrycja Zakrzewska.
Trzecie miejsce z wynikiem 5 pkt. zajmują: Dominik Bysiewicz, Gracjan Ciupa, Jan Jancewicz i Mikołaj Mastaliński.
Gratulujemy!
Zad. 1. Pole tego trapezu stanowi 1/4 pola ośmiokąta, co łatwo widać z poniższego rysunku.
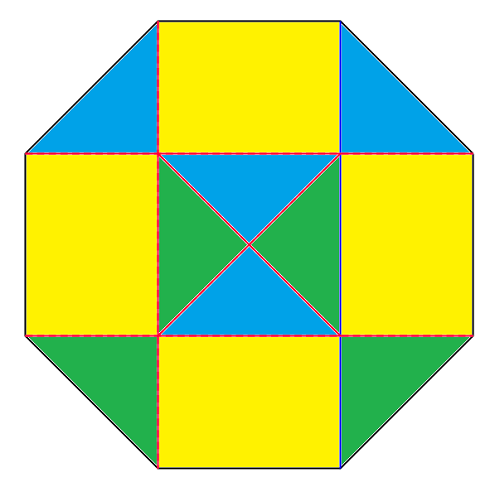
Zad. 2. Niech x = 200...0016. Wtedy 200...00162 – 200...0017·200...0015 = x2 – (x+1)(x–1) = 1.
Zad. 3. Zauważmy, że 20 = f (40) = f (5·2·2·2) = f (5)+3·f (2) oraz 14 = f (10) = f (5·2) = f (5)+f (2).
Rozwiązując ten układ równań, dostaniemy f (5) = 11 i f (2) = 3.
Stąd f (500) = f (5·5·5·2·2) = 3·f (5)+2·f (2) = 33+6 = 39.







