Zad. 1. W pewnej loterii losy wygrywające mają numery, których cyfry można podzielić na dwie grupy tak, aby sumy cyfr w każdej z grup były jednakowe. Znajdź najmniejszą liczbę naturalną a taką, że losy o numerach a i a+1 są wygrywające.
Zad. 2. Dane są trzy jednakowe okręgi parami styczne. Pomiędzy nimi znajduje się mniejszy okrąg styczny do każdego z nich. Jaki jest stosunek promieni mniejszego do większego okręgu?
Zad. 3. Wypisujemy kolejne liczby naturalne, otrzymując ciąg cyfr 123456789101112131415... Jaka cyfra znajduje się na 2019. miejscu tego ciągu?
W grudniu punkty zdobyli:
- 3 pkt. – Adrian Chudzik I LO Leszno, Dominik Bysiewicz I LO Krosno, Dominika Horodecka KLO Gdynia, Bartosz Kaczor I LO Głogów, Laura Stefanowska KLO Legnica, Aleksandra Strzelecka VIII LO Poznań, Wojciech Szwarczyński II LO Wałbrzych; Igor Wojtun I LO Głogów, Gabriela Wołynko I LO Węgrów, Kacper Woszczek II LO Wałbrzych,
- 2 pkt. – Karol Czub LO2 Oleśnica, Konrad Leszczyński XIV LO Wrocław, Wiktoria Malinowska XXVII LO Warszawa, Natalia Siwek II LO Poznań, Roman Szlachtun LO 9 Wrocław;
- 1 pkt. – Szymon Kowalcze ZSE Brzeg, Kasper Radom II LO Lubin.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Numery losów muszą być co najmniej dwucyfrowe, aby jego cyfry można było podzielić na dwie grupy. Suma cyfr numeru, który wygrywa, składa się z dwóch jednakowych składników, więc jest liczbą parzystą. Dwie kolejne liczby a i a+1 mają parzystą sumę cyfr tylko wtedy, gdy a kończy się cyfrą 9 (dlaczego?). Z liczb dwucyfrowych jedyne możliwe a to 99, a wśród trzycyfrowych mogą to być liczby, których suma cyfr wynosi 18 (może być też większa, ale szukamy najmniejszego możliwego przykładu). Dobrymi liczbami a mogą więc być: 99, 189, 279, 369, 459, ale ich następniki a+1 (czyli 100, 190, 280, 370 i 450) nie spełniają warunku numeru wygrywającego. Najmniejszą dobrą parą jest 549 i 550, bo [tex]\underbrace{54}_{9}\underbrace{9}_{9}[/tex] oraz [tex]\underbrace{5}_{50}\underbrace{5}_{5}[/tex], czyli najmniejsze możliwe a to 549.
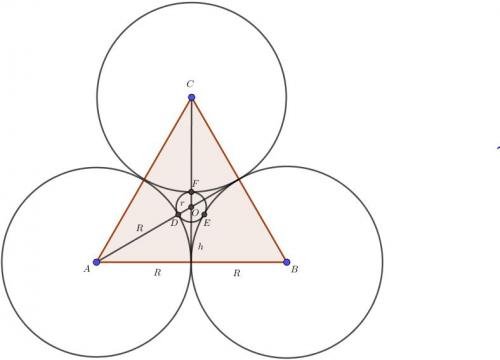
Zad. 2. Na poniższym rysunku |OD| = |OE| = |OF| = r oraz |OA| = |OB| = |OC| = R. Trójkąt ABC jest równoboczny i |AB| = |BC| = |CA| = 2R. Punkt O jest miejscem przecięcia wysokości trójkąta (tzw. ortocentrum). Zachodzi 2/3h = r+R oraz h = 2R√3/2 = R√3. Podstawiając za h, mamy R+r = 2/3R√3, a po przekształceniu r/R = 2√3-3/3.
Zad. 3. W ciągu 123456789101112131415... dziewięć miejsc zajmują liczby jednocyfrowe (1, 2, 3, …, 9), dalszych 180 miejsc zajmuje 90 liczb dwucyfrowych (10, 11, 12, …, 99). Razem daje to 189 miejsc. Pozostaje 2019 – 189 = 1830 miejsc. Szukana cyfra stoi więc na 1830 miejscu w ciągu kolejnych liczb trzycyfrowych. Ponieważ 1830 : 3 = 610, jest to ostatnia cyfra 610. liczby trzycyfrowej. Tą liczbą jest 100 + 609 = 709, zatem na 2019. miejscu w ciągu znajduje się cyfra 9.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
