Zad. 1. Dwadzieścia osób, pracując w równym tempie, miało wykonać pewną pracę w ciągu 10 godzin. Wszyscy pracowali przez 6 godzin, po czym 10 osób opuściło stanowiska pracy. O ile wydłużył się czas wykonania pracy, jeśli pozostałe 10 osób pracowało do końca?
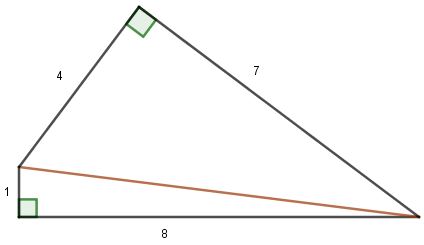
Zad. 2. Jakie największe pole może mieć czworokąt, którego boki mają długości 1, 4, 7, 8?
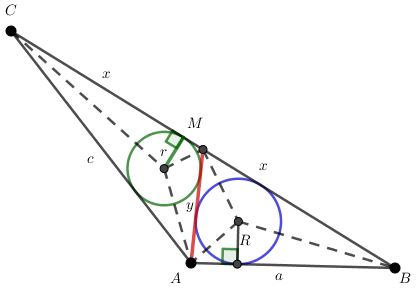
Zad. 3. W trójkącie ABC poprowadzono środkową AM. Czy promień okręgu wpisanego w trójkąt ABM może być dwa razy większy od promienia okręgu wpisanego w trójkąt ACM? Odpowiedź uzasadnij.
W styczniu punkty zdobyli:
- 3 pkt. – Dominik Bysiewicz I LO Krosno, Bartosz Kaczor I LO Głogów, Wiktoria Malinowska XXVII LO Warszawa, Laura Stefanowska KLO Legnica, Kasper Radom II LO Lubin, Aleksandra Strzelecka VIII LO Poznań, Wojciech Szwarczyński II LO Wałbrzych, Igor Wojtun I LO Głogów, Kacper Woszczek II LO Wałbrzych,
- 2 pkt. – Adrian Chudzik I LO Leszno, Karol Czub II LO Oleśnica, Mikołaj Mosiak II LO Oleśnica, Szymon Narolski II LO Oleśnica, Roman Szlachtun LO 9 Wrocław;
- 1 pkt. – Gabriela Wołynko I LO Węgrów.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Po 6 godzinach 10 pracowników opuściło stanowiska pracy. W pełnym składzie pracowaliby jeszcze przez 4 godziny. Ponieważ zostało dwa razy mniej pracowników, pozostałą pracę wykonają w czasie dwa razy dłuższym, czyli w 8 godzin. Czas pracy wydłużył się zatem o 4 godziny.
Zad. 2. Przekątna czworokąta dzieli go na dwa trójkąty. Wśród wszystkich trójkątów o bokach długości a i b największe pole ma trójkąt prostokątny o przyprostokątnych a i b (bo w przeciwnym wypadku wysokość trójkąta opuszczona na jeden z tych boków byłaby mniejsza od drugiego boku, zatem i pole trójkąta byłoby mniejsze). Dla liczb 1, 4, 7, 8 zachodzą równości 12+82 = 65 i 42+72 = 65, zatem kąty proste zawarte są między bokami 1 i 8 oraz 4 i 7. Pole tego czworokąta wynosi 18.
Zad. 3. Środkowa AM dzieli trójkąt ABC na dwa trójkąty ABM i AMC o równych polach. Oznaczmy przez R promień okręgu wpisanego w trójkąt ABM, przez r – promień okręgu wpisanego w trójkąt AMC oraz niech |AB|=a, |BM|=|MC|=x, |AM|=y i |CA|=c. Wówczas ½ R(a+x+y) = ½ r(y+x+c). Jeśli R=2r, to po podstawieniu do równania i przekształceniu otrzymujemy c = 2a+x+y, ale na podstawie nierówności trójkąta c < x+y, zatem otrzymujemy sprzeczność. Promień okręgu wpisanego w trójkąt ABM nie może być dwa razy większy od promienia okręgu wpisanego w trójkąt ACM.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
