Zad. 1. Czy jakiś trójkąt rozwartokątny da się pokroić na skończenie wiele kawałków, z których każdy jest trójkątem ostrokątnym?
Zad. 2. Wykaż, że kwadrat sumy n poczatkowych liczb naturalnych jest równy sumie sześcianów tych liczb.
Zad. 3. Czy istnieje ciąg liczb rzeczywistych, w którym a1=1 oraz (an+1 – an)2 = an+1 + an?
W tym miesiącu punkty otrzymał:
- 12 - Aleksander Porębny (SP 113 Wrocław).
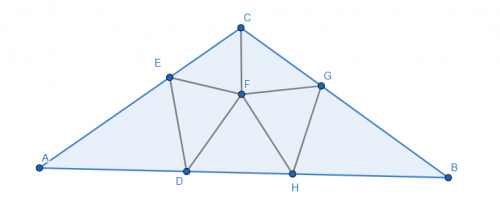
Zad. 1. Należy „odkroić” dwa wierzchołki trójkąta i podzielić powstały pięciokąt na pięć trójkątów ostrokątnych.
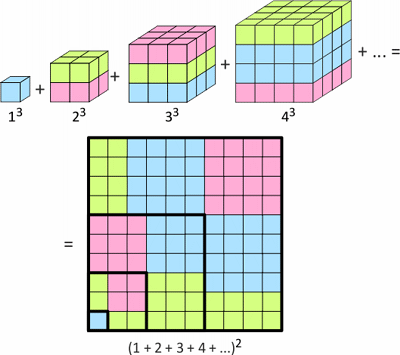
Zad. 2. Najprościej przeprowadzić dowód, używając indukcji matematycznej. Twierdzenie to można także wykazać w sposób bardziej estetyczny. Uczestnik OMJ powinien dać sobie radę ze zrozumieniem przynajmniej jednego dowodu z tej strony internetowej. Można też przeprowadzić dowód geometryczny (rysunek poniżej). Uzasadnij jego poprawność.
Zad. 3. Ciąg jedynek i zer ułożonych naprzemiennie spełnia warunki zadania. Warto pokusić się o próbę wyznaczenia wszystkich takich ciągów!
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
