Zad. 1. Dla jakich liczb naturalnych n spełniona jest poniższa równość?
(-1)1+(-1)2+(-1)3+…+(-1)n = (-1)1·(-1)2·(-1)3· ... ·(-1)n
Zad. 2. Znajdź wszystkie liczby naturalne x spełniające warunek x:2008 ≈ 200,8, gdzie liczba po prawej stronie jest zaokrągleniem dokładnego wyniku do części dziesiątych. Ile jest takich liczb?
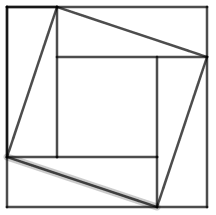
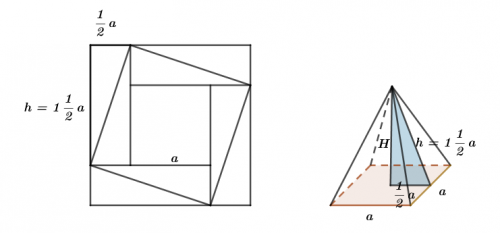
Zad. 3. Kwadrat o boku 12 rozcięto na mniejszy kwadrat i 8 jednakowych trójkątów prostokątnych tak jak na rysunku poniżej. Ze wszystkich tych elementów zbudowano siatkę ostrosłupa prawidłowego czworokątnego. Oblicz jego objętość.
W kwietniu punkty zdobyli:
- 3 – Natalia Czurejno SP Wykroty, Łukasz Dukiel SP 16 Wrocław, Mateusz Galik SP Arka Wrocław, Igor Gawrzoł, SP Aslan Głogów, Rafał Frankowski SP 139 Warszawa, Wiktor Kuczaj SP 7 Nowa Ruda, Aleksander Masztalski SP 3 Mikołów, Krzysztof Pajek SP 50 Wrocław, Wiktoria Pietrzak SP 3 Głogów, Gabriela Pułecka SP 2 Brzeg Dolny, Oliwia Stańczyk SP Aslan Głogów;
- 2,5 – Anastasia Yakovleva SP 3 Mogilno;
- 2 – Martyna Burnos SP 3 Głogów, Julia Kałużny SP 3 Głogów, Aleksandra Koziej SP Jarczew, Joanna Nowakowska SP 3 Głogów, Arkadiusz Piwowarczyk SP 14 Ostrowiec Świętokrzyski, Adrian Przygodzki SP Strzelce, Oliwia Raszewska SP 6 Boguszów-Gorce, Julia Strzelecka SP 50 Wrocław, Dominika Wojdacz SP 11 Inowrocław;
- 1,5 – Anna Janczyńska SP 26 Kraków, Oliwia Ryndak SP 26 Kraków, Szymon Ryś SP 16 Wrocław.
- 1 - Maja Dałek SP 44 Wrocław, Tymon Ryniejski SP 50 Wrocław, Tytus Szczapa SP Młody Kopernik Wałbrzych, Juliusz Tarczyński SP 64 Wrocław.
Zad. 1. Kolejne składniki z lewej strony równości są równe na przemian -1 i 1, więc dla kolejnych liczb naturalnych n lewa strona przyjmuje wartość -1 dla n nieparzystego oraz 0 dla n parzystego. Obliczając wartości prawej strony dla kolejnych liczb naturalnych n, otrzymujemy: -1, -1, 1, 1, -1, -1, 1, 1, … . Równość będzie spełniona, gdy obie strony będą przyjmowały wartość -1, czyli dla n równych 1, 5, 9 itd, czyli dla n dających resztę 1 z dzielenia przez 4 (tzn. n=4k+1, gdzie k jest liczbą naturalną).
Zad. 2. Warunek z zadania można opisać nierównością: 200,75 ≤ x:208 < 200,85. Ponieważ 200,75.2008 = 403106 i 208,85.2008 = 403306,8, otrzymujemy 403106 ≤ x < 403306,8. Wszystkie liczby naturalne spełniające ten warunek to: 403106, 403107, 403108, …, 403306. Tych liczb jest 403306–403105=201.
Zad. 3. Oznaczmy długość boku mniejszego kwadratu przez a. Wówczas przyprostokątne trójkątów wynoszą 0,5a i 1,5a, a duży kwadrat będzie ma bokdługości 2a. Ponieważ 2a = 12, więc a = 6. Podstawą ostrosłupa jest kwadrat o boku a, a ścianą boczną - trójkąt równoramienny o podstawie a i wysokości h = 1,5a. Wysokość H ostrosłupa można wyliczyć z twierdzenia Pitagorasa (dla jakiego trójkąta?): H2+(0,5a)2 = (1,5a)2, czyli H2+32 = 92. Stąd h=6√2, a objętość ostrosłupa wynosi 1/3a2·H = 1/3·36·6√2 = 72√2 cm3.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
