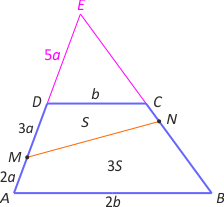
Zad. 1. Na ramieniu AD trapezu ABCD obrano punkt M taki, że |AM|:|MD| = 2:3, a na ramieniu BC - punkt N taki, że odcinek MN dzieli trapez na dwie części, z których jedna ma pole trzy razy większe niż druga. Wiedząc że|DC|:|AB| = 1:2, oblicz stosunek |CN|:|NB|.
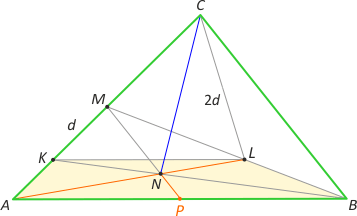
Zad. 2. Niech M będzie środkiem boku AC trójkąta ABC. Na odcinkach AM, BM i BK obrano odpowiednio punkty K, L i N, przy czym odcinek KL jest równoległy do AB, odcinek MN jest równoległy do BC, a |CL| = 2·|KM|. Wykaż, że CN jest dwusieczną kąta ACL.
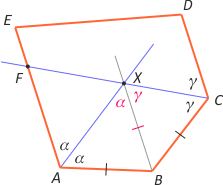
Zad. 3. W wypukłym pięciokącie ABCDE boki AE i CD są równoległe oraz |AB| = |BC|. Dwusieczne kątów A i C przecinają się w punkcie K. Wykaż, że odcinki BK i AE są równoległe.
Zad. 4. (wolna amerykanka) W czworokącie ABCD odcinki AB i AD mają równe długosci, a kąty ABC i ADC są proste. Na bokach BC i CD obrano odpowiednio punkty F i E takie, że odcinki DF i AE są prostopadłe. Wykaż, że prostopadłe są też odcinki AF i BE.
W tym miesiącu za zadania 1-3 po 30 pkt. otrzymali:
Dominik Bysiewicz (student matematyki na UJ), Robert Ciężabka (korepetytor, Osiek Jasielski), Radosław Górzyński (uczeń I LO Lubin), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia) oraz Marzena Wąsiewicz (nauczycielka z Kajetan).
Za zadanie 4 po 10 pkt. otrzymali:
Dominik Bysiewicz, Robert Ciężabka, Radosław Górzyński, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek oraz Tadeusz Porzucek.
Gratulacje!
Zad. 1. Przedłużmy boki AD i BC do przecięcia się w punkcie E. Z podobieństwa trójkątów ABE i DCE w skali k = |AB|:|DC|= 2 wynika, że odcinek DC jest linią środkową w trójkącie ABE. Mamy zatem |DE|=5a. Przyjmijmy, że PMNCD = PABNM/3. Zauwazmy, że PDCE = PABE/4 = (PDCE + 4S)/4, skąd PDCE = 4S/3. Dalej PMNE/PABE = (7S/3)/(16S/3) = 7/16 = (|EM|·|EN|)/(|AE|·|BE|), bo kąt przy wierzchołku E jest wspólny dla obu trójkątów. Z kolei |EM|/|AE| = 8a/10a = 4/5, skąd otrzymujemy |EN|/|BE| = 35/64. Szukany stosunek |CN|/|NB| = (|EN|–|EC|)/|NB| =
|EN|/|NB|–|EC|/|NB| = |EN|/(|EB|–|EN|) – |EC|/(|EB|–|EN|) =
1/((|EB|/|EN|)–1) – 1/((|EB|/|EC|)–(|EN|/|EC|)) = 35/29 – 1/(2–(|EN|/(|BE|/2))) =
35/29 – 1/(2–35/32) = 3/29. Przyjęcie założenia, że PABNM = PMNCD/3 prowadzi zatem do sprzeczności.
Zad. 2. Przedłużmy odcinek MN do przecięcia się z bokiem AB w punkcie P. MP jest linią środkową w trójkącie ABC, a P jest środkiem boku BC. Rozważmy trapez ABLK. W punkcie M przecinają się przedłużenia boków AK i BL. Oznacza to, że prosta MP przechodzi przez środki podstaw i punkt przecięcia przekątnych (patrz zadanie 2 z października 2018), a tym samym, że punkt N leży na przekątnej AL. Zauważmy podobieństwo par trójkątów ABN z KNL oraz ABM z KLM. Otrzymujemy proporcję |AN|:|NL| = |AB|:|KL| = |AM|:|KM| = 2|AM|/2|KM| = |AC|/|CL|, skąd wynika, że CN jest dwusieczną kąta ACL.
Zad. 3. Niech prosta równoległa do AE przechodząca przez punkt B przecina odcinek CF w punkcie X. Zauważmy, że otrzymujemy dwa trójkąty równoramienne skąd wynika, że AX jest dwusieczną kąta A i punkt X pokrywa się z punktem K.
Zad. 4. (wolna amerykanka) Zapis pogrubiony oznacza wektor. Skorzystamy z iloczynu skalarnego wektorów. Z założenia mamy DF•AE = (-a+b+d)•(a+c) = -a•(a+c) + (b+d)•(a+c) = -a2–a•c+(b+d)•(a+c) = -a2+(b+d)•(a+c) = 0 skąd (b+d)•(a+c) = a2. Z kolei AF•BE = (b+d)•(a+c–b) = (b+d)•(a+c)–(b+d)•b = a2–b2–b•d = 0, co kończy dowód.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
