Zad. 1. Na tablicy korkowej w szkole są przyczepiane ogłoszenia na kartkach formatu A4. Każda kartka jest przyczepiona za pomocą 4 pinezek, jednak każda pinezka może przytrzymywać kilka sąsiednich kartek. Ile co najmniej pinezek należy użyć, aby przyczepić 25 kartek z ogłoszeniami?
Zad. 2. Na ile sposobów można podzielić tarczę zegara na cztery części, aby sumy liczb występujących w każdej z tych części były kolejnymi liczbami? Zaprezentuj te podziały. Wystarczy zrobić rysunek odręczny, zeskanować lub zrobić jego zdjęcie i przysłać jako załącznik.
Zad. 3. Ile jest liczb dwucyfrowych, które mają największą liczbę dzielników?
W listopadzie punkty zdobyli:
- 3 - Konrad Andruchów SP 4 Bolesławiec, Zuzanna Bar SP Twardawa, Bartłomiej Baranowski SP 6 Sieradz, Jakub Bartłomowicz SP 6 Jelenia Góra, Martyna Bielak SP Słomniki, Mikołaj Bilski SP 6 Jelenia Góra, Paweł Borzyszkowski SP Swornegacie, Michał Dolata SP 4 Warszawa, Krzysztof Drab SP 3 Mysłowice, Michał Dźwigaj SP 1 Przemków, Kornelia Ejsmont SP 28 Wałbrzych, Kamil Faryński SP 11 Inowrocław, Marcin Faryński SP 11 Inowrocław, Maja Frankowska SP 3 Lubin, Anna Gajewska SP Mieroszów, Szymon Grech SP Koszarawa Bystra, Maja Hofman SP Nowa Iwiczna, Michalina Hołowacz SP Bielany Wrocławskie, Aleksandra Janusz SP 293 Warszawa, Mateusz Jaroszewicz SP Academos Kraków, Ewa Jarża Polsko-Niemiecka SP Wrocław, Adrian Jastrzębski SP 10 Siedlce, Paulina Jeżewska SP Swornegacie, Magdalena Kaczmarska SP 63 Wrocław, Bartosz Krawczyk SP 4 Warszawa, Ewa Król SP Bielany Wrocławskie, Natalia Krystkiewicz KSP Mława, Kacper Kuchcik SP 11 Inowrocław, Dariusz Marszałek SP 1 Brzeg, Paweł Mieszkowski SP 52 Warszawa, Marek Molitorys KSP Katowice, Hanna Nadolna SP Swornegacie, Emilia Nowik SP 1 Sokółka, Aleksandra Olczyk SP 3 Środa Śląska, Julia Pawicka SP Bielany Wrocławskie, Adam Piotrowski KSP Mława, Szymon Podobiński SP Academos Kraków, Jakub Ptak SP 64 Wrocław, Kinga Ryska KSP Mława, Vanessa Siwy SP Twardawa, Marek Spychała SP 4 Warszawa, Adam Stachelek SP 301 Warszawa, Jerzy Wąsiewicz SP Kostowiec, Urszula Wąsiewicz SP Kostowiec i Dagmara Wroniszewska KSP Mława,
- 2,5 - Aleksandra Feliszek SP 63 Wrocław, Maciej Hibner SP 80 Warszawa, Agata Lefler SP 1 Wołów, Agata Misiak SP 52 Warszawa, Lena Nowacka SP 28 Wałbrzych, Aleksandra Sznajder SP 4 Warszawa i Weronika Świetlik SP Gostycyn;
- 2 - Aleksander Bury SP 63 Wrocław, Adam Chowanek SP Mieroszów, Oliwia Dąbrowska SP Żórawina, Sylwia Gregorczuk SP Bukowice, Oliwia Kupczyk SP Swornegacie, Hubert Kurek SP 2 Wrocław, Dominik Madejski SP 52 Warszawa, Jarosław Makówka SP 16 Studzienice, Matylda Mazurkiewicz SP Żórawina, Tymoteusz Noremberg SP 63 Wrocław, Weronika Przewłocka SP Mieroszów, Szymon Sadza SP 3 Ścinawa, Zuzanna Sojak SP Krasne, Tymon Srokosz SP 52 Warszawa, Grzegorz Swęd SP 31 Warszawa, Jan Swęd SP 31 Warszawa, Wiktoria Szkudlarek SP 107 Wrocław, Wojciech Szwarczyński SP Kowalowa, Marta Tarnogrodzka SP Żórawina, Miłosz Truszkowski SP 1 Żuromin, Aleksandra Tylman SP 3 Ścinawa, Franciszek Urbaniak SP 1 Łomianki, Jan Wiktorzak SP 23 Radom, Jakub Wojnarowicz SP 2 Wrocław, Kacper Woszczek SP Mieroszów i Wojciech Zawiślak SP 2 Kręty,
- 1,5 - Maja Kądziela SP Academos Kraków, Marcel Matysiak SP 1 Góra, Dawid Sitarz SP Żórawina, Antoni Skomorowski SP Bielany Wrocławskie i Natalia Waśko SP 4 Warszawa,
- 1 - Hubert Błonowski SP Stary Karszew, Natalia Dybek SP Stary Karszew, Dawid Jaworski SP Żórawina, Bartłomiej Kaczor SP 52 Warszawa, Lothar Kroekel SP 63 Wrocław, Bartosz Kuriata SP Żórawina, Kacper Momot SP Żórawina, Agata Niemiec SP 28 Wałbrzych, Bartosz Orlikowski SP 10 Wrocław, Mateusz Rabenda SP 63 Wrocław, Natalia Rabenda SP 63 Wrocław, Tomasz Rzymkowski SP 10 Gdynia, Karol Wieczorek SP Żórawina, Elżbieta Wójcik SP Piotrów i Yulian Zhydachevskyy SP 191 Warszawa,
- 0,5 - Aleksandra Maredyk SP 7 Mława.
Pozostali uczestnicy otrzymali poniżej 0,5 punktu.
Po dwóch miesiącach Ligi Zadaniowej dla SP z wynikiem 6 pkt. (na 6 możliwych) prowadzą: Konrad Andruchów, Zuzanna Bar, Jakub Bartłomowicz, Martyna Bielak, Mikołaj Bilski, Paweł Borzyszkowski, Michał Dolata, Michał Dźwigaj, Kamil Faryński, Marcin Faryński, Maja Frankowska, Anna Gajewska, Szymon Grech, Maja Hofman, Michalina Hołowacz, Aleksandra Janusz, Mateusz Jaroszewicz, Adrian Jastrzębski, Magdalena Kaczmarska, Bartosz Krawczyk, Ewa Król, Natalia Krystkiewicz, Kacper Kuchcik, Dariusz Marszałek, Paweł Mieszkowski, Marek Molitorys, Hanna Nadolna, Emilia Nowik, Aleksandra Olczyk, Julia Pawicka, Adam Piotrowski, Jakub Ptak, Kinga Ryska, Vanessa Siwy, Adam Stachelek, Jerzy Wąsiewicz, Urszula Wąsiewicz i Dagmara Wroniszewska.
Drugie miejsce z wynikiem 5,5 pkt. zajmują: Aleksandra Feliszek, Maciej Hibner, Agata Misiak, Lena Nowacka, Aleksandra Sznajder i Weronika Świetlik,
Trzecie miejsce z wynikiem 5 pkt. zajmują: Aleksander Bury, Oliwia Dąbrowska, Krzysztof Drab, Kornelia Ejsmont, Paulina Jeżewska, Matylda Mazurkiewicz, Tymoteusz Noremberg, Szymon Podobiński, Szymon Sadza, Zuzanna Sojak, Tymon Srokosz, Grzegorz Swęd, Miłosz Truszkowski, Aleksandra Tylman, Franciszek Urbaniak, Jakub Wojnarowicz i Kacper Woszczek.
Gratulujemy!
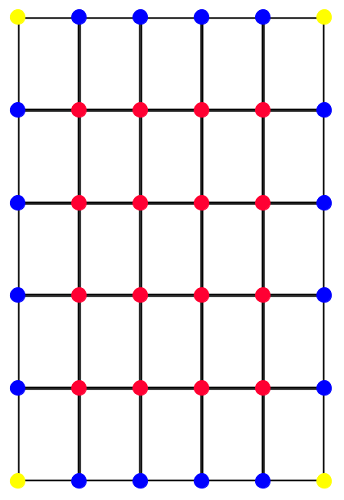
Zad. 1. Należy użyć co najmniej 36 pinezek, a kartki ustawić w "kawdrat" 6×6". Na poniższym rysunku pinezki czerwone przytrzymują po 4 kartki, niebieskie po 2, a żółte po 1.
Zad. 2. Suma liczb na tarczy zegara to 78. Dzieląc ją na 4 dostajemy 19,5. Z tego wynika, że cztery kolejne liczby będące sumami godzin to 18, 19, 20 i 21. Zadanie to ma jedno rozwiązanie przy założeniu, że godziny są rozmieszczone na obwodzie tarczy zegara. Stosowny podział przedstawia poniższy rysunek.
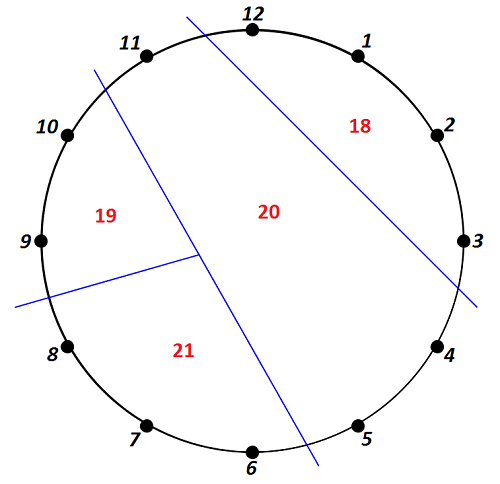
Powyższe rozwiązanie działa dla każdego modelu zegara i takie rozwiązania uznawaliśmy za poprawne.
Jeśliby przyjąć, że mamy taki cyferblat, na którym godziny leżą wewnątrz tarczy, zadanie staje się znacznie trudniejsze. Wtedy podziałów spełniających warunki zadania jest 901. Wszystkich podziałów zbioru 12 liczb na 4 niepuste podzbiory jest 611501. Jeśli te podzbiory mają dawać sumy 18, 19, 20 i 21, pewne kombinacje można z góry odrzucić (np. podział na trzy podzbiory jednoelementowe i jeden 9-elementowy). Interesujące nas podziały mają następujące liczności elementów:
- {6, 2, 2, 2}, co daje 13860 możliwości, ale tylko 2 przypadki dają żądane sumy,
- {5, 3, 2, 2}, co daje 83160 możliwości, ale tylko 86 przypadków daje żądane sumy,
- {4, 4, 2, 2}, co daje 51975 możliwości, ale tylko 84 przypadki dają żądane sumy,
- {4, 3, 3, 2}, co daje 138600 możliwości, ale tylko 578 przypadków daje żądane sumy,
- {3, 3, 3, 3}, co daje 15400 możliwości, ale tylko 151 przypadków daje żądane sumy.
Zatem z 302995 rozpatrywanych podziałów tylko 901 daje właściwe sumy podzbiorów. Sprawdzenie tego w rozsądnym czasie wymaga użycia komputera.
Zad. 3. Szukanych liczb jest 5. Wszystkie mają 12 dzielników. Są to 60 = 22·3·5, 72 = 23·32, 84 = 22·3·7, 90 = 2·32·5 i 96 = 25·3. Aby łatwo znaleźć ilość wszystkich dzielników danej liczby, rozkładamy ją na czynniki pierwsze, a następnie tworzymy konkretny dzielnik, wybierając do niego dany czynnik pierwszy w każdej z możliwych potęg od 0 (wtedy de facto nie wybieramy go do dzielnika), aż do tej potęgi, w jakiej występuje on w liczbie. Na przykład dla liczby 60 do dzielnika można wybrać dwójkę na 3 sposoby (20, 21 i 22), a trójkę i piątkę na 2 sposoby. Ponieważ czynniki pierwsze wybieramy niezależnie, liczba możliwych do utworzenia dzielnikow jest iloczynem wykładników powiększonych o 1 i np. dla liczby 60 wynosi 3·2·2 = 12.




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Pytanie do zad. 2.
Jakie liczby są widoczne na tarczy zegara: czy tylko godzinowe, czy tylko minutowe, czy godzinowe i (jednocześnie) minutowe?
Odp.
Chodzi o tarczę zegara analogowego (ze wskazówkami). Na takich zegarach podpisane są tylko godziny.
Zadanie z podziałami
Zadanie nieprecyzyjnie określa przebieg linii podziału tarczy. Proszę doprecyzować. Z tekstu nie wynika, czy linie podziału to proste, czy łamane, czy dowolne linie. Czy linie podziału, jeśli są dowolnymi liniami, mogą przebiegać pomiędzy okręgiem tarczy a cyframi do zapisu numeru godzin?
Zadanie z podziałami
Zgadzam się. W zadaniu nie jest powiedziane, że dzielić tarczę zegara mają proste. Można zatem wnioskować, że mogą to być dowolne linie łamane albo nawet krzywe. Sprawdziłem na komputerze: jest dokładnie 901 możliwości pocięcia tarczy nożyczkami, tak żeby każdy z 4 obszarów pozostał spójny. "Wystarczy zrobić rysunek odręczny, zeskanować lub zrobić jego zdjęcie i przysłać jako załącznik" - Mam przesłać 901 rysunków? Czasem mam wrażenie, że te zadania układają humaniści...
Podział tarczy
W zadaniu nie ma założenia, że linie podziału mają być prostymi, więc prostymi być nie muszą. Ich kształt w ogóle nie ma znaczenia. Ważne żeby tarcza zegara rozpadła się na 4 części. Takich linii dzielących (dla tego samego układu godzin na każdej z części) jest nieskończenie wiele. Nie chodzi przecież o to, żeby zliczać sposoby poprowadzenia linii, bo to nie ma sensu. Należy zliczać sposoby podziału tarczy na cztery części różniące się układem godzin.
Do Tomasza
Tomaszu! Czyżbyś sugerował, że humanista jest synonimem człowieka bezmyślnego? Jeśli tak, to proszę, nie używaj słów, których znaczenia nie rozumiesz. Inteligentni ludzie tak nie robią. Sam piszesz zupełnie bezmyślne rzeczy, Twoja odpowiedź nie ma sensu. Na szczęście dla uczestników ligi, którym popsułbyś swoim niemądrym wpisem zabawę.
@redakcja
Tak, ja twierdze, że podziałów różniących się układem godzin jest 901. Proszę wybrać dowolny z nich a ja dostarczę rysunek z podziałem. Każdy z 4 obszarów będzie spójny.
9,12|1,8,11|2,7,10|3,4,5,6
9,12|1,8,11|3,6,10|2,4,5,7
9,12|1,8,11|4,5,10|2,3,6,7
9,12|1,8,11|2,3,4,10|5,6,7
9,12|2,7,11|1,8,10|3,4,5,6
9,12|3,6,11|1,8,10|2,4,5,7
9,12|4,5,11|1,8,10|2,3,6,7
9,12|2,3,4,11|1,8,10|5,6,7
9,12|2,7,11|3,6,10|1,4,5,8
9,12|2,7,11|4,5,10|1,3,6,8
9,12|2,7,11|1,3,5,10|4,6,8
9,12|3,6,11|2,7,10|1,4,5,8
9,12|4,5,11|2,7,10|1,3,6,8
9,12|1,3,5,11|2,7,10|4,6,8
9,12|3,6,11|4,5,10|1,2,7,8
9,12|1,2,6,11|4,5,10|3,7,8
9,12|4,5,11|3,6,10|1,2,7,8
9,12|4,5,11|1,2,6,10|3,7,8
1,8,12|9,11|2,7,10|3,4,5,6
1,8,12|9,11|3,6,10|2,4,5,7
1,8,12|9,11|4,5,10|2,3,6,7
1,8,12|9,11|2,3,4,10|5,6,7
2,7,12|9,11|1,8,10|3,4,5,6
3,6,12|9,11|1,8,10|2,4,5,7
4,5,12|9,11|1,8,10|2,3,6,7
2,3,4,12|9,11|1,8,10|5,6,7
2,7,12|9,11|3,6,10|1,4,5,8
2,7,12|9,11|4,5,10|1,3,6,8
2,7,12|9,11|1,3,5,10|4,6,8
3,6,12|9,11|2,7,10|1,4,5,8
4,5,12|9,11|2,7,10|1,3,6,8
1,3,5,12|9,11|2,7,10|4,6,8
3,6,12|9,11|4,5,10|1,2,7,8
1,2,6,12|9,11|4,5,10|3,7,8
4,5,12|9,11|3,6,10|1,2,7,8
4,5,12|9,11|1,2,6,10|3,7,8
1,8,12|2,7,11|9,10|3,4,5,6
1,8,12|3,6,11|9,10|2,4,5,7
1,8,12|4,5,11|9,10|2,3,6,7
1,8,12|2,3,4,11|9,10|5,6,7
2,7,12|1,8,11|9,10|3,4,5,6
3,6,12|1,8,11|9,10|2,4,5,7
4,5,12|1,8,11|9,10|2,3,6,7
2,3,4,12|1,8,11|9,10|5,6,7
2,7,12|3,6,11|9,10|1,4,5,8
2,7,12|4,5,11|9,10|1,3,6,8
2,7,12|1,3,5,11|9,10|4,6,8
3,6,12|2,7,11|9,10|1,4,5,8
4,5,12|2,7,11|9,10|1,3,6,8
1,3,5,12|2,7,11|9,10|4,6,8
3,6,12|4,5,11|9,10|1,2,7,8
1,2,6,12|4,5,11|9,10|3,7,8
4,5,12|3,6,11|9,10|1,2,7,8
4,5,12|1,2,6,11|9,10|3,7,8
1,8,12|2,7,11|3,6,10|4,5,9
1,8,12|2,7,11|4,5,10|3,6,9
1,8,12|3,6,11|2,7,10|4,5,9
1,8,12|4,5,11|2,7,10|3,6,9
1,8,12|3,6,11|4,5,10|2,7,9
1,8,12|4,5,11|3,6,10|2,7,9
2,7,12|1,8,11|3,6,10|4,5,9
2,7,12|1,8,11|4,5,10|3,6,9
3,6,12|1,8,11|2,7,10|4,5,9
4,5,12|1,8,11|2,7,10|3,6,9
3,6,12|1,8,11|4,5,10|2,7,9
4,5,12|1,8,11|3,6,10|2,7,9
2,7,12|3,6,11|1,8,10|4,5,9
2,7,12|4,5,11|1,8,10|3,6,9
3,6,12|2,7,11|1,8,10|4,5,9
4,5,12|2,7,11|1,8,10|3,6,9
3,6,12|4,5,11|1,8,10|2,7,9
4,5,12|3,6,11|1,8,10|2,7,9
2,7,12|3,6,11|4,5,10|1,8,9
2,7,12|4,5,11|3,6,10|1,8,9
3,6,12|2,7,11|4,5,10|1,8,9
4,5,12|2,7,11|3,6,10|1,8,9
3,6,12|4,5,11|2,7,10|1,8,9
4,5,12|3,6,11|2,7,10|1,8,9
9,12|1,8,11|2,4,6,7|3,5,10
9,12|1,8,11|3,4,5,7|2,6,10
9,12|2,7,11|5,6,8|1,3,4,10
9,12|2,7,11|1,4,6,8|3,5,10
9,12|3,6,11|4,7,8|1,2,5,10
9,12|1,2,6,11|4,7,8|3,5,10
9,12|4,5,11|1,3,7,8|2,6,10
9,12|1,3,5,11|4,7,8|2,6,10
9,12|3,6,11|2,4,5,8|1,7,10
9,12|4,5,11|2,3,6,8|1,7,10
9,12|2,3,4,11|5,6,8|1,7,10
9,12|2,7,11|1,3,4,5,6|8,10
9,12|3,6,11|1,2,4,5,7|8,10
9,12|1,2,6,11|3,4,5,7|8,10
9,12|4,5,11|1,2,3,6,7|8,10
9,12|1,3,5,11|2,4,6,7|8,10
9,12|2,3,4,11|1,5,6,7|8,10
1,8,12|9,11|2,4,6,7|3,5,10
1,8,12|9,11|3,4,5,7|2,6,10
2,7,12|9,11|5,6,8|1,3,4,10
2,7,12|9,11|1,4,6,8|3,5,10
3,6,12|9,11|4,7,8|1,2,5,10
1,2,6,12|9,11|4,7,8|3,5,10
4,5,12|9,11|1,3,7,8|2,6,10
1,3,5,12|9,11|4,7,8|2,6,10
3,6,12|9,11|2,4,5,8|1,7,10
4,5,12|9,11|2,3,6,8|1,7,10
2,3,4,12|9,11|5,6,8|1,7,10
2,7,12|9,11|1,3,4,5,6|8,10
3,6,12|9,11|1,2,4,5,7|8,10
1,2,6,12|9,11|3,4,5,7|8,10
4,5,12|9,11|1,2,3,6,7|8,10
1,3,5,12|9,11|2,4,6,7|8,10
2,3,4,12|9,11|1,5,6,7|8,10
1,8,12|2,7,11|4,6,9|3,5,10
1,8,12|4,5,11|3,7,9|2,6,10
2,7,12|1,8,11|4,6,9|3,5,10
4,5,12|1,8,11|3,7,9|2,6,10
3,6,12|4,5,11|2,8,9|1,7,10
4,5,12|3,6,11|2,8,9|1,7,10
2,7,12|3,6,11|1,4,5,9|8,10
2,7,12|4,5,11|1,3,6,9|8,10
2,7,12|1,3,5,11|4,6,9|8,10
3,6,12|2,7,11|1,4,5,9|8,10
4,5,12|2,7,11|1,3,6,9|8,10
1,3,5,12|2,7,11|4,6,9|8,10
3,6,12|4,5,11|1,2,7,9|8,10
1,2,6,12|4,5,11|3,7,9|8,10
4,5,12|3,6,11|1,2,7,9|8,10
4,5,12|1,2,6,11|3,7,9|8,10
9,12|2,8,10|1,7,11|3,4,5,6
9,12|2,8,10|3,5,11|1,4,6,7
9,12|2,8,10|1,3,4,11|5,6,7
9,12|3,7,10|8,11|1,2,4,5,6
9,12|1,2,7,10|8,11|3,4,5,6
9,12|4,6,10|8,11|1,2,3,5,7
9,12|1,3,6,10|8,11|2,4,5,7
9,12|1,4,5,10|8,11|2,3,6,7
9,12|2,3,5,10|8,11|1,4,6,7
9,12|1,2,3,4,10|8,11|5,6,7
9,12|3,7,10|2,6,11|1,4,5,8
9,12|3,7,10|1,2,5,11|4,6,8
9,12|1,2,7,10|3,5,11|4,6,8
9,12|4,6,10|1,7,11|2,3,5,8
9,12|2,3,5,10|1,7,11|4,6,8
9,12|4,6,10|3,5,11|1,2,7,8
9,12|4,6,10|1,2,5,11|3,7,8
9,12|1,4,5,10|2,6,11|3,7,8
2,7,12|1,9,10|8,11|3,4,5,6
3,6,12|1,9,10|8,11|2,4,5,7
4,5,12|1,9,10|8,11|2,3,6,7
2,3,4,12|1,9,10|8,11|5,6,7
2,7,12|1,9,10|3,5,11|4,6,8
4,5,12|1,9,10|2,6,11|3,7,8
1,8,12|3,7,10|2,6,11|4,5,9
1,8,12|4,6,10|3,5,11|2,7,9
3,6,12|2,8,10|1,7,11|4,5,9
4,5,12|2,8,10|1,7,11|3,6,9
2,7,12|4,6,10|8,11|1,3,5,9
2,7,12|1,3,6,10|8,11|4,5,9
2,7,12|1,4,5,10|8,11|3,6,9
3,6,12|1,2,7,10|8,11|4,5,9
1,2,6,12|3,7,10|8,11|4,5,9
4,5,12|3,7,10|8,11|1,2,6,9
4,5,12|1,2,7,10|8,11|3,6,9
3,6,12|1,4,5,10|8,11|2,7,9
4,5,12|1,3,6,10|8,11|2,7,9
1,3,5,12|4,6,10|8,11|2,7,9
2,7,12|4,6,10|3,5,11|1,8,9
4,5,12|3,7,10|2,6,11|1,8,9
9,12|5,7,8|2,6,11|1,3,4,10
9,12|1,4,7,8|2,6,11|3,5,10
9,12|5,7,8|1,3,4,11|2,6,10
9,12|1,4,7,8|3,5,11|2,6,10
9,12|2,4,6,8|1,7,11|3,5,10
9,12|3,4,5,8|1,7,11|2,6,10
9,12|2,4,6,8|3,5,11|1,7,10
9,12|3,4,5,8|2,6,11|1,7,10
9,12|2,5,6,7|8,11|1,3,4,10
9,12|3,4,6,7|8,11|1,2,5,10
9,12|1,2,4,6,7|8,11|3,5,10
9,12|1,3,4,5,7|8,11|2,6,10
9,12|2,3,4,5,6|8,11|1,7,10
9,12|2,5,6,7|1,3,4,11|8,10
9,12|3,4,6,7|1,2,5,11|8,10
9,12|1,2,4,6,7|3,5,11|8,10
9,12|1,3,4,5,7|2,6,11|8,10
9,12|2,3,4,5,6|1,7,11|8,10
1,8,12|4,7,9|2,6,11|3,5,10
1,8,12|4,7,9|3,5,11|2,6,10
4,5,12|3,8,9|1,7,11|2,6,10
4,5,12|3,8,9|2,6,11|1,7,10
2,7,12|5,6,9|8,11|1,3,4,10
2,7,12|1,4,6,9|8,11|3,5,10
3,6,12|4,7,9|8,11|1,2,5,10
1,2,6,12|4,7,9|8,11|3,5,10
4,5,12|1,3,7,9|8,11|2,6,10
1,3,5,12|4,7,9|8,11|2,6,10
3,6,12|2,4,5,9|8,11|1,7,10
4,5,12|2,3,6,9|8,11|1,7,10
2,3,4,12|5,6,9|8,11|1,7,10
2,7,12|5,6,9|1,3,4,11|8,10
2,7,12|1,4,6,9|3,5,11|8,10
3,6,12|4,7,9|1,2,5,11|8,10
1,2,6,12|4,7,9|3,5,11|8,10
4,5,12|1,3,7,9|2,6,11|8,10
1,3,5,12|4,7,9|2,6,11|8,10
3,6,12|2,4,5,9|1,7,11|8,10
4,5,12|2,3,6,9|1,7,11|8,10
2,3,4,12|5,6,9|1,7,11|8,10
9,12|2,8,10|1,5,6,7|3,4,11
9,12|2,8,10|3,4,5,7|1,6,11
9,12|2,8,10|1,3,4,5,6|7,11
9,12|3,7,10|5,6,8|1,2,4,11
9,12|1,2,7,10|5,6,8|3,4,11
9,12|3,7,10|1,4,6,8|2,5,11
9,12|3,7,10|2,4,5,8|1,6,11
9,12|4,6,10|1,3,7,8|2,5,11
9,12|1,3,6,10|4,7,8|2,5,11
9,12|2,3,5,10|4,7,8|1,6,11
9,12|4,6,10|1,2,3,5,8|7,11
9,12|1,3,6,10|2,4,5,8|7,11
9,12|1,4,5,10|2,3,6,8|7,11
9,12|2,3,5,10|1,4,6,8|7,11
9,12|1,2,3,4,10|5,6,8|7,11
2,7,12|1,9,10|5,6,8|3,4,11
3,6,12|1,9,10|4,7,8|2,5,11
3,6,12|1,9,10|2,4,5,8|7,11
4,5,12|1,9,10|2,3,6,8|7,11
2,3,4,12|1,9,10|5,6,8|7,11
1,8,12|3,7,10|4,6,9|2,5,11
1,8,12|4,6,10|3,7,9|2,5,11
1,8,12|4,6,10|2,3,5,9|7,11
1,8,12|2,3,5,10|4,6,9|7,11
4,5,12|2,8,10|3,7,9|1,6,11
3,6,12|2,8,10|1,4,5,9|7,11
4,5,12|2,8,10|1,3,6,9|7,11
1,3,5,12|2,8,10|4,6,9|7,11
4,5,12|3,7,10|2,8,9|1,6,11
3,6,12|1,4,5,10|2,8,9|7,11
4,5,12|1,3,6,10|2,8,9|7,11
1,3,5,12|4,6,10|2,8,9|7,11
9,12|5,7,8|3,6,10|1,2,4,11
9,12|5,7,8|1,2,6,10|3,4,11
9,12|1,4,7,8|3,6,10|2,5,11
9,12|5,7,8|2,3,4,10|1,6,11
9,12|2,3,7,8|4,5,10|1,6,11
9,12|1,5,6,8|2,7,10|3,4,11
9,12|3,4,5,8|2,7,10|1,6,11
9,12|1,5,6,8|2,3,4,10|7,11
9,12|2,4,6,8|1,3,5,10|7,11
9,12|1,2,3,6,8|4,5,10|7,11
9,12|3,4,5,8|1,2,6,10|7,11
9,12|1,2,4,5,8|3,6,10|7,11
9,12|2,5,6,7|1,8,10|3,4,11
9,12|3,4,6,7|1,8,10|2,5,11
9,12|2,3,4,5,6|1,8,10|7,11
1,8,12|4,7,9|3,6,10|2,5,11
1,8,12|5,6,9|2,7,10|3,4,11
1,8,12|5,6,9|2,3,4,10|7,11
1,8,12|2,3,6,9|4,5,10|7,11
1,8,12|2,4,5,9|3,6,10|7,11
2,7,12|3,8,9|4,5,10|1,6,11
4,5,12|3,8,9|2,7,10|1,6,11
3,6,12|1,2,8,9|4,5,10|7,11
1,2,6,12|3,8,9|4,5,10|7,11
4,5,12|3,8,9|1,2,6,10|7,11
4,5,12|1,2,8,9|3,6,10|7,11
2,7,12|5,6,9|1,8,10|3,4,11
3,6,12|4,7,9|1,8,10|2,5,11
3,6,12|2,4,5,9|1,8,10|7,11
4,5,12|2,3,6,9|1,8,10|7,11
2,3,4,12|5,6,9|1,8,10|7,11
1,8,12|2,5,6,7|9,10|3,4,11
1,8,12|3,4,6,7|9,10|2,5,11
1,8,12|2,3,4,5,6|9,10|7,11
2,7,12|1,5,6,8|9,10|3,4,11
2,7,12|3,4,5,8|9,10|1,6,11
3,6,12|5,7,8|9,10|1,2,4,11
1,2,6,12|5,7,8|9,10|3,4,11
3,6,12|1,4,7,8|9,10|2,5,11
4,5,12|2,3,7,8|9,10|1,6,11
2,3,4,12|5,7,8|9,10|1,6,11
3,6,12|1,2,4,5,8|9,10|7,11
1,2,6,12|3,4,5,8|9,10|7,11
4,5,12|1,2,3,6,8|9,10|7,11
1,3,5,12|2,4,6,8|9,10|7,11
2,3,4,12|1,5,6,8|9,10|7,11
10,11|8,12|3,7,9|1,2,4,5,6
10,11|8,12|1,2,7,9|3,4,5,6
10,11|8,12|4,6,9|1,2,3,5,7
10,11|8,12|1,3,6,9|2,4,5,7
10,11|8,12|1,4,5,9|2,3,6,7
10,11|8,12|2,3,5,9|1,4,6,7
10,11|8,12|1,2,3,4,9|5,6,7
10,11|1,7,12|2,8,9|3,4,5,6
10,11|3,5,12|2,8,9|1,4,6,7
10,11|1,3,4,12|2,8,9|5,6,7
10,11|1,7,12|4,6,9|2,3,5,8
10,11|1,7,12|2,3,5,9|4,6,8
10,11|2,6,12|3,7,9|1,4,5,8
10,11|3,5,12|1,2,7,9|4,6,8
10,11|1,2,5,12|3,7,9|4,6,8
10,11|2,6,12|1,4,5,9|3,7,8
10,11|3,5,12|4,6,9|1,2,7,8
10,11|1,2,5,12|4,6,9|3,7,8
10,11|8,12|1,5,6,7|2,3,4,9
10,11|8,12|2,4,6,7|1,3,5,9
10,11|8,12|1,2,3,6,7|4,5,9
10,11|8,12|3,4,5,7|1,2,6,9
10,11|8,12|1,2,4,5,7|3,6,9
10,11|8,12|1,3,4,5,6|2,7,9
10,11|1,7,12|5,6,8|2,3,4,9
10,11|1,7,12|2,3,6,8|4,5,9
10,11|1,7,12|2,4,5,8|3,6,9
10,11|2,6,12|4,7,8|1,3,5,9
10,11|2,6,12|1,3,7,8|4,5,9
10,11|3,5,12|4,7,8|1,2,6,9
10,11|1,2,5,12|4,7,8|3,6,9
10,11|3,5,12|1,4,6,8|2,7,9
10,11|1,3,4,12|5,6,8|2,7,9
10,11|2,6,12|3,4,5,7|1,8,9
10,11|3,5,12|2,4,6,7|1,8,9
1,9,11|8,12|2,7,10|3,4,5,6
1,9,11|8,12|3,6,10|2,4,5,7
1,9,11|8,12|4,5,10|2,3,6,7
1,9,11|8,12|2,3,4,10|5,6,7
1,9,11|3,5,12|2,7,10|4,6,8
1,9,11|2,6,12|4,5,10|3,7,8
2,8,11|1,7,12|9,10|3,4,5,6
2,8,11|3,5,12|9,10|1,4,6,7
2,8,11|1,3,4,12|9,10|5,6,7
3,7,11|8,12|9,10|1,2,4,5,6
1,2,7,11|8,12|9,10|3,4,5,6
4,6,11|8,12|9,10|1,2,3,5,7
1,3,6,11|8,12|9,10|2,4,5,7
1,4,5,11|8,12|9,10|2,3,6,7
2,3,5,11|8,12|9,10|1,4,6,7
1,2,3,4,11|8,12|9,10|5,6,7
3,7,11|2,6,12|9,10|1,4,5,8
3,7,11|1,2,5,12|9,10|4,6,8
1,2,7,11|3,5,12|9,10|4,6,8
4,6,11|1,7,12|9,10|2,3,5,8
2,3,5,11|1,7,12|9,10|4,6,8
4,6,11|3,5,12|9,10|1,2,7,8
4,6,11|1,2,5,12|9,10|3,7,8
1,4,5,11|2,6,12|9,10|3,7,8
2,8,11|1,7,12|3,6,10|4,5,9
2,8,11|1,7,12|4,5,10|3,6,9
3,7,11|8,12|1,2,6,10|4,5,9
1,2,7,11|8,12|3,6,10|4,5,9
3,7,11|8,12|4,5,10|1,2,6,9
1,2,7,11|8,12|4,5,10|3,6,9
4,6,11|8,12|2,7,10|1,3,5,9
1,3,6,11|8,12|2,7,10|4,5,9
1,4,5,11|8,12|2,7,10|3,6,9
4,6,11|8,12|1,3,5,10|2,7,9
1,3,6,11|8,12|4,5,10|2,7,9
1,4,5,11|8,12|3,6,10|2,7,9
3,7,11|2,6,12|1,8,10|4,5,9
4,6,11|3,5,12|1,8,10|2,7,9
3,7,11|2,6,12|4,5,10|1,8,9
4,6,11|3,5,12|2,7,10|1,8,9
1,9,11|8,12|2,4,6,7|3,5,10
1,9,11|8,12|3,4,5,7|2,6,10
1,9,11|2,6,12|4,7,8|3,5,10
1,9,11|3,5,12|4,7,8|2,6,10
1,9,11|2,6,12|3,4,5,7|8,10
1,9,11|3,5,12|2,4,6,7|8,10
2,8,11|1,7,12|4,6,9|3,5,10
2,8,11|3,5,12|4,6,9|1,7,10
3,7,11|8,12|4,6,9|1,2,5,10
1,2,7,11|8,12|4,6,9|3,5,10
3,7,11|8,12|1,4,5,9|2,6,10
4,6,11|8,12|3,7,9|1,2,5,10
4,6,11|8,12|1,2,7,9|3,5,10
1,4,5,11|8,12|3,7,9|2,6,10
4,6,11|8,12|2,3,5,9|1,7,10
2,3,5,11|8,12|4,6,9|1,7,10
4,6,11|1,7,12|2,8,9|3,5,10
4,6,11|3,5,12|2,8,9|1,7,10
3,7,11|2,6,12|1,4,5,9|8,10
3,7,11|1,2,5,12|4,6,9|8,10
1,2,7,11|3,5,12|4,6,9|8,10
4,6,11|1,7,12|2,3,5,9|8,10
2,3,5,11|1,7,12|4,6,9|8,10
4,6,11|3,5,12|1,2,7,9|8,10
4,6,11|1,2,5,12|3,7,9|8,10
1,4,5,11|2,6,12|3,7,9|8,10
2,9,10|8,12|1,7,11|3,4,5,6
2,9,10|8,12|3,5,11|1,4,6,7
2,9,10|8,12|1,3,4,11|5,6,7
2,9,10|1,7,12|8,11|3,4,5,6
2,9,10|3,5,12|8,11|1,4,6,7
2,9,10|1,3,4,12|8,11|5,6,7
2,9,10|1,7,12|3,5,11|4,6,8
2,9,10|3,5,12|1,7,11|4,6,8
3,8,10|1,7,12|2,6,11|4,5,9
3,8,10|2,6,12|1,7,11|4,5,9
4,7,10|8,12|2,6,11|1,3,5,9
1,3,7,10|8,12|2,6,11|4,5,9
4,7,10|8,12|3,5,11|1,2,6,9
4,7,10|8,12|1,2,5,11|3,6,9
5,6,10|8,12|1,7,11|2,3,4,9
2,3,6,10|8,12|1,7,11|4,5,9
2,4,5,10|8,12|1,7,11|3,6,9
5,6,10|8,12|1,3,4,11|2,7,9
1,4,6,10|8,12|3,5,11|2,7,9
4,7,10|2,6,12|8,11|1,3,5,9
1,3,7,10|2,6,12|8,11|4,5,9
4,7,10|3,5,12|8,11|1,2,6,9
4,7,10|1,2,5,12|8,11|3,6,9
5,6,10|1,7,12|8,11|2,3,4,9
2,3,6,10|1,7,12|8,11|4,5,9
2,4,5,10|1,7,12|8,11|3,6,9
5,6,10|1,3,4,12|8,11|2,7,9
1,4,6,10|3,5,12|8,11|2,7,9
4,7,10|2,6,12|3,5,11|1,8,9
4,7,10|3,5,12|2,6,11|1,8,9
4,8,9|1,7,12|2,6,11|3,5,10
4,8,9|1,7,12|3,5,11|2,6,10
4,8,9|2,6,12|1,7,11|3,5,10
4,8,9|3,5,12|1,7,11|2,6,10
4,8,9|2,6,12|3,5,11|1,7,10
4,8,9|3,5,12|2,6,11|1,7,10
5,7,9|8,12|2,6,11|1,3,4,10
1,4,7,9|8,12|2,6,11|3,5,10
5,7,9|8,12|1,3,4,11|2,6,10
1,4,7,9|8,12|3,5,11|2,6,10
2,4,6,9|8,12|1,7,11|3,5,10
3,4,5,9|8,12|1,7,11|2,6,10
2,4,6,9|8,12|3,5,11|1,7,10
3,4,5,9|8,12|2,6,11|1,7,10
5,7,9|2,6,12|8,11|1,3,4,10
1,4,7,9|2,6,12|8,11|3,5,10
5,7,9|1,3,4,12|8,11|2,6,10
1,4,7,9|3,5,12|8,11|2,6,10
2,4,6,9|1,7,12|8,11|3,5,10
3,4,5,9|1,7,12|8,11|2,6,10
2,4,6,9|3,5,12|8,11|1,7,10
3,4,5,9|2,6,12|8,11|1,7,10
5,7,9|2,6,12|1,3,4,11|8,10
1,4,7,9|2,6,12|3,5,11|8,10
5,7,9|1,3,4,12|2,6,11|8,10
1,4,7,9|3,5,12|2,6,11|8,10
2,4,6,9|1,7,12|3,5,11|8,10
3,4,5,9|1,7,12|2,6,11|8,10
2,4,6,9|3,5,12|1,7,11|8,10
3,4,5,9|2,6,12|1,7,11|8,10
2,9,10|8,12|1,5,6,7|3,4,11
2,9,10|8,12|3,4,5,7|1,6,11
2,9,10|8,12|1,3,4,5,6|7,11
2,9,10|1,7,12|5,6,8|3,4,11
2,9,10|3,5,12|4,7,8|1,6,11
2,9,10|3,5,12|1,4,6,8|7,11
2,9,10|1,3,4,12|5,6,8|7,11
3,8,10|1,7,12|4,6,9|2,5,11
3,8,10|2,6,12|1,4,5,9|7,11
3,8,10|1,2,5,12|4,6,9|7,11
1,2,8,10|3,5,12|4,6,9|7,11
4,7,10|8,12|1,3,6,9|2,5,11
1,3,7,10|8,12|4,6,9|2,5,11
4,7,10|8,12|2,3,5,9|1,6,11
5,6,10|8,12|3,7,9|1,2,4,11
5,6,10|8,12|1,2,7,9|3,4,11
1,4,6,10|8,12|3,7,9|2,5,11
2,4,5,10|8,12|3,7,9|1,6,11
5,6,10|8,12|1,2,3,4,9|7,11
1,4,6,10|8,12|2,3,5,9|7,11
2,3,6,10|8,12|1,4,5,9|7,11
2,4,5,10|8,12|1,3,6,9|7,11
1,2,3,5,10|8,12|4,6,9|7,11
4,7,10|3,5,12|2,8,9|1,6,11
5,6,10|1,7,12|2,8,9|3,4,11
5,6,10|1,3,4,12|2,8,9|7,11
1,4,6,10|3,5,12|2,8,9|7,11
4,8,9|1,7,12|3,6,10|2,5,11
4,8,9|3,5,12|2,7,10|1,6,11
4,8,9|2,6,12|1,3,5,10|7,11
1,3,8,9|2,6,12|4,5,10|7,11
4,8,9|3,5,12|1,2,6,10|7,11
4,8,9|1,2,5,12|3,6,10|7,11
5,7,9|8,12|3,6,10|1,2,4,11
5,7,9|8,12|1,2,6,10|3,4,11
1,4,7,9|8,12|3,6,10|2,5,11
5,7,9|8,12|2,3,4,10|1,6,11
2,3,7,9|8,12|4,5,10|1,6,11
1,5,6,9|8,12|2,7,10|3,4,11
3,4,5,9|8,12|2,7,10|1,6,11
1,5,6,9|8,12|2,3,4,10|7,11
2,4,6,9|8,12|1,3,5,10|7,11
1,2,3,6,9|8,12|4,5,10|7,11
3,4,5,9|8,12|1,2,6,10|7,11
1,2,4,5,9|8,12|3,6,10|7,11
5,7,9|2,6,12|1,8,10|3,4,11
2,4,6,9|3,5,12|1,8,10|7,11
3,4,5,9|2,6,12|1,8,10|7,11
6,7,8|3,5,12|9,10|1,2,4,11
6,7,8|1,2,5,12|9,10|3,4,11
6,7,8|1,3,4,12|9,10|2,5,11
1,5,7,8|2,6,12|9,10|3,4,11
2,4,7,8|3,5,12|9,10|1,6,11
2,5,6,8|1,7,12|9,10|3,4,11
3,4,6,8|1,7,12|9,10|2,5,11
2,5,6,8|1,3,4,12|9,10|7,11
3,4,6,8|1,2,5,12|9,10|7,11
1,2,4,6,8|3,5,12|9,10|7,11
1,3,4,5,8|2,6,12|9,10|7,11
3,5,6,7|8,12|9,10|1,2,4,11
1,2,5,6,7|8,12|9,10|3,4,11
1,3,4,6,7|8,12|9,10|2,5,11
2,3,4,5,7|8,12|9,10|1,6,11
1,2,3,4,5,6|8,12|9,10|7,11
10,11|3,8,9|7,12|1,2,4,5,6
10,11|1,2,8,9|7,12|3,4,5,6
10,11|3,8,9|1,6,12|2,4,5,7
10,11|3,8,9|2,5,12|1,4,6,7
10,11|3,8,9|1,2,4,12|5,6,7
10,11|1,2,8,9|3,4,12|5,6,7
10,11|4,7,9|1,6,12|2,3,5,8
10,11|4,7,9|2,5,12|1,3,6,8
10,11|1,3,7,9|2,5,12|4,6,8
10,11|5,6,9|7,12|1,2,3,4,8
10,11|1,4,6,9|7,12|2,3,5,8
10,11|2,3,6,9|7,12|1,4,5,8
10,11|2,4,5,9|7,12|1,3,6,8
10,11|1,2,3,5,9|7,12|4,6,8
10,11|5,6,9|3,4,12|1,2,7,8
10,11|5,6,9|1,2,4,12|3,7,8
10,11|1,4,6,9|2,5,12|3,7,8
10,11|2,4,5,9|1,6,12|3,7,8
10,11|5,7,8|1,6,12|2,3,4,9
10,11|2,3,7,8|1,6,12|4,5,9
10,11|5,7,8|3,4,12|1,2,6,9
10,11|5,7,8|1,2,4,12|3,6,9
10,11|1,4,7,8|2,5,12|3,6,9
10,11|1,5,6,8|7,12|2,3,4,9
10,11|2,4,6,8|7,12|1,3,5,9
10,11|1,2,3,6,8|7,12|4,5,9
10,11|3,4,5,8|7,12|1,2,6,9
10,11|1,2,4,5,8|7,12|3,6,9
10,11|1,5,6,8|3,4,12|2,7,9
10,11|3,4,5,8|1,6,12|2,7,9
10,11|2,5,6,7|3,4,12|1,8,9
10,11|3,4,6,7|2,5,12|1,8,9
10,11|2,3,4,5,6|7,12|1,8,9
1,9,11|2,8,10|7,12|3,4,5,6
1,9,11|2,8,10|3,4,12|5,6,7
1,9,11|3,7,10|2,5,12|4,6,8
1,9,11|4,6,10|7,12|2,3,5,8
1,9,11|2,3,5,10|7,12|4,6,8
1,9,11|4,6,10|2,5,12|3,7,8
2,8,11|1,9,10|7,12|3,4,5,6
2,8,11|1,9,10|3,4,12|5,6,7
3,7,11|1,9,10|2,5,12|4,6,8
4,6,11|1,9,10|7,12|2,3,5,8
2,3,5,11|1,9,10|7,12|4,6,8
4,6,11|1,9,10|2,5,12|3,7,8
2,8,11|3,7,10|1,6,12|4,5,9
2,8,11|4,6,10|7,12|1,3,5,9
2,8,11|1,3,6,10|7,12|4,5,9
2,8,11|1,4,5,10|7,12|3,6,9
3,7,11|2,8,10|1,6,12|4,5,9
4,6,11|2,8,10|7,12|1,3,5,9
1,3,6,11|2,8,10|7,12|4,5,9
1,4,5,11|2,8,10|7,12|3,6,9
3,7,11|4,6,10|2,5,12|1,8,9
4,6,11|3,7,10|2,5,12|1,8,9
4,6,11|2,3,5,10|7,12|1,8,9
2,3,5,11|4,6,10|7,12|1,8,9
1,9,11|5,7,8|3,4,12|2,6,10
1,9,11|2,4,6,8|7,12|3,5,10
1,9,11|3,4,5,8|7,12|2,6,10
1,9,11|2,5,6,7|3,4,12|8,10
1,9,11|3,4,6,7|2,5,12|8,10
1,9,11|2,3,4,5,6|7,12|8,10
2,8,11|4,7,9|1,6,12|3,5,10
2,8,11|5,6,9|7,12|1,3,4,10
2,8,11|1,4,6,9|7,12|3,5,10
2,8,11|5,6,9|3,4,12|1,7,10
4,6,11|3,8,9|7,12|1,2,5,10
4,6,11|1,2,8,9|7,12|3,5,10
1,4,5,11|3,8,9|7,12|2,6,10
4,6,11|3,8,9|2,5,12|1,7,10
3,7,11|5,6,9|1,2,4,12|8,10
1,2,7,11|5,6,9|3,4,12|8,10
3,7,11|1,4,6,9|2,5,12|8,10
3,7,11|2,4,5,9|1,6,12|8,10
4,6,11|1,3,7,9|2,5,12|8,10
1,3,6,11|4,7,9|2,5,12|8,10
2,3,5,11|4,7,9|1,6,12|8,10
4,6,11|1,2,3,5,9|7,12|8,10
1,3,6,11|2,4,5,9|7,12|8,10
1,4,5,11|2,3,6,9|7,12|8,10
2,3,5,11|1,4,6,9|7,12|8,10
1,2,3,4,11|5,6,9|7,12|8,10
2,9,10|1,8,11|7,12|3,4,5,6
2,9,10|1,8,11|3,4,12|5,6,7
2,9,10|3,6,11|7,12|1,4,5,8
2,9,10|4,5,11|7,12|1,3,6,8
2,9,10|1,3,5,11|7,12|4,6,8
2,9,10|4,5,11|1,6,12|3,7,8
3,8,10|9,11|7,12|1,2,4,5,6
1,2,8,10|9,11|7,12|3,4,5,6
3,8,10|9,11|1,6,12|2,4,5,7
3,8,10|9,11|2,5,12|1,4,6,7
3,8,10|9,11|1,2,4,12|5,6,7
1,2,8,10|9,11|3,4,12|5,6,7
4,7,10|9,11|1,6,12|2,3,5,8
4,7,10|9,11|2,5,12|1,3,6,8
1,3,7,10|9,11|2,5,12|4,6,8
5,6,10|9,11|7,12|1,2,3,4,8
1,4,6,10|9,11|7,12|2,3,5,8
2,3,6,10|9,11|7,12|1,4,5,8
2,4,5,10|9,11|7,12|1,3,6,8
1,2,3,5,10|9,11|7,12|4,6,8
5,6,10|9,11|3,4,12|1,2,7,8
5,6,10|9,11|1,2,4,12|3,7,8
1,4,6,10|9,11|2,5,12|3,7,8
2,4,5,10|9,11|1,6,12|3,7,8
3,8,10|2,7,11|1,6,12|4,5,9
3,8,10|1,2,6,11|7,12|4,5,9
1,2,8,10|3,6,11|7,12|4,5,9
3,8,10|4,5,11|7,12|1,2,6,9
1,2,8,10|4,5,11|7,12|3,6,9
3,8,10|4,5,11|1,6,12|2,7,9
4,7,10|1,8,11|2,5,12|3,6,9
5,6,10|1,8,11|7,12|2,3,4,9
2,3,6,10|1,8,11|7,12|4,5,9
2,4,5,10|1,8,11|7,12|3,6,9
5,6,10|1,8,11|3,4,12|2,7,9
4,7,10|3,6,11|2,5,12|1,8,9
5,6,10|2,7,11|3,4,12|1,8,9
5,6,10|2,3,4,11|7,12|1,8,9
2,3,6,10|4,5,11|7,12|1,8,9
2,4,5,10|3,6,11|7,12|1,8,9
4,8,9|2,7,11|1,6,12|3,5,10
4,8,9|3,6,11|7,12|1,2,5,10
4,8,9|1,2,6,11|7,12|3,5,10
4,8,9|1,3,5,11|7,12|2,6,10
1,3,8,9|4,5,11|7,12|2,6,10
4,8,9|3,6,11|2,5,12|1,7,10
5,7,9|1,8,11|3,4,12|2,6,10
2,4,6,9|1,8,11|7,12|3,5,10
3,4,5,9|1,8,11|7,12|2,6,10
5,7,9|3,6,11|1,2,4,12|8,10
5,7,9|1,2,6,11|3,4,12|8,10
1,4,7,9|3,6,11|2,5,12|8,10
5,7,9|2,3,4,11|1,6,12|8,10
2,3,7,9|4,5,11|1,6,12|8,10
1,5,6,9|2,7,11|3,4,12|8,10
3,4,5,9|2,7,11|1,6,12|8,10
1,5,6,9|2,3,4,11|7,12|8,10
2,4,6,9|1,3,5,11|7,12|8,10
1,2,3,6,9|4,5,11|7,12|8,10
3,4,5,9|1,2,6,11|7,12|8,10
1,2,4,5,9|3,6,11|7,12|8,10
6,7,8|9,11|2,5,12|1,3,4,10
6,7,8|9,11|3,4,12|1,2,5,10
6,7,8|9,11|1,2,4,12|3,5,10
2,4,7,8|9,11|1,6,12|3,5,10
1,5,7,8|9,11|3,4,12|2,6,10
2,5,6,8|9,11|7,12|1,3,4,10
3,4,6,8|9,11|7,12|1,2,5,10
1,2,4,6,8|9,11|7,12|3,5,10
1,3,4,5,8|9,11|7,12|2,6,10
2,5,6,8|9,11|3,4,12|1,7,10
3,4,6,8|9,11|2,5,12|1,7,10
3,5,6,7|9,11|1,2,4,12|8,10
1,2,5,6,7|9,11|3,4,12|8,10
1,3,4,6,7|9,11|2,5,12|8,10
2,3,4,5,7|9,11|1,6,12|8,10
1,2,3,4,5,6|9,11|7,12|8,10
2,9,10|5,7,8|1,6,12|3,4,11
2,9,10|5,7,8|3,4,12|1,6,11
2,9,10|1,5,6,8|7,12|3,4,11
2,9,10|3,4,5,8|7,12|1,6,11
2,9,10|1,5,6,8|3,4,12|7,11
2,9,10|3,4,5,8|1,6,12|7,11
3,8,10|4,7,9|1,6,12|2,5,11
3,8,10|4,7,9|2,5,12|1,6,11
3,8,10|5,6,9|7,12|1,2,4,11
1,2,8,10|5,6,9|7,12|3,4,11
3,8,10|1,4,6,9|7,12|2,5,11
3,8,10|2,4,5,9|7,12|1,6,11
3,8,10|5,6,9|1,2,4,12|7,11
1,2,8,10|5,6,9|3,4,12|7,11
3,8,10|1,4,6,9|2,5,12|7,11
3,8,10|2,4,5,9|1,6,12|7,11
4,7,10|3,8,9|1,6,12|2,5,11
4,7,10|3,8,9|2,5,12|1,6,11
5,6,10|3,8,9|7,12|1,2,4,11
5,6,10|1,2,8,9|7,12|3,4,11
1,4,6,10|3,8,9|7,12|2,5,11
2,4,5,10|3,8,9|7,12|1,6,11
5,6,10|3,8,9|1,2,4,12|7,11
5,6,10|1,2,8,9|3,4,12|7,11
1,4,6,10|3,8,9|2,5,12|7,11
2,4,5,10|3,8,9|1,6,12|7,11
4,8,9|3,7,10|1,6,12|2,5,11
4,8,9|3,7,10|2,5,12|1,6,11
4,8,9|1,3,6,10|7,12|2,5,11
1,3,8,9|4,6,10|7,12|2,5,11
4,8,9|2,3,5,10|7,12|1,6,11
4,8,9|1,3,6,10|2,5,12|7,11
1,3,8,9|4,6,10|2,5,12|7,11
4,8,9|2,3,5,10|1,6,12|7,11
5,7,9|2,8,10|1,6,12|3,4,11
5,7,9|2,8,10|3,4,12|1,6,11
1,5,6,9|2,8,10|7,12|3,4,11
3,4,5,9|2,8,10|7,12|1,6,11
1,5,6,9|2,8,10|3,4,12|7,11
3,4,5,9|2,8,10|1,6,12|7,11
6,7,8|1,9,10|2,5,12|3,4,11
6,7,8|1,9,10|3,4,12|2,5,11
2,5,6,8|1,9,10|7,12|3,4,11
3,4,6,8|1,9,10|7,12|2,5,11
2,5,6,8|1,9,10|3,4,12|7,11
3,4,6,8|1,9,10|2,5,12|7,11
10,11|3,8,9|1,5,6,7|2,4,12
10,11|3,8,9|2,4,6,7|1,5,12
10,11|3,8,9|1,2,4,5,7|6,12
10,11|1,2,8,9|3,4,5,7|6,12
10,11|4,7,9|5,6,8|1,2,3,12
10,11|1,3,7,9|5,6,8|2,4,12
10,11|4,7,9|2,3,6,8|1,5,12
10,11|4,7,9|1,2,3,5,8|6,12
10,11|1,3,7,9|2,4,5,8|6,12
10,11|5,6,9|4,7,8|1,2,3,12
10,11|5,6,9|1,3,7,8|2,4,12
10,11|2,3,6,9|4,7,8|1,5,12
10,11|2,4,5,9|1,3,7,8|6,12
10,11|1,2,3,5,9|4,7,8|6,12
10,11|5,7,8|4,6,9|1,2,3,12
10,11|5,7,8|1,3,6,9|2,4,12
10,11|2,3,7,8|4,6,9|1,5,12
10,11|5,7,8|1,2,3,4,9|6,12
10,11|1,4,7,8|2,3,5,9|6,12
10,11|2,3,7,8|1,4,5,9|6,12
10,11|1,5,6,8|3,7,9|2,4,12
10,11|2,4,6,8|3,7,9|1,5,12
10,11|3,4,5,8|1,2,7,9|6,12
10,11|1,2,4,5,8|3,7,9|6,12
10,11|3,4,6,7|2,8,9|1,5,12
10,11|1,3,4,5,7|2,8,9|6,12
1,9,11|2,8,10|3,4,5,7|6,12
1,9,11|3,7,10|5,6,8|2,4,12
1,9,11|3,7,10|2,4,5,8|6,12
1,9,11|2,3,5,10|4,7,8|6,12
2,8,11|1,9,10|3,4,5,7|6,12
3,7,11|1,9,10|5,6,8|2,4,12
3,7,11|1,9,10|2,4,5,8|6,12
2,3,5,11|1,9,10|4,7,8|6,12
2,8,11|3,7,10|4,6,9|1,5,12
2,8,11|3,7,10|1,4,5,9|6,12
2,8,11|4,6,10|3,7,9|1,5,12
2,8,11|1,4,5,10|3,7,9|6,12
3,7,11|2,8,10|4,6,9|1,5,12
3,7,11|2,8,10|1,4,5,9|6,12
4,6,11|2,8,10|3,7,9|1,5,12
1,4,5,11|2,8,10|3,7,9|6,12
3,7,11|4,6,10|2,8,9|1,5,12
3,7,11|1,4,5,10|2,8,9|6,12
4,6,11|3,7,10|2,8,9|1,5,12
1,4,5,11|3,7,10|2,8,9|6,12
1,9,11|5,7,8|3,6,10|2,4,12
1,9,11|5,7,8|2,3,4,10|6,12
1,9,11|2,3,7,8|4,5,10|6,12
1,9,11|3,4,5,8|2,7,10|6,12
2,8,11|4,7,9|3,6,10|1,5,12
2,8,11|4,7,9|1,3,5,10|6,12
2,8,11|1,3,7,9|4,5,10|6,12
3,7,11|1,2,8,9|4,5,10|6,12
1,2,7,11|3,8,9|4,5,10|6,12
4,6,11|3,8,9|2,7,10|1,5,12
1,4,5,11|3,8,9|2,7,10|6,12
3,7,11|5,6,9|1,8,10|2,4,12
3,7,11|2,4,5,9|1,8,10|6,12
2,3,5,11|4,7,9|1,8,10|6,12
2,8,11|3,4,6,7|9,10|1,5,12
2,8,11|1,3,4,5,7|9,10|6,12
3,7,11|1,5,6,8|9,10|2,4,12
3,7,11|2,4,6,8|9,10|1,5,12
3,7,11|1,2,4,5,8|9,10|6,12
1,2,7,11|3,4,5,8|9,10|6,12
4,6,11|5,7,8|9,10|1,2,3,12
1,3,6,11|5,7,8|9,10|2,4,12
4,6,11|2,3,7,8|9,10|1,5,12
1,4,5,11|2,3,7,8|9,10|6,12
2,3,5,11|1,4,7,8|9,10|6,12
1,2,3,4,11|5,7,8|9,10|6,12
2,9,10|1,8,11|3,4,5,7|6,12
2,9,10|3,6,11|4,7,8|1,5,12
2,9,10|4,5,11|1,3,7,8|6,12
2,9,10|1,3,5,11|4,7,8|6,12
3,8,10|9,11|1,5,6,7|2,4,12
3,8,10|9,11|2,4,6,7|1,5,12
3,8,10|9,11|1,2,4,5,7|6,12
1,2,8,10|9,11|3,4,5,7|6,12
4,7,10|9,11|5,6,8|1,2,3,12
1,3,7,10|9,11|5,6,8|2,4,12
4,7,10|9,11|2,3,6,8|1,5,12
4,7,10|9,11|1,2,3,5,8|6,12
1,3,7,10|9,11|2,4,5,8|6,12
5,6,10|9,11|4,7,8|1,2,3,12
5,6,10|9,11|1,3,7,8|2,4,12
2,3,6,10|9,11|4,7,8|1,5,12
2,4,5,10|9,11|1,3,7,8|6,12
1,2,3,5,10|9,11|4,7,8|6,12
3,8,10|2,7,11|4,6,9|1,5,12
3,8,10|2,7,11|1,4,5,9|6,12
3,8,10|4,5,11|1,2,7,9|6,12
1,2,8,10|4,5,11|3,7,9|6,12
4,7,10|1,8,11|2,3,5,9|6,12
5,6,10|1,8,11|3,7,9|2,4,12
2,4,5,10|1,8,11|3,7,9|6,12
4,7,10|3,6,11|2,8,9|1,5,12
4,7,10|1,3,5,11|2,8,9|6,12
1,3,7,10|4,5,11|2,8,9|6,12
4,8,9|2,7,11|3,6,10|1,5,12
4,8,9|2,7,11|1,3,5,10|6,12
1,3,8,9|2,7,11|4,5,10|6,12
4,8,9|3,6,11|2,7,10|1,5,12
4,8,9|1,3,5,11|2,7,10|6,12
1,3,8,9|4,5,11|2,7,10|6,12
5,7,9|1,8,11|3,6,10|2,4,12
5,7,9|1,8,11|2,3,4,10|6,12
2,3,7,9|1,8,11|4,5,10|6,12
3,4,5,9|1,8,11|2,7,10|6,12
5,7,9|3,6,11|1,8,10|2,4,12
5,7,9|2,3,4,11|1,8,10|6,12
2,3,7,9|4,5,11|1,8,10|6,12
3,4,5,9|2,7,11|1,8,10|6,12
6,7,8|9,11|4,5,10|1,2,3,12
6,7,8|9,11|1,3,5,10|2,4,12
6,7,8|9,11|2,3,4,10|1,5,12
1,5,7,8|9,11|3,6,10|2,4,12
2,4,7,8|9,11|3,6,10|1,5,12
1,5,7,8|9,11|2,3,4,10|6,12
2,4,7,8|9,11|1,3,5,10|6,12
1,2,3,7,8|9,11|4,5,10|6,12
3,4,6,8|9,11|2,7,10|1,5,12
1,3,4,5,8|9,11|2,7,10|6,12
3,5,6,7|9,11|1,8,10|2,4,12
2,3,4,5,7|9,11|1,8,10|6,12
6,7,8|4,5,11|9,10|1,2,3,12
6,7,8|1,3,5,11|9,10|2,4,12
6,7,8|2,3,4,11|9,10|1,5,12
1,5,7,8|3,6,11|9,10|2,4,12
2,4,7,8|3,6,11|9,10|1,5,12
1,5,7,8|2,3,4,11|9,10|6,12
2,4,7,8|1,3,5,11|9,10|6,12
1,2,3,7,8|4,5,11|9,10|6,12
3,4,6,8|2,7,11|9,10|1,5,12
1,3,4,5,8|2,7,11|9,10|6,12
3,5,6,7|1,8,11|9,10|2,4,12
2,3,4,5,7|1,8,11|9,10|6,12
2,9,10|5,7,8|1,3,4,11|6,12
2,9,10|1,4,7,8|3,5,11|6,12
2,9,10|3,4,5,8|1,7,11|6,12
2,9,10|3,4,6,7|8,11|1,5,12
2,9,10|1,3,4,5,7|8,11|6,12
3,8,10|4,7,9|2,6,11|1,5,12
3,8,10|4,7,9|1,2,5,11|6,12
1,2,8,10|4,7,9|3,5,11|6,12
3,8,10|5,6,9|1,7,11|2,4,12
3,8,10|2,4,5,9|1,7,11|6,12
4,7,10|3,8,9|2,6,11|1,5,12
4,7,10|3,8,9|1,2,5,11|6,12
4,7,10|1,2,8,9|3,5,11|6,12
5,6,10|3,8,9|1,7,11|2,4,12
2,4,5,10|3,8,9|1,7,11|6,12
4,7,10|5,6,9|8,11|1,2,3,12
1,3,7,10|5,6,9|8,11|2,4,12
4,7,10|2,3,6,9|8,11|1,5,12
4,7,10|1,2,3,5,9|8,11|6,12
1,3,7,10|2,4,5,9|8,11|6,12
5,6,10|4,7,9|8,11|1,2,3,12
5,6,10|1,3,7,9|8,11|2,4,12
2,3,6,10|4,7,9|8,11|1,5,12
2,4,5,10|1,3,7,9|8,11|6,12
1,2,3,5,10|4,7,9|8,11|6,12
4,8,9|3,7,10|2,6,11|1,5,12
4,8,9|3,7,10|1,2,5,11|6,12
4,8,9|1,2,7,10|3,5,11|6,12
4,8,9|2,3,5,10|1,7,11|6,12
5,7,9|2,8,10|1,3,4,11|6,12
1,4,7,9|2,8,10|3,5,11|6,12
3,4,5,9|2,8,10|1,7,11|6,12
5,7,9|4,6,10|8,11|1,2,3,12
5,7,9|1,3,6,10|8,11|2,4,12
2,3,7,9|4,6,10|8,11|1,5,12
5,7,9|1,2,3,4,10|8,11|6,12
1,4,7,9|2,3,5,10|8,11|6,12
2,3,7,9|1,4,5,10|8,11|6,12
1,5,6,9|3,7,10|8,11|2,4,12
2,4,6,9|3,7,10|8,11|1,5,12
3,4,5,9|1,2,7,10|8,11|6,12
1,2,4,5,9|3,7,10|8,11|6,12
6,7,8|1,9,10|3,5,11|2,4,12
2,4,7,8|1,9,10|3,5,11|6,12
3,5,6,7|1,9,10|8,11|2,4,12
2,3,4,5,7|1,9,10|8,11|6,12
Zdradź nam
Tomaszu, zdradź nam, do której klasy szkoły podstawowej uczęszczasz.
Tomku!
W zadaniu jest mowa o tarczy zegara. Tak więc zbiory liczb nie mogą łączyć się na zewnątrz tarczy, tak aby rozcięcie tarczy było proste i nie wymagało precyzji chirurga.
Dla przykładu, tworząc zbiór {9, 12} uniemożliwiamy utworzenie zbioru {2, 7, 10} bo wychodziłby on poza tarczę zegara. Jestem przekonany, że wśród uczestników ligi znalazły się dzieci, które poradziły sobie z prawidłowym zrozumieniem tego zadania.
@Krzysztof
Zadanie ma tylko jedno rozwiązanie przy założeniu, że liczby dotykają zewnętrznego okręgu tarczy. Nie wynikało to jednak z treści zadania.
Drogi Tomku
Humaniści to głupi ludzie? Nie! Są mądrzy i nie powinieneś tak pisać. Moja starsza siostra jest humanistką, a mimo to jest wspaniała z matematyki i często wygrywa olimpiady matematyczne. Obrażasz też osobę, która wymyśliła to zadanie. Radzę poćwiczyć umiejętność z I klasy SP, która nazywa się czytanie ze zrozumieniem.