Zad. 1. Pokaż, że co najmniej jedna z liczb dodatnich a, b spełniających warunek (a+b)/2=√(5+ab), jest niewymierna.
Zad. 2. Rozwiąż nierówność x – |7x-3| < 0.
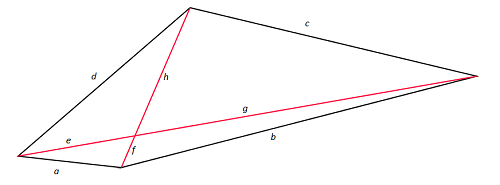
Zad. 3. Czy w dowolnym czworokącie wypukłym suma długości boków przeciwległych jest mniejsza od sumy długości jego przekątnych? Odpowiedź uzasadnij.
W październiku punkty zdobyli:
- 3 - Szymon Bar G 1 Głogówek, Bartłomiej Bychawski GA PWr Wrocław, Dominik Bysiewicz G Dwujęzyczne Krosno, Gracjan Ciupa G 10 Wrocław, Julia Grzyb G Wieliszew, Igor Hołowacz GA PWr Wrocław, Łukasz Janiak GA PWr Wrocław, Alex Kalinowski G Dwujęzyczne Góra, Kosma Kasprzak G 58 Poznań, Marek Komorowski G w ZS 3 Żory, Tomasz Lefler SG Wołów, Jakub Łojko SG Żary, Julia Mazur G Lewin Brzeski, Kacper Misiaczek GA PWr Wrocław, Krzysztof Możdżeń G w ZSO 1 Żory, Krzysztof Nowak GA PWr Wrocław, Magdalena Owczarek G w ZSO Legionowo, Katarzyna Penkalska G Wieliszew, Michał Piórkowski G s. Urszulanek Wrocław, Michał Rzepka G 5 Głogów, Karol Sadowski SG Żary, Kaja Srokosz G 58 Warszawa, Laura Stefanowska G św. Franciszka Legnica, Paulina Szajer GAkademickie PWr Wrocław, Michał Szwej G Dwujęzyczne Chorzów, Łukasz Świszcz GA PWr Wrocław, Julia Waleńdzik G 1 Brzeg Dolny
- 2,5 - Jakub Dobrzański G 3 Lubin, Kacper Gembara SG Wołów, Mateusz Jankowski G 77 Warszawa, Wojciech Rudziński G 1 Głubczyce, Patrycja Zakrzewska G Powiatowe Tuchola
- 2 - Jan Jancewicz GA PWr Wrocław, Weronika Klatka G Imielin, Dawid Konieczko SG Szprotawa, Szymon Kowaliński GA PWr Wrocław, Kacper Kuszaj G 2 Jelcz Laskowice, Krzysztof Mach G 52 Kraków, Mikołaj Mastaliński GA PWr Wrocław,
- 1,5 - Jakub Musiała GA PWr Wrocław, Małgorzata Plewka GA PWr Wrocław, Maciej Płonka GA PWr Wrocław, Jakub Rudzik ???, Mateusz Winiarski G Dwujęzyczne Krosno
- 1 - Julian Wach GA PWr Wrocław
- 0,5 - Konrad Leszczyński GA PWr Wrocław, Marta Zakrzewska G 10 Wrocław.
Pozostali uczestnicy otrzymali poniżej 0,5 punktu.
Zad. 1. Po odpowiednich przekształcenia dostaniemy (a+b)2 = 4(5+ab), a następnie (a–b)2 = 20, skąd |a–b|=2√5. Gdy a>b, mamy a=b+2√5, a gdy b>a, mamy a=b–2√5. Wiedząc, że √5 jest liczbą niewymierną (zatem 2√5 też), łatwo stwierdzić, że przynajmniej jedna z liczb a i b jest niewymierna, ponieważ ani suma, ani różnica dwóch liczb wymiernych a i b nie dałaby w wyniku liczby niewymiernej. Dlaczego?
Zad. 2. Należy rozważyć przypadki gdy x < 3/7 oraz x ≥ 3/7. W pierwszym nierówność przybiera postać x+7x–3<0 ijest spełniona przez liczby x<3/8. W drugim dostajemy nierówność x–7x+3<0, którą spełniają liczby x>1/2. Zatem rozwiązaniem wyjściowej nierówności jest zbiór [tex](-\infty,\frac{3}{8})\cup(\frac{1}{2} , \infty)[/tex]
Zad. 3. Rozważmy dwa przeciwległe boki, np. a i b. Wystarczy skorzystać dwukrotnie z nierówności trójkąta. Wynika z niej, że a < e+f oraz c < g+h. Po dodaniu tych wyrażeń stronami otrzymujemy tezę a+c < e+f+g+h.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
Pytanie do zad. 3.
Czy w zadaniu 3 mowa jest o DOWOLNEJ parze boków przeciwległych czworokąta, czy o co najmniej jednej?
Odp.
Jeśli w zdaniu nie ma kwantyfikatora, oznacza to tzw. duży kwantyfikator "dla każdego". Tylko taki kwantyfikator można opuścić, nie zmieniając sensu zdania. Poza tym odpowiedź na zadanie pytanie wynika natychmiast z rozwiązania.