Zad. 1. Hanka złożyła kwadratową kartkę papieru na pół, otrzymując prostokąt, i jeszcze raz na pół, otrzymując kolejny prostokąt (nie będący kwadratem). Obwód tego drugiego prostokąta wynosił 30 cm. Jakie pole powierzchni miała wyjściowa kartka papieru?
Zad. 2. Rolnik Zenobiusz hoduje kury na jajka i kozy na sery. Właśnie wrócił z giełdy i powiedział do żony: Sprzedałem 80 zwierząt i teraz w naszym gospodarstwie mamy 200 nóg mniej. Ile kóz sprzedał Zenobiusz?
Zad. 3. Zuzanna poszła na wywiadówkę do szkoły syna. W dużej auli ustawiono krzesła w bezpiecznych odległościach: było tam 8 rzędów po 10 krzeseł, a siedziało na nich 54 rodziców. Zuzanna zauważyła, że każdy rodzic albo nie ma żadnego albo ma tylko jednego sąsiada. Jaka jest największa możliwa liczba sąsiednich wolnych krzeseł w jednym rzędzie, jaką mogła zobaczyć Zuzanna?
W listopadzie punkty zdobyli:
- 3 pkt. – Maria Bochenek SP Mieroszów, Ryszard Bogacz SP Smolec, Franciszek Czaplewski SP 11 Inowrocław, Natalia Czurejno SP Wykroty, Mateusz Galik SP Arka Wrocław, Antonina Gembal Prywatna SP Milanówek, Mirosław Gruszczyński SP 9 Gliwice, Maciej Hryniewicz SP 9 Gliwice, Julia Kubeczko SP Studzienice, Wiktor Kuczaj SP 7 Nowa Ruda, Michał Krzyżanowski SP Nasza Szkoła Opole, Aleksander Masztalski SP 3 Mikołów, Joanna Nowakowska SP 3 Głogów, Wiktoria Pietrzak SP Głogów, Maciej Pisowacki SP Mieroszów, Adrian Pokrzywa SP Nowa Wieś, Miłosz Popowicz SP 91 Wrocław, Aleksander Porębny SP 113 Wrocław, Oliwia Raszewska SP 6 Boguszów-Gorce, Oliwia Stańczyk SP Aslan w Głogów, Ignacy Włodarski SP 36 Wrocław, Dominika Wojdacz SP 11 Inowrocław, Anastasiia Yakovleva SP 3 Mogilno;
- 2 pkt. – Jessica Borowczak SP 4 Grodzisk Wlkp, Kevin Charchut SP Iwierzyce, Szymon Czapliński SP 3 Wrocław, Nina Franczak SP Żórawina, Matylda Karpińska SP 187 Warszawa, Mariia Kulyk SP 1 Wrocław, Filip Pawicki SP 64 Wrocław, Bartosz Pawlaczyk SP 107 Wrocław, Wiktor Szwarczyński SP Mieroszów. Kacper Wereszczyński SP Mieroszów, Maciej Wójcik SP 53 Kraków, Dawid Zarębski SP Zachorzów, Tomasz Zawadzki SP Wodzisław;
- 1 pkt. – Aurelia Karpińska SP 187 Warszawa, Wojciech Koliński SP Aslan w Głogów Bartosz Lewandowski SP Żórawina, Mateusz Mika SP Żórawina, Adrianna Orzechowska SP Aslan Głogów, Olaf Orzechowski SP Aslan Głogów, Jan Piątkowski SP 11 Inowrocław, Jan Słomianny SP 29 Wrocław, Dominik Szemberg SP Żórawina, Dorota Turowska SP Białe Błoty, Maria Warachim SP 24 Wocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
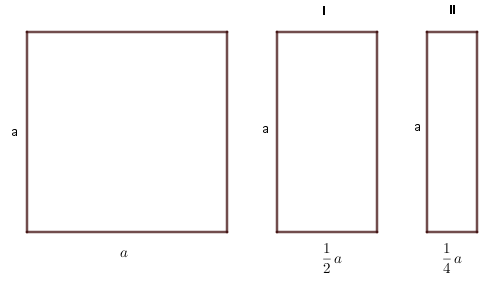
Zad. 1. Niech długość boku kwadratu wynosi a. Wówczas I prostokąt ma boki długości a i a/2, natomiast II prostokąt - długości a i a/4. Obwód drugiego prostokąta wynosi 30 cm, zatem a + a/4=15, skąd a=12, a pole kwadratu wynosi 144 cm2.
Zad. 2. Zenobiusz sprzedał 80 zwierząt. Niech x oznacza liczbę sprzedanych kóz, wówczas 80-x to liczba sprzedanych kur. Ponieważ koza ma cztery nogi a kura dwie, to 4x + 2(80–x) = 200, skąd x=20.
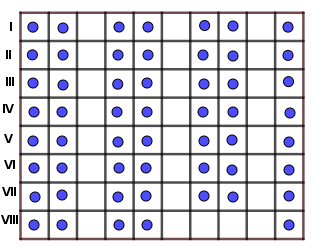
Zad. 3. Aby były spełnione warunki zadania, w jednym rzędzie może usiąść najwyżej 7 osób (rysunek poniżej). Wówczas w ostatnim rzędzie będzie siedziało 54–49 = 5 osób, a największa możliwa liczba sąsiednich wolnych krzeseł wyniesie 4.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
