Zad. 1. W podanym wyrażeniu Marek wpisał w okienko dodatnią liczbę całkowitą, wykonał rachunki i w wyniku otrzymał liczbę naturalną. Jaką liczbę mógł wpisać w okienko? Podaj wszystkie możliwości.
600 : [(32 – 8 · □) : 4]
Zad. 2. Kuba ma 64 jednakowe kostki sześcienne. Pięć ścian każdej z kostek ma kolor biały, a jedna – czerwony. Ze wszystkich posiadanych kostek Kuba zbudował duży sześcian. Ile najwięcej ścianek czerwonych może znaleźć się na wszystkich ścianach tego sześcianu?
Zad. 3. Adam wyjechał z domu rowerem do sklepu oddalonego o 3 km. Jechał ze średnią prędkością 10 km/h. Jego brat Kamil zorientował się, że Adam nie wziął pieniędzy, więc postanowił dogonić go także rowerem. Kamil wyjechał 5 minut później niż Adam i jechał z prędkością 12 km/h. Czy dogoni go na trasie?
W październiku punkty zdobyli:
- 3 pkt. – Klara Bartkowska SP 107 Wrocław, Maria Bochenek SP Mieroszów, Ryszard Bogacz SP Smolec, Jessica Borowczak SP 4 Grodzisk Wlkp, Franciszek Czaplewski SP 11 Inowrocław, Szymon Czapliński SP 3 Wrocław, Natalia Czurejno SP Wykroty, Nina Franczak SP Żórawina, Mateusz Galik SP Arka Wrocław, Mirosław Gruszczyński SP 9 Gliwice, Maciej Hryniewicz SP 9 Gliwice, Wiktor Kuczaj SP 7 Nowa Ruda, Michał Krzyżanowski SP Nasza Szkoła Opole, Mariia, Kulyk SP 1 Wrocław, Aleksander Masztalski SP 3 Mikołów, Joanna Nowakowska SP 3 Głogów, Filip Pawicki SP 64 Wrocław, Maciej Pisowacki SP Mieroszów, Franciszek Płatek SP Żórawina, Miłosz Popowicz SP 91 Wrocław, Aleksander Porębny SP 113 Wrocław, Wiktor Szwarczyński, SP Mieroszów, Maria Warachim SP 24 Wocław, Kacper Wereszczyński SP Mieroszów, Igor Witka SP Żórawina, Ignacy Włodarski SP 36 Wrocław, Dominika Wojdacz SP 11 Inowrocław, Anastasiia Yakovleva SP 3 Mogilno, Dawid Zarębski SP Zachorzów;
- 2,5 pkt. – Filip Domaradzki SP 90 Wrocław, Adrian Kroczak SP Siechnice, Adrian Pokrzywa SP Nowa Wieś, Oliwia Raszewska SP 6 Boguszów-Gorce, Oliwia Stańczyk SP Aslan w Głogów, Tomasz Zawadzki SP Wodzisław;
- 2 pkt. – Przemysław Dykier SP Pruszcz, Antonina Gembal SP Milanówek, Matylda Karpińska SP 187 Warszawa, Aurelia Karpińska SP 187 Warszawa, Mateusz Mika SP Żórawina, Marta Mitlaszewska SP 11 Inowrocław, Bartosz Pawlaczyk SP 107 Wrocław, Jan Słomianny SP 29 Wrocław, Filip Sulski SP 11 Inowrocław, Dorota Turowska SP Białe Błoty, Maciej Wójcik SP 53 Kraków;
- 1,5 pkt. – Jan Piątkowski SP 11 Inowrocław;
- 1 pkt. – Kevin Charchut SP ???, Bartosz Lewandowski SP Żórawina, Adrianna Orzechowska SP Aslan Głogów, Olaf Orzechowski SP Aslan Głogów.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Po wykonaniu dzielenia zawartości okrągłego nawiasu przez 4, podane wyrażenie przyjmuje postać 600 : (8 – 2 · □). Wielkość w nawiasie jest zawsze całkowita (dla naturalnych liczb wpisywanych w okienko), a żeby iloraz był naturalny, wielkość w nawiasie też musi być naturalna, a to zachodzi tylko wtedy, gdy w okienko wstawimy liczby naturalne 1, 2 lub 3. Dla większych liczb zawartość nawiasu jest zerem (i dzielenie jest niewykonalne) lub jest liczba ujemną (i dzielenie daje ujemny wynik). Można sprawdzić, że dla każdej z wymienionych liczb w okrągłym nawiasie otrzymamy naturalny dzielnik liczby 600, więc ostateczny wynik rzeczywiście będzie liczbą naturalną.
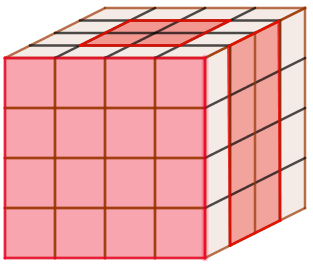
Zad. 2. Sześcian zbudowany przez Kubę przypomina kostkę Rubika o wymiarach 4×4×4 (= 64 sześcianiki).
8 sześcianików w narożnikach pokazuje na zewnątrz swoje 3 ściany, na każdej z 12 krawędzi są jeszcze po 2 sześcianiki, które pokazują swoje 2 ściany, i na każdej z 6 ścian kostki widać jeszcze po 4 sześcianiki, które pokazują na zewnątrz jedną ściankę. Pozostałe 8 sześcianików jest schowanych wewnątrz kostki i nie pokazuje w ogóle swoich ścian. Zatem na powierzchni kostki możemy zobaczyć co najwyżej 8+12·2+6·4 = 56 czerwonych ścianek. Tak sytuację przedstawia np. poniższy rysunek. Czy wiesz, jakie wzory znajdują się na niewidocznych ścianach tego sześcianu?
Zad. 3. Adam Jechał z prędkością 10 km/h, czyli 1 kilometr na 6 minut. Kamil jechał z prędkością 12 km/h czyli 1 kilometr na 5 minut. Na pokonanie trasy o długości 3 km Adam potrzebował 18 minut, a Kamil 15 minut. Ale Kamil wyjechał 5 minut później niż Adam, czyli do sklepu dotarł po 20 minutach od wyjazdu brata z domu, a więc 2 minuty po jego przyjeździe. Zatem nie mógł dogonić go na trasie.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
