Zad. 1. W trójkącie ABC miara kąta ABC wynosi 45°. Dany jest punkt D na odcinku AB taki, że |AD| = 2|DB| oraz |∡ADC| = 60°. Oblicz miarę kąta CAB.
Zad. 2. W trójkącie ABC miary kątów A i B wynoszą po 40°. Niech AL będzie dwusieczną kąta A (L leży na BC). Wykaż, że |AB| = |AL| + |LC|.
Zad. 3. W trójkącie ABC miara kąta C wynosi 81°. CH jest wysokością i |AH| = |HB|+|BC|. Oblicz miarę kąta A.
Zad. 4. (wolna amerykanka) Wewnątrz kwadratu ABCD dany jest punkt P odległy od wierzchołków A, D, C odpowiednio o 1, 2 i 3. Oblicz pole tego kwadratu.
Za zadania 1-3 punkty otrzymali:
- 30 pkt. - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Dominik Bysiewicz (student matematyki na UJ), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Radosław Górzyński (uczeń, I LO Lubin), Sławomir Matysiak (nauczyciel, X LO Wrocław), Mikołaj Popek (student UAM) oraz Tadeusz Porzucek (emerytowany nauczyciel z Gostynia),
- 10 pkt. - Janusz Wieczorek (emerytowany nauczyciel, Sandomierz).
Za zadanie 4 po 10 punktów otrzymali: Jacek Bagiński, Dominik Bysiewicz, Elżbieta Grzechnik, Mikołaj Popek, Tadeusz Porzucek, Janusz Wieczorek oraz Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy).
Gratulujemy!
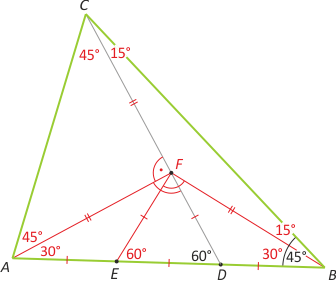
Zad. 1. Niech E będzie środkiem odcinka AD, a F takim punktem na odcinku CD, że |DF| = |DE|. Wówczas trójkąty BDF i EDF są równoramienne, przy czym |∡DFB | = |∡DBF| = 30°, a |∡EFD| = 60°. Stąd kąt EFB jest prosty. Analogicznie trójkąt EFD jest prostokątny, ekierkowy. Z założenia |∡DCB| = 15°, co oznacza, że trójkąt CFB jest równoramienny i mamy |BF| = |CF|. Równoramienny jest także trójkąt ABF, a tym samym trójkąt AFC, przy czym kąt AFC jest prosty. Mamy zatem |∡FCA| = |∡CAF| = 45°. Stąd ostatecznie |∡CAB| = 75°.
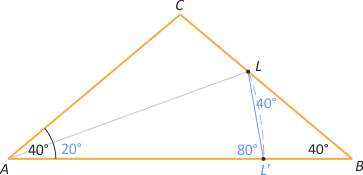
Zad. 2. Niech L' leży na boku AB i zachodzi |AL'| = |AL|. Wówczas w trójkącie równoramiennym AL'L mamy |∡AL'L| = 80°, skąd |∡L'LB| = 40°. Oznacza to, że |LL'| = |L'B|, co ozn. (*). Z drugiej strony z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta mamy |AC|:|AB| = |CL|:|LB|, a z podobieństwa trójkątów ABC i L'BL mamy |AC|:|AB| = |LL'|:|LB|, skąd otrzymujemy |CL|:|LB| = |LL'|:|LB| i dalej |CL| = |LL'|, a wobec (*) mamy tezę.
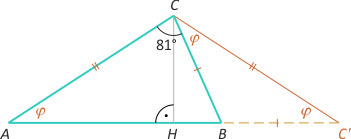
Zad. 3. Przedłużmy bok AB do punktu C' tak, by |BC'| = |BC|. Otrzymujemy wówczas dwa trójkąty równoramienne BC'C oraz AC'C (bo wysokość CH dzieli podstawę AC' na połowy). Oznaczmy miarę kąta A przez φ. Z twierdzenia o sumie kątów wewnętrznych dla trójkąta AC'C otrzymujemy 81° + 3φ = 180°, skąd φ = 33°.
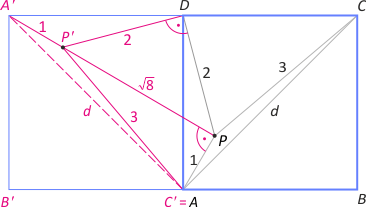
Zad. 4. (wolna amerykanka) Obróćmy kwadrat ABCD o kąt 90° wokół wierzchołka D jak na rysunku. Zauważmy, że trójkąt PDP' jest prostokątny i równoramienny, skąd |P'P| = √8. Z twierdzenia odwrotnego do twierdzenia Pitagorasa wynika, że trójkąt P'AP jest prostokątny, przy czym kąt APP' jest prosty. Z własności obrotu wynika, że odcinek A'P' jest prostopadły do odcinka PA. Oznacza to, że punkty A', P' i P są współliniowe i z twierdzenia Pitagorasa dla trójkąta A'AP mamy |A'A|2 = d2 = |AC|2 = 10 + 2√8. Szukane pole kwadratu wynosi zatem 1/2d2 = 5 + √8.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
