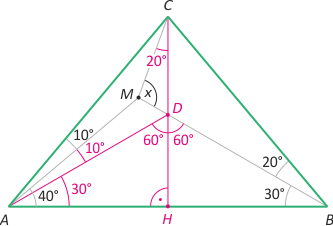
Zad. 1. W trójkącie równoramiennym ABC mamy |AC| = |CB|. Wewnątrz trójkąta obrano punkt M taki, że |∡CAM|=10°, |∡MAB|=40°, |∡ABM|=30° i |∡MBC|=20°. Oblicz |∡BMC|.
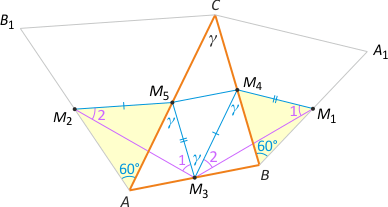
Zad. 2. Na bokach AC i BC trójkąta ABC zbudowano (na zewnątrz ABC) trójkąty równoboczne ACB1 i BCA1. Niech M1, M2 i M3 będą środkami odcinków odpowiednio BA1, AB1 i AB. Znajdź miary kątów trójkąta M1M2M3.
Zad. 3. W trójkącie ABC odcinki AL1 i BL2 są zawarte w dwusiecznych jego kątów wewnętrzych. Niech M i N bedą rzutami prostokątnymi wierzchołka C na te dwusieczne. Wykaż, że odcinek MN jest równoległy do AB i oblicz pole trójkąta MNC, wiedząc że |AB|=10, |AC|=6 i |BC|=8.
Zad. 4. (wolna amerykanka) W trójkącie ABC punkt P leży na odcinku BC, a M – na AC, przy czym |∡APB| = |∡AMB| = 45°. Odcinki AP i BM przecinają się w O. Wiedząc, że pola trójkątów BOP i AOM są równe oraz |BC|=1 i |BO|=√2/2, oblicz pole trójkąta ABC.
Za zadania 1-3 punkty otrzymali:
- 30 - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Dominik Bysiewicz (student matematyki na UJ), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Sławomir Matysiak (nauczyciel, X LO Wrocław), Michał Malik (uczeń, I LO Kraków) i Mikołaj Popek (student UAM),
- 28 - Tadeusz Porzucek (emerytowany nauczyciel z Gostynia),
- 20 - Radosław Górzyński (uczeń, I LO Lubin),
- 18 - Iwona Gruszecka (nauczycielka matematyki, CLV LO Warszawa).
Za zadanie 4 po 10 punktów otrzymali: Jacek Bagiński, Dominik Bysiewicz, Elżbieta Grzechnik, Michał Malik, Mikołaj Popek, Tadeusz Porzucek oraz Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy).
Gratulujemy!
Zad. 1. Niech D będzie takim punktem na wysokości CH, że |∡DAH|=30°. Wówczas |∡ADH|=60° i |∡ADC|=120°. Z drugiej strony |∡MDC=60°|, co oznacza, że MD zawiera się w dwusiecznej kąta ADM. Z kolei AM jest dwusieczną kąta CAD, a stąd CM jest dwusieczną kąta ACD. Zatem |∡MCD|=20° i ostatecznie szukany kąt CMD ma miarę 100°.
Zad. 2. Niech M4 i M5 będą środkami odpowiednio boków BC i AC. Łatwo zauważyć, że trójkąty M2AM5 i M4BM1 są równoboczne (dlaczego?). Dalej |M2M5| = |M3M4| = |AC|/2 oraz |M5M3| = |M4M1| = |BC|/2 jako linie średnie w odpowiednich trójkątach. Zauważmy teraz, że kąty M2M5M3 i M3M4M1 są przystające i mają miarę 60°+γ. Oznacza to, że trójkąty M2M5M3 i M3M4M1 są przystające, zatem |M2M3| = |M3M1| i trójkąt M2M3M1 jest równoramienny, a z sumy kątów w trójkącie M3M4M1 wynika, że |∡M2M3M1| = 120°. Pozostałe szukane kąty mają miarę 30°.
Zad. 3. Przedłużmy CM i CN odpowiednio do CC1 i CC2. Zauważmy, że trójkąty AC2C i C1BC są równoramienne, bo dwusieczne kątów przy wierzchołkach A i B są prostopadłe odpowiednio do podstaw CC2 i CC1. AN i BM są jednocześnie środkowymi, zatem odcinek MN jest linią średnią w trójkącie C1C2C, więc jest równoległy do C1C2, a tym samym do AB. Zauważmy teraz, że |AC1| = 10–8 = 2 oraz |C2B| = 10–6 = 4, a stąd |C1C2|= 4. Wysokość trójkąta CC1C2 jest równa wysokości trójkąta ABC i wynosi 2PABC/|AB| = 2·(1/2·6·8)/10 = 4,8. Pole trójkąta CC1C2 wynosi więc 9,6. Trójkąt CMN jest podobny do trójkąta CC1C2 w skali 1/2, więc PMNC = 2,4.
Zad. 4. (wolna amerykanka) Zauważmy, że pola trójkątów ABM i ABP są równe. Oznacza to, że trójkąty te mają tę samą wysokość opuszczoną na AB, skąd wynika, że odcinek MN jest równoległy do AB, a tym samym czworokąt ABPM jest trapezem. Zauważmy ponadto, że trójkąty AOM i BPO są podobne w skali 1 (bo mają równe pola), czyli są przystające. Trapez i trójkąt ABC są zatem równoramienne. Oznaczmy MO przez x. Wówczas |MC|:|AC| = |MP|:|AB| = |MO|:|OB| = x:(√2/2) = √2x. Mamy |MC| = |AC|·√2x = √2x. Z twierdzenia kosinusów w trójkącie MBC mamy |BC|2 = |MC|2 + |MB|2 – 2|MC|·|MB|·cos135°, a po podstawieniu 1 = 2x2 + (x+√2/2)2 – 2√2x(x+√2/2)·(-√2/2). Po redukcji mamy 10x2 + 4√2x – 1 = 0, skąd x = √2/10 i |MB| = 3√2/5, a |MC| = 1/5. Ostatecznie PABC = 5/4PAMB = 5/4·1/2·|MB|·|MA|·sin45° =
5/4·1/2·(3√2/5)·4/5·(√2/2) = 0,3.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
