luty 2014

Zadanie 1

Fakt. Prawdziwy jest ogólny wzór AH² = 4R²-a², gdzie H oznacza ortocentrum trójkąta ABC (czyli punkt przecięcia prostych zawierających jego wysokości), a jest długością boku BC (leżącego naprzeciw A), a R promieniem okręgu opisanego na trójkącie. Analogicznie BH² = 4R²-b² oraz CH² = 4R²-c².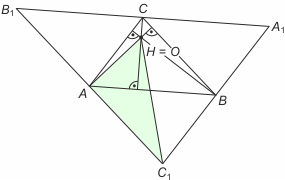
Dowód. Przez wierzchołki trójkąta prowadzimy proste równoległe do boków, otrzymując trójkąt A₁B₁C₁ podobny do wyjściowego w skali k=2. Zauważmy, że wysokości trójkąta ABC zawierają się w symetralnych boków trójkąta A₁B₁C₁. Zatem ortocentrum H jest środkiem okręgu opisanego na A₁B₁C₁. Rozważmy trójkąt AHC₁. Jest on prostokątny (bo AH jest symetralną B₁C₁) oraz AC₁= BC = a (AC₁BC jest równoległobokiem) i HC₁= 2R (ze skali podobieństwa). Z twierdzenia Pitagorasa otrzymujemy podany wzór, a pozostałe - analogicznie.

Przechodząc do rozwiązania zadania, obliczamy pole trójkąta ABC ze wzoru Herona (patrz rozwiązania ze stycznia 2014). Otrzymujemy S = [tex] \sqrt{21 \cdot 8 \cdot 7 \cdot 6}[/tex]= 84. Promień R obliczamy ze wzoru na pole trójkąta S = abc/4R. Otrzymujemy R = 8,125. Stosując udowodniony wyżej wzór, otrzymujemy AH = 8,25.

Fakt. Wzór na pole trójkąta S = abc/4R można uzyskać elementarnie, bez odwoływania się do twierdzenia sinusów.
Dowód. Niech CD będzie średnicą okręgu opisanego na trójkącie ABC. Zauważmy, że trójkąty AH₃C i CDB są podobne z cechy kkk (kąty CAH₃ i CDB są wpisane oparte na tym samym łuku, a kąty AH₃C i CBD są proste). Stąd mamy h_c : b = a : 2R i dalej h_c = ab/2R. Mnożąc obie strony równości przez c/2, otrzymujemy S = ¹/₂·c·h_c = abc/4R.

Zadanie 2

Zauważmy, że kąty KAB i KBA są dopisane do okręgu, oparte na tych samych łukach, co kąty środkowe o miarach 2α i 2β. Stąd ich miary wynoszą odpowiednio α i β. W czworokącie O₁O₂BA z twierdzenia o sumie kątów wynika że 2α+2β = 180°, stąd α+β = 90°. Oznacza to, że kąt AKB jest prosty. Zauważmy teraz, że BT jest średnicą, wiec kąt BKT również jest prosty. Zatem kąt AKT jest półpełny. Stąd wynika teza.

Zadanie 3

Środki okręgów opisanego na trójkącie i weń wpisanego łączy wzór Eulera OI² = R²-2Rr (uzasadnienie poniżej). Podstawiając do niego dane z zadania, otrzymujemy równanie r² = R²-2Rr, a po przekształceniach (R/r)²-2(R/r)-1 = 0, skąd szukany stosunek wynosi R/r = √2+1.

Wzór Eulera. OI² = R²-2Rr
Dowód. Niech trójkąt ABC jest wpisany w okrąg. Niech AW₁ będzie cięciwą okręgu zawartą w dwusiecznej kąta BAC, a W₁D - średnicą okręgu. Niech I oznacza środek okręgu wpisanego w okrąg, a K - jego rzut prostokątny na bok AC. Wówczas trójkąty AIK oraz W₁DB są podobne, bo oba są prostokątne i mają kąt ostry o mierze α/2. Stąd IK : AI = W₁B : W₁D, czyli r : AI = W₁B : 2R. Po przekształceniu otrzymamy AI·W₁B = 2Rr (*).

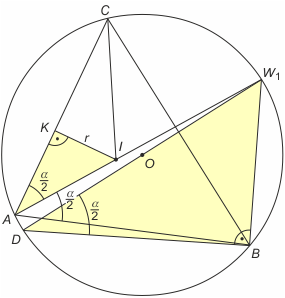
Teraz korzystamy z zasady trójliścia, czyli z faktu, że W₁B = W₁C = W₁I (uzasadnienie poniżej). Podstawiając IW₁ za W₁B do wzoru (*), otrzymujemy AI·IW₁ = 2Rr (**). Teraz przez punkty O i I prowadzimy średnicę MN.

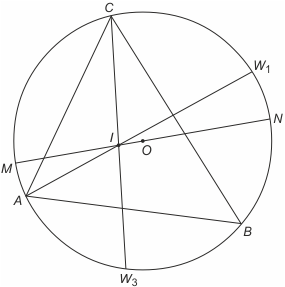
Z twierdzenia o cięciwach okręgu (patrz poniżej) mamy AI·IW₁ = MI·IN = (R-OI)·(R+OI) = R²-OI². Korzystając z (**), otrzymujemy wzór Eulera OI² = R²-2Rr.

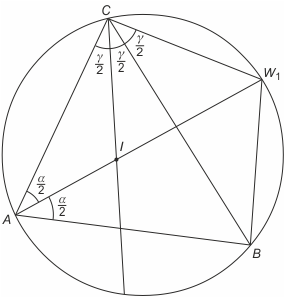
Zasada trójliścia. W₁B = W₁C = W₁I
Dowód. Pierwsza równość jest oczywista, bo AW₁ zawiera się w dwusiecznej kąta BAC. Z drugiej strony zauważmy, że ∡ICW₁ = α/2+γ/2 oraz ∡CIW₁ = α/2+γ/2, bo jest on kątem zewnętrznym trójkąta AIC (a zatem sumą nieprzyległych do niego kątów wewnętrznych tego trójkąta). Oznacza to, że trójkąt IW₁C jest równoramienny przy czym W₁C = W₁I.

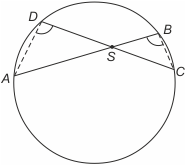Twierdzenie o cięciwach okręgu. Niech AB i CD to cięciwy okręgu przecinające się w punkcie S. Zachodzi AS·BS = CS·DS.
Dowód. Trójkąty ADS i BCS są podobne z cechy kkk (kąty S są wierzchołkowe, kąty D i B - wpisane oparte na tym samym łuku). Zatem zachodzi AS : DS = CS : BS, co po przekształceniu daje tezę.