Od stycznia 2014 zadania Ligi Zadaniowej dla Szkół Ponadgimnazjalnych należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Udowodnij, że wartość poniższej sumy jest liczbą wymierną. [TEX]\sqrt[3]{20+14\sqrt{2}}+\sqrt[3]{20-14\sqrt{2}}[/TEX]
Zad. 2. Pokaż, że jeśli równanie x2+bx+c = 0 ma dwa pierwiastki, to równanie
x2 + (d+1/d) bx + (d+1/d)2 c = 0
również ma dwa pierwiastki dla d≠0.
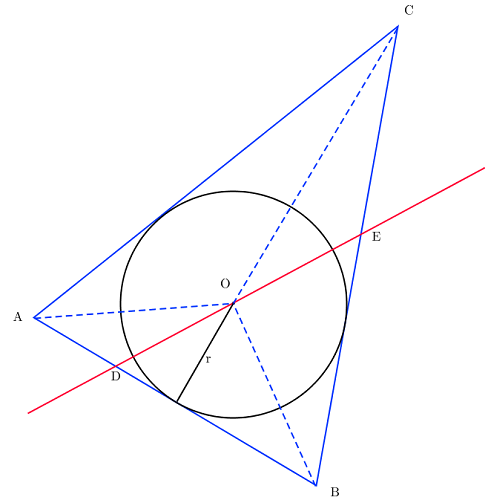
Zad. 3. W trójkąt wpisano okrąg. Pokaż, że dowolna prosta przechodząca przez środek tego okręgu dzieli zarówno obwód jak i pole tego trójkąta w tym samym stosunku.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Kamila Bojar ZSP Szprotawa, Krzysztof Danielak I LO Jelenia Góra, Piotr Dzierza XIII
LO Wrocław, Maciej Golec IX LO Wrocław i Tomasz Stempniak I LO Ostrów Wielkopolski, - 2,5 pkt. - Robert Czwartosz LO Trzebnica,
- 2 pkt. - Krzysztof Bednarek III LO Wrocław.
Pozostali uczestnicy zdobyli poniżej 0,5 punktu.
Po pięciu miesiącach Ligi z wynikiem 14,5 pkt. (na 15 możliwych!) prowadzą Robert Czwartosz z LO w Trzebnicy i Tomasz Stempniak z I LO w Ostrowie Wielkopolskim. Gratulujemy!
Zad. 1.
I sposób (efekciarski): Liczbę 20+14√2 można przedstawić, jako 8+12+12√2+2√2 i dalej, korzystając ze wzoru skróconego mnożenia x3+3x2y+3xy2+y3 = (x+y)3, jako (2+√2)3. Analogicznie liczbę 20-14√2 można przedstawić jako (2-√2)3. Zatem wyjściowa suma wynosi $$\sqrt[3]{20+14\sqrt{2}}+\sqrt[3]{20-14\sqrt{2}}=\sqrt[3]{(2+\sqrt{2})^3}+\sqrt[3]{(2-\sqrt{2})^3}=(2+√2) + (2-√2) = 4 ,$$ czyli jest wymierna.
II sposób (po bożemu): Oznaczmy daną sumę przez x i obliczmy, ile wynosi x3, korzystając z tego samego wzoru skróconego mnożenia, co wyżej. Otrzymamy:
[tex]20+14\sqrt{2}+3\sqrt[3]{(20+14\sqrt{2})^2(20-14\sqrt{2})}+[/tex]
[tex]3\sqrt[3]{(20+14\sqrt{2})(20-14\sqrt{2})^2}+20-14\sqrt{2}[/tex].
Stopniowo upraszczamy powyższe wyrażenie:
[tex]40+3\sqrt[3]{(20+14\sqrt{2})\left(20^2-(14\sqrt{2})^2\right)}+[/tex]
[tex]3\sqrt[3]{(20-14\sqrt{2})\left(20^2-(14\sqrt{2})^2\right)}=[/tex]
[tex]40+3\sqrt[3]{8(20+14\sqrt{2})}+3\sqrt[3]{8(20-14\sqrt{2})}=[/tex]
[tex]40+6\sqrt[3]{20+14\sqrt{2}}+6\sqrt[3]{20-14\sqrt{2}}[/tex].
Tym sposobem otrzymaliśmy równanie x3 = 40+6x lub równoważnie x3-6x-40 = 0. Teraz lewą stronę rozkładamy na czynniki (x-4)(x2+4x+10) = 0. Ponieważ czynnik x2+4x+10 = 0 nigdy nie jest zerem, zerem musi być drugi czynnik, czyli x=4. Pokazaliśmy więc, że dana suma x jest wymierna.
Zad. 2. Skoro równanie x2+bx+c = 0 ma dwa różne pierwiastki, to jego wyróżnik Δ1=b2-4c>0. Z kolei wyróżnik równania x2 + (d+1/d)bx + (d+1/d)2c = 0 jest równy Δ2 = (d+1/d)2b2 - 4(d+1/d)2c = (d+1/d)2(b2-4c) = (d+1/d)2·Δ1, co jest większe od zera, ponieważ (d+1/d)2 > 0.
Zad. 3. Stosunek pola trójkąta BDE do pola czworokąta ACED jest równy$$\frac{P_{BDE}}{P_{ACED}}=\frac{P_{BOD}+P_{BOE}}{P_{AOD}+P_{AOC}+P_{COE}}=\frac{0,5|BD|r+0,5|BE|r}{0,5|AD|r+0,5|AC|r+0,5|CE|r}=\frac{|BD|+|BE|}{|AD|+|AC|+|CE|}\ .$$W przypadku gdy prosta przechodzi przez jeden z wierzchołków trójkąta ABC, rozumowanie upraszcza się, bo porównujemy pola dwóch trójkątów.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
