Uwaga! Rozpoczynając od stycznia 2014, zadania Ligi Zadaniowej dla szkół ponadgimnazjalnych należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Na zegarze ściennym jest godzina 3. Po jakim czasie wskazówka minutowa pokryje się z godzinową, jeśli wskazówki tego zegara poruszają się ruchem ciągłym?
Zad. 2. Uprość wyrażenie: $$\frac{x^2+\frac{1}{x}}{x+\frac{1}{x}-1} . $$
Zad. 3. Wykaż, że połowa sumy długości dwóch boków trójkąta jest większa od długości środkowej opuszczonej na trzeci bok.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Robert Czwartosz LO Trzebnica, Krzysztof Danielak I LO Jelenia Góra, Piotr Dzierza XIII LO Wrocław, Maciej Golec IX LO Wrocław, Marcin Korona XIV LO Warszawa i Tomasz Stempniak I LO Ostrów Wielkopolski,
- 2,5 pkt. - Krzysztof Bednarek III LO Wrocław i Antoni Kamiński III LO Wrocław,
- 2 pkt. - Kamila Bojar ZSP Szprotawa,
- 0,5 pkt. - Przemysław Orman LO Szprotawa.
Pozostali uczestnicy zdobyli poniżej 0,5 punktu. Liga dopiero dobiega do półmetka,
więc w ostatecznej klasyfikacji wszystko jest jeszcze możliwe.
Po czterech miesiącach Ligi z wynikiem 12 pkt. (na 12 możliwych) prowadzi Robert Czwartosz z LO w Trzebnicy. Gratulujemy!
Zad. 1. Wskazówki spotkają się oczywiście pomiędzy 3:15 a 3:20. Niech nastąpi to x minut po godzinie 3:15. W tym czasie wskazówka godzinowa zakreśli na tarczy x minut, a minutowa 15+x minut. Ponieważ wskazówka godzinowa porusza się 12 razy wolniej niż minutowa, w tym samym czasie zakreśla 12 razy krótszą drogę, zatem x = 1/12·(15+x). Stąd x = 15/11 = 14/11. Wskazówki spotkają się 14/11 minuty po godzinie 3:15, czyli po 164/11 minuty po godzinie 3 (to jest około 3:16:22).
Zad. 2. Mnożymy licznik i mianownik ułamka przez x (bo musi być x≠0) i otrzymujemy: $$\frac{x^2+\frac{1}{x}}{x+\frac{1}{x}-1}=\frac{x^3+1}{x^2+1-x}=\frac{(x+1)(x^2-x+1)}{x^2-x+1} .$$ Ponieważ wyrażenie w mianowniku jest stale dodatnie, po skróceniu przez nie otrzymujemy równoważną postać x+1 (dla x≠0).
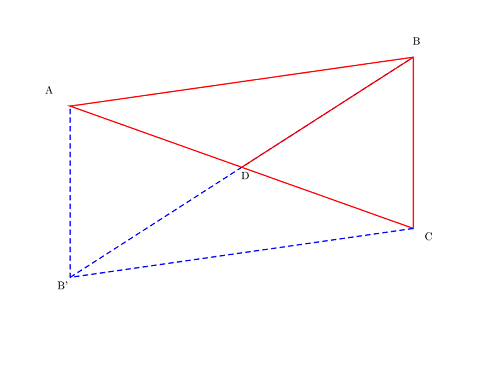
Zad. 3. Dopełniamy trójkąt ABC do równoległoboku ABCB', tak że środkowa BD jest połową przekątnej BB'. Z nierówności trójkąta dla trójkąta BB'C mamy |B'C|+|BC|>|BB'|, czyli |AB|+|BC|>2|BD|. Dzieląc obie strony tej nierówności przez 2, otrzymujemy szukaną tezę.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
