Tekst został napisany w oparciu o arkusz kalkulacyjny MS Excel 2013. Inne wersje Excela mogą się nieznacznie różnić od prezentowanej.
Słoń afrykański to największe zwierzę lądowe. Czy zastanawialiście się kiedyś, ile waży dorosły samiec słonia? A gdybyście oglądali film przyrodniczy, w którym padłaby informacja, że słoń, który jest jego bohaterem, waży 5600 kg, uznalibyście, że jest duży jak na słonia, czy wręcz przeciwnie? A roczne słoniątko ważące 2300 kg?
Sądzę, że mamy-słonice nie zastanawiają się nad tym, czy ich młode są duże czy małe jak na swój wiek, ale nasze mamy na pewno stawiały sobie to pytanie. Szczególnie często takie pytanie pada w najmłodszym wieku, bo to, ile ważymy i ile mierzymy, może świadczyć o naszym harmonijnym rozwoju bądź o tym, że rozwijamy się nieprawidłowo.
A zatem... Czy pięcioletni chłopiec ważący 15 kg jest dobrze zbudowany jak na swój wiek? Może mieści się w normie? A może ma niedowagę? Nie sposób dokonać oceny tego faktu bez porównania masy chłopca z masą wielu jego rówieśników. Jeśli okaże się, że, dajmy na to, bardzo mało jego rówieśników ma mniejszą masę niż on, to możemy wysunąć przypuszczenie, że chłopiec waży za mało. Z kolei gdyby się okazało, że bardzo mało jego rówieśników ma większą masę niż on, mogłoby to sugerować, że chłopiec waży za dużo. W przeciwnym wypadku uznamy, że chłopiec mieści się w normie.
Wzrost czy masa to nie jedyne wielkości, w wypadku których chcielibyśmy wiedzieć, jak jedna osoba prezentuje się na tle większej zbiorowości. Weźmy choćby szkolne oceny lub też wyniki egzaminów na koniec szkoły. Obiektywnie można powiedzieć, że uzyskanie 70% punktów z egzaminu to dobry wynik, ale jeśli stosunkowo mało uczniów osiągnęło lepszy wynik, to można wnioskować, że egzamin zapewne był trudny i być może owe 70% punktów zasługuje na miano wyniku bardzo dobrego.
Podobnie rzecz się ma, jeśli chodzi o dochody. Obecnie średnia miesięczna płaca brutto w Polsce wynosi nieco ponad 4000 zł. Czy automatycznie oznacza to, że ktoś, kto zarabia 3000 zł brutto miesięcznie, zarabia mało? Aby się tego dowiedzieć, trzeba ustalić, jaka część wszystkich zarabiających w Polsce zarabia mniej niż 3000 zł. Dopiero na tej podstawie możemy stwierdzić, czy 3000 zł brutto to mało. A może całkiem sporo.
Nawet gdybyśmy mieli dane odnośnie wszystkich osób pobierających wynagrodzenie w Polsce, trudno by było sporządzić tabelę, w której byłaby informacja, jaka część spośród nich zarabia mniej od każdej kwoty, jaka mogłaby nas interesować. Z drugiej strony taka informacja nie jest na ogół potrzebna. Zamiast tego moglibyśmy sporządzić tabelę, w której byłaby informacja np. o kwocie, od której jedna czwarta dochodów jest mniejsza (i zarazem trzy czwarte większe), kwocie, od której połowa dochodów jest mniejsza i połowa większa, oraz o kwocie, od której trzy czwarte dochodów jest mniejsze (i jedna czwarta większa). Takie trzy liczby dawałyby już jakieś wyobrażenie o dochodach i pozwoliły się zorientować, czy kwota zaproponowana przez kandydata do pracy jako satysfakcjonująca dla niego jest duża czy mała.
Trzy liczby wspomniane powyżej nazywamy kwartylami: odpowiednio pierwszym, drugim i trzecim. Drugi kwartyl nosi też nazwę mediany i nazwa ta jest stosowana częściej niż nazwa drugi kwartyl.
W wypadku oceny postępów w nauce często obliczamy kolejno takie wyniki egzaminu, że odpowiednio 4, 11, 23, 40, 60, 77, 89, 96 procent uzyskanych wyników było od nich mniejsze (a właściwie mniejsze bądź równe). Liczby te dzielą wszystkie wyniki na dziewięć przedziałów zwanych staninami (od angielskiego standard nine). Jeśli chcemy ocenić wynik konkretnego ucznia, możemy powiedzieć, w którym staninie się znalazł.
Liczby, które należało tu wyliczyć, nazywamy odpowiednio czwartym, jedenastym itd. centylem. Zamiennie z nazwą centyl funkcjonuje też nazwa percentyl.
Z kolei do oceny wzrostu i wagi dzieci wybiera się różne centyle, ale często są to: 3., 10., 25., 50., 75., 90. i 97. centyl (czyli kwartyle - to trzy środkowe wartości - i jeszcze cztery inne wartości). Jak łatwo widać, pierwszy kwartyl to inaczej 25. centyl, mediana (drugi kwartyl) to 50. centyl, natomiast trzeci kwartyl to 75. centyl.
W Excelu do obliczenia kwartyli służy funkcja KWARTYL. Jako jej pierwszy argument podajemy zakres danych, w oparciu o które kwartyle mają zostać wyznaczone. Z kolei jako drugi argument możemy podać jedną z liczb: 0, 1, 2, 3, 4. 1, 2 i 3 pozwalają obliczyć odpowiednio pierwszy, drugi (medianę) i trzeci kwartyl. Dodatkowo 0 i 4 pozwalają obliczyć minimum i maksimum z danych.
Z kolei do obliczania centyli używamy funkcji PERCENTYL, która działa podobnie jak funkcja KWARTYL, z tym że jej drugim argumentem jest liczba z zakresu od 0 do 1. A zatem aby obliczyć np. 3 centyl, w funkcji PERCENTYL trzeba podać liczbę 0,03.
Jak to wygląda w praktyce?
Wszystkie obliczenia omówione poniżej znajdują się w tym pliku.
Przykład 1. W arkuszu 1 znajdują się dane o zarobkach w pewnej firmie zatrudniającej ponad 2000 pracowników. Kwartyle zarobków wynoszą w tym wypadku: pierwszy – 2855,23 zł, drugi – 3283,38 zł i trzeci – 3864,62 zł.
Można zatem powiedzieć, że kandydat ubiegający się o zatrudnienie w tej firmie, który oczekuje wynagrodzenia na poziomie 4000 zł, jest dość wymagający, ponieważ kwota ta przekracza trzeci kwartyl zarobków, a więc mniej niż jedna czwarta pracowników tej firmy zarabiałaby więcej niż on.
Uwaga. Przy obliczeniach w arkuszu kalkulacyjnym zastosowaliśmy adresowanie bezwzględne (ze znakami dolara) i przeciąganie formuł. Są to umiejętności z zakresu obsługi arkusza kalkulacyjnego, których nie będziemy tu omawiać.
Przykład 2. W arkuszu 2 znajdują się dane dotyczące wyników z matury z języka polskiego na poziomie podstawowym zdawanej w czerwcu 2015 roku przez uczniów z pewnego powiatu. Odpowiednie centyle służące do wyznaczenia staninów wynoszą kolejo: 33, 36, 39, 43, 47, 50, 54 i 57 punktów.
Wobec tego staniny wynoszą:
pierwszy - poniżej 33 punktów,
drugi - między 33 i 36 punktów,
trzeci - między 36 i 39 punktów,
czwarty - między 39 i 43 punktów,
piąty - między 43 i 47 punktów,
szósty - między 47 i 50 punktów,
siódmy - między 50 i 54 punktów,
ósmy - między 54 i 57 punktów,
dziewiąty - powyżej 57 punktów.
Jeśli jakiś uczeń w tym powiecie uzyskał wynik z matury z matematyki równy 44%, to możemy powiedzieć, że znalazł się on w piątym staninie wyników z matury z języka polskiego w tym powiecie... a więc był to wynik przeciętny w stali tego powiatu.
Przykład 3. W arkuszu 3 znajdują się dane o wzroście pewnej grupy trzynastolatków (płci męskiej), uczniów klas pierwszych pewnego gimnazjum. Wyznaczone na ich podstawie centyle wynoszą:
Możemy zatem powiedzieć, że jeśli chłopiec w tym wieku ma 167 cm, to jest raczej wysoki, ponieważ jego wzrost jest większy niż 90. centyl, a to oznacza, że mniej niż 10% chłopców w tym wieku jest wyższych niż on.
W celu monitorowania wzrostu i wagi dzieci wykonuje się wykresy, które nazywamy siatkami centylowymi. Taką przykładową siatkę centylową dla wzrostu dziewcząt widzimy poniżej:
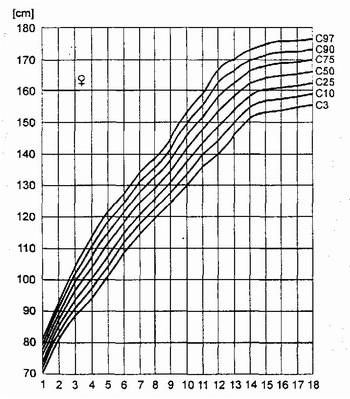
Na osi X zaznaczone są kolejne lata życia (najczęściej od 1 do 18), natomiast na osi Y mamy wzrost w centymetrach. Linie biegnące w poprzek wykresu oznaczają odpowiednie centyle. Widzimy np. że 25. centyl (pierwszy kwartyl) wzrostu 10-latkek wynosi 128 cm. Naturalnie trudno byłoby wyznaczyć centyle dla każdego możliwego wieku (z dokładnością do miesięcy czy dni), więc robi się to dla wieku dziecka z dokładnością do roku, a punkty na wykresie łączy się linią dla nadania wykresowi większej przejrzystości.
Jak zrobić taką siatkę centylową samodzielnie, jeśli dysponowalibyśmy danymi o wzroście odpowiednio dużej liczby dzieci w każdym wieku, który chcielibyśmy rozważać?
Najwygodniej będzie umieścić dane o wzroście poszczególnych roczników w kolejnych kolumnach. Należy zwrócić uwagę, że nie jest konieczne, aby dzieci w każdym wieku było tyle samo. Następnie pod każdą kolumną obliczamy odpowiednie centyle. Wygodnie będzie, jeśli powyżej obliczonych centyli umieścimy wiersz z liczbą lat, której te centyle odpowiadają, a po lewej stronie umieścimy podpisy centyli. Tabela z obliczonymi centylami może wyglądać np. tak:
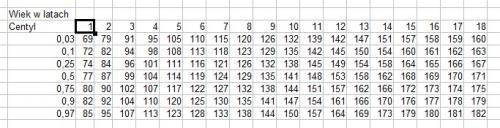
Potem rysujemy wykres dla 3. centyla. W tym celu z dostępnych w Excelu wykresów ze względu na największą przejrzystość wybieramy wykres punktowy z prostymi liniami (ostatni typ spośród wykresów punktowych), a jako dane zaznaczamy wiersz z liczbą lat i wiersz z 3. centylem (wraz z pierwszymi komórkami zawierającymi etykiety "Centyl" i "0,03"). Kolejny centyl rysujemy, klikając na wykres prawym przyciskiem myszy a następnie wybierając opcję "Zaznacz dane". W oknie, które się otworzy, klikamy "Dodaj", po czym jako nazwę serii podajemy komórkę z etykietą 0,1, jako wartości X serii komórki z liczbą lat, a jako wartości Y serii komórki z dziesiątym centylem. Tak samo postępujemy z kolejnymi centylami.
Jeśli wszystko zostało wykonane tak, jak to opisano powyżej, powinniśmy otrzymać wykres wraz z legendą informującą o tym, który kolor na wykresie odpowiada któremu centylowi.
Kwartyle wiążą się z częściami danych o liczbie elementów w stosunku do liczby wszystkich elementów zbioru wyrażonych ułamkami o mianowniku 4. Centyle odnoszą się do ułamków o mianowniku 100. Rozważa się jeszcze decyle (ułamki o mianowniku 10), tercyle (ułamki o mianowniku 3), pentyle (ułamki o mianowniku 5) itd. Jeśli poszukujemy liczby dzielącej zbiór danych w dowolnym stosunku, to mówimy wówczas o kwantylach. Wobec tego można powiedzieć, że tercyle, kwartyle, pentyle, decyle czy centyle to ogólnie kwantyle.
Jeśli ktoś chce poznać ścisły matematyczny opis tego, czym są kwartyle, może zajrzeć do jednego z archiwalnych odcinków ligi.
Z kolei o staninach pisaliśmy już na Wrocławskim Portalu Matematycznym.
Zad. 1. (0,5 punktu) Korzystając z danych dotyczących rodzin pozostających pod opieką pewnej fundacji, jakie posłużyły w jednym z poprzednich odcinków ligi, oblicz pierwszy, drugi i trzeci kwartyl średniego dochodu na osobę w tych rodzinach (kolumna "Dochód").
Zad. 2. (1 punkt) Korzystając z danych dotyczących kandydatów na studia, jakie posłużyły w poprzednich odcinkach ligi, oblicz centyle służące do wyznaczenia staninów wyników z matury TYLKO na poziomie rozszerzonym z matematyki tzn. oblicz centyle na podstawie danych zawartych w kolumnie "Matematyka", ale tylko w tych wierszach, gdzie w kolumnie "Matematyka R" wpisano wartość T. W tym celu przed przystąpieniem do rachunków najlepiej będzie odfiltrować tylko osoby, które zdawały maturę z matematyki na poziomie rozszerzonym. Aby to zrobić, należy kliknąć prawym przyciskiem myszy w dowolnym miejscu tabeli z danymi, z menu kontekstowego wybrać "Filtruj", a następnie rozwinąć pole z nagłówkiem "Matematyka R" i odznaczyć wartość N. Po tym zabiegu całą pozostałą tabelę lub tylko kolumnę z wynikiem maturalnym z matematyki (kolumna "Matematyka") należy skopiować w wkleić w innym miejscu: pod spodem pierwotnej tabeli z danymi lub w innym arkuszu. Warto zdawać sobie sprawę z tego, że wklejanie czegoś obok przefiltrowanej tabeli może być ryzykowne, bo filtrowanie nie usuwa wierszy, a jedynie je ukrywa.
Zad. 3. (1,5 punktu) Na podstawie danych zawartych w arkuszu 4 tego pliku sporządź siatkę centylową zgodnie z opisem zawartym w tekście.
Jako rozwiązanie prześlij utworzony przez siebie plik, w którym do kolejnych arkuszy skopiujesz dane potrzebne do rozwiązania poszczególnych zadań. Arkuszom w pliku nadaj nazwy w taki sposób, by było wiadomo, gdzie znajduje się rozwiązanie danego zadania.
