Zad. 1. Ile co najmniej kilometrów wystarczy przejechać z Wrocławia, aby dotrzeć do:
a) Paryża?
b) Węgier?
c) Ameryki?
Zad. 2. W starym kalkulatorze prostym, który rozpoznaje kolejność działań, funkcjonują tylko klawisze 7, *, = oraz –. Jaką sekwencję klawiszy należy nacisnąć, aby na wyświetlaczu otrzymać wynik jak najbliższy 245?
Zad. 3. Na ile sposobów z poniższego diagramu można odczytać napis WALENTYNKI♥?
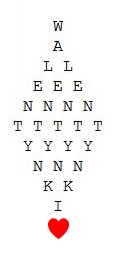
Po łatwym zestawie styczniowym w lutym uczestnikom Ligi trudności sprawiły zadania 1 i 3. Punkty zdobyli:
- 3 pkt. - Andrzej Piasecki - administrator IT z Oleśnicy,
- 2,5 pkt. - Krystyna Lisiowska - redaktor z Warszawy,
- 2 pkt. - Krzysztof Danielak - student Automatyki i Robotyki na PWr,
- 1,5 pkt. - Tomasz Tomiczek - nauczyciel z Lipowej.
Na półmetku Ligi czołówka przedstawia się nastęująco:
- 14,75 pkt. - Andrzej Piasecki
- 12,75 pkt. - Krystyna Lisiowska
- 10,25 pkt. - Tomasz Tomiczek
- 6 pkt. - Krzysztof Danielak
- 3 pkt. - Michał Żłobicki
Zad. 1. W oparciu o bazę GUS'u i Google Maps poprawne odpowiedzi to:
a) 73,4 km do Paryża w gminie Pokój (Domaradz),
b) 21,4 km do Węgier w gminie Żurawina,
c) 77,3 km do Ameryki w gminie Dobrzeń Wielki.
Zad. 2. W zadaniu można uzyskać dokładny wynik, wpisując działanie: 7*7*7–7*7–7*7.
Zad. 3. Tresć zadania nie jest jednoznaczna. Możliwe są dwa podejścia do jego rozwiązania.
1) Jeśli potraktujemy zadanie kombinatorycznie, wybierając z diagramu w dowolny sposób litery tworzące żądany napis, to otrzymamy 1·1·2·3·4·5·4·3·2·1·1 = 2880 sposobów.
2) Jeśli chcemy wyznaczć liczbę możliwych ściezek na diagramie od W do ♥, które dadzą żądany napis, to otrzymamy 70 sposobów. Dlaczego? Zastąpmy każdą literę w diagramie liczbą ścieżek, które do niej prowadzą. Otrzymamy:
1
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
5 10 10 5
15 20 15
35 35
70
70
Zasada tworzenia powyższego diagramu jest analogiczna do zasady tworzenia liczb w trójkącie Pascala: liczba w następnym rzędzie jest sumą dwóch liczb stojących nad nią. Rozwiązanie to nie wymaga bezpośrednio użycia kalkulatora, ale z pewnością wymaga algorytmicznego myślenia.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
