Zad. 1. Prostokąt, którego boki mają długości 8 cm i 18 cm, podziel na dwie części tak, aby można z nich było złożyć kwadrat.W odpowiedzi przyślij zdjęcie lub skan rysunku.
Zad. 2. Jeżeli między cyfry pewnej liczby dwucyfrowej wpiszemy cyfrę 0, to liczba ta wzrośnie dziewięciokrotnie. Jaka to liczba?
Zad. 3. W torebce jest mniej niż 100 cukierków. Ile ich jest dokładnie, jeżeli wiadomo, że można je podzielić po równo między piątkę albo szóstkę dzieci. Natomiast gdyby je podzielić między siedmioro dzieci, to jedno z nich dostałoby o 3 cukierki mniej od każdego z pozostałych.
W lutym punkty zdobyli:
• 3 pkt. – Hanna Cicha OSM Wrocław, Jakub Malicki SP Kobierzyce, Amelia Gugała SP Wrzosów, Sandra Łuczak SP 107 Wrocław, Jan Wojciechowski SP 3 Syców, Alicja Kaliszewska ZSP 1 Brzeg Dolny, Aleksandra Wiercińska SP Raszówka, Aleksander Porębny SP 113 Wrocław, Joanna Nowakowska SP 3 Głogów, Paulina Hołodniuk SP 2 Wołów, Piotr Musielak SP 3 Ścinawa, Igor Rączkiewicz SP Lewin Brzeski, Daria Dziedzic SP 107 Wrocław, Marta Goch SP 17 Wrocław, Grzegorz Kędzior SP 4 Warszawa, Oliwia Urbanek SP 6 Brzeg, Michał Sofiński SP 3 Syców, Justyna Kładoczna SP 118 Wrocław, Zuzanna Buraczewska SP 107 Wrocław, Alicja Szwarczyńska SP Kowalowa, Filip Nowak SP 1 Wołów, Marian Stawowy Salezjańska SP Wrocław i Tymoteusz Noremberg SP 29 Wrocław i Antoni Adamus SP 4 Warszawa, Szymon Grech Niepubliczna SP Koszarawa Bystra, Miłosz Zakrzewski SP Gostycyn;
• 2 pkt. – Andrzej Nowak SP 2 Oborniki Śląskie,Dawid Stępień SP 15 Opole, Weronika Kiniorska SP 118 Wrocław, Jan Rosiek SP 3 Syców, Emilia Cichowska SP 14 Lubin, Mateusz Misztal SP 5 Kielce, Aleksander Jeziorny SP 3 Syców, Paweł Szwarocki SP Jedlnia letnisko, Anna Paszkiewicz SP 6 Świdnica, Tymon Srokosz SP 52 Warszawa i Zuzanna Lipka SP Jedlnia-Letnisko.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
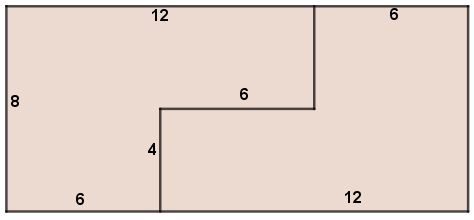
Zad. 1. Pole kwadratu musi wynosić 8 ·18 = 144 cm2, czyli jego bok ma 12 cm. Możliwe rozwiązanie przedstawia rysunek.
Zad. 2. Niech x - cyfra dziesiątek, y - cyfra jedności szukanej liczby. Wówczas liczba dwucyfrowa ma wartość 10x +y, a trzycyfrowa 100x + y. Zgodnie z warunkami zadania 100x + y=9(10x + y), skąd 5x = 4y. Liczba y zatem jest podzielna przez 5, czyli y = 5 lub y = 0. W pierwszym wypadku x = 4. W drugim nie otrzymamy liczby dwucyfrowej. Szukana liczba to 45.
Zad. 3. Liczba cukierków jest podzielna przez 5 i przez 6, więc jest podzielna przez 30 (bo 5 i 6 są względnie pierwsze!). Cukierków w torebce jest więc 30, 60 lub 90. Z tych liczb tylko 60 warunek zadania, gdyż 60 + 3 jest podzielne przez 7. W torebce jest 60 cukierków.
