Zad. 1. Liczba samochodów wyprodukowanych w pewnej fabryce zmniejszyła się w stosunku do poprzedniego roku o 10%. W poprzednim roku sedany stanowiły 50% wyprodukowanych w tej fabryce samochodów, a w kolejnym roku aż 55%. Oblicz, o ile procent w porównaniu z poprzednim rokiem zwiększyła się lub zmniejszyła liczba wyprodukowanych w tej fabryce sedanów.
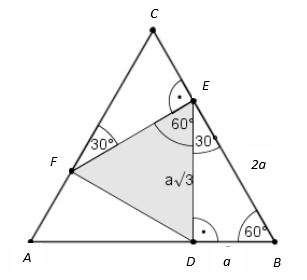
Zad. 2. W trójkąt równoboczny ABC wpisano trójkąt równoboczny DEF w taki sposób, że boki AB i DE są prostopadłe, a wierzchołek F leży na boku AC. Oblicz, ile razy pole trójkąta DEF jest mniejsze od pola trójkąta ABC.
Zad. 3. Dana jest liczba trzycyfrowa [tex]\overline{xyz}[/tex], której potrojona suma cyfr wynosi 42. Jeżeli do liczby [tex]\overline{xyz}[/tex] dodamy 297, to otrzymamy też liczbę trzycyfrową, ale o cyfrach zapisanych w odwrotnej kolejności; natomiast jeśli od podwojonej sumy cyfr setek i dziesiątek liczby [tex]\overline{xyz}[/tex] odejmiemy 7, to otrzymamy cyfrę jedności tej liczby. Jaka to liczba?
W lutym punkty zdobyli:
- 3 pkt. – Dominik Bysiewicz I LO Krosno, Adrian Chudzik I LO Leszno, Karol Czub II LO Oleśnica, Bartosz Kaczor I LO Głogów, Mikołaj Mosiak II LO Oleśnica, Laura Stefanowska KLO Legnica, Aleksandra Strzelecka VIII LO Poznań, Wojciech Szwarczyński II LO Wałbrzych, Igor Wojtun I LO Głogów, Kacper Woszczek II LO Wałbrzych;
- 2,5 pkt. – Roman Szlachtun LO 9 Wrocław;
- 2 pkt. – Wiktoria Malinowska XXVII LO Warsza, Kasper Radom II LO Lubin, Gabriela Wołynko I LO Węgrów;
- 1 pkt. – Szymon Kowalcze ZSE Brzeg.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Oznaczmy przez x liczbę samochodów wyprodukowanych w I roku. Wiemy, że 0,9x to liczba samochodów wyprodukowanych w II roku, 0,5x to liczba sedanów wyprodukowanych w I roku, a 0,55⋅0,9x = 0,495x to liczba sedanów wyprodukowanych w II roku. Liczba wyprodukowanych sedanów zmniejszyła się zatem o 0,5x – 0,495x/0,5 . 100% = 1%.
Zad. 2. Niech |DB|=a. Wówczas |BE|=2a oraz |ED|=a√3. Pole trójkąta DEF wynosi [tex]\frac{3a^2\sqrt{3}}{4}[/tex]. Na podstawie cechy przystawania trójkątów kbk trójkąty DBE, CEF i AFD są przystające, więc |CE| = |DB| = a, a pole trójkąta ABC wynosi [tex]\frac{9a^2\sqrt{3}}{4}[/tex]. Pole trójkąta DEF jest 3 razy mniejsze od pola trójkąta ABC.
Zad. 3. Z treści zadnia otrzymujemy układ trzech równań: 3(x+y+z) = 42, 100x+10y+z+297 = 100z+10y+x oraz 2(x+y)–7 = z. Po rozwiązaniu otrzymujemy spełniającą go trójkę (4, 3, 7), czyli szukaną liczbą jest 437.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
