Zad. 1. Wszystkie cyfry pewnej liczby czterocyfrowej będącej kwadratem liczy naturalnej można zmniejszyć o tę samą liczbę, tak że powstanie liczba czterocyfrowa też będąca kwadratem liczby naturalnej. Znajdź wszystkie takie liczby czterocyfrowe.
Zad. 2. W trójkącie ABC poprowadzono dwusieczne AD i BE (D ∈ BC, E ∈ AC) przecinające się w punkcie O. Wiadomo, że OE = 1 i wierzchołek C leży na okręgu przechodzącym przez punkty E, D i O. Znajdź miary kątów i boków trójkąta EDO.
Zad. 3 Ile jest liczb mniejszych od 10 000 postaci 8m + 5n, gdzie m, n ∈ N, których zapis dziesiętny kończy się cyfrą 1?
W lutym punkty zdobyli:
- 3 –Emilia Cichowska II LO Lubin, Wojciech Domin III LO Wrocław, Rafał Górzyński I LO Lubin, Wiktoria Prokop II LO Głogów, Wojciech Raszczuk I LO Bolesławiec, Karolina Szymandera I LO Inowrocław, Michał Węgrzyn ALO PWr Wrocław;
- 2 – Adam Chowanek III LO Wałbrzych, Karol Czajka II LO Oleśnica, Igor Wojtasik I LO Jelenia Góra.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech m2 – liczba początkowa czterocyfrowa, n2 – liczba otrzymana zgodnie z warunkami zadania. Wówczas m2-n2=1000x+100x+10+x=101.11.x, gdzie x – liczba jednocyfrowa, stąd (m-n)(m+n)= 101.11.x. Ponadto m<100, bo m2<1002=10 000, więc m-n<100 i m+n<200, czyli m+n=101 i m-n=11.x. Z pierwszego równania wynika, że jedna z liczb jest parzysta a druga nieparzysta, więc x jest nieparzyste. Mamy, więc
[tex] \left\{\begin{array}{rcl}m+n&=&101\\m-n&=&11\end{array}\right. lub \left\{\begin{array}{rcl}m+n&=&101\\m-n&=&33\end{array}\right. lub \left\{\begin{array}{rcl}m+n&=&101\\m-n&=&55\end{array}\right. lub \left\{\begin{array}{rcl}m+n&=&101\\m-n&=&77\end{array}\right. lub \left\{\begin{array}{rcl}m+n&=&101\\m-n&=&99\end{array}\right. [/tex]
skąd otrzymujemy
[tex] \left\{\begin{array}{rcl}m&=&56\\n&=&45\end{array}\right. lub \left\{\begin{array}{rcl}m&=&67\\n&=&34\end{array}\right. lub \left\{\begin{array}{rcl}m&=&78\\n&=&23\end{array}\right. lub \left\{\begin{array}{rcl}m&=&89\\n&=&12\end{array}\right. lub \left\{\begin{array}{rcl}m&=&100\\n&=&1\end{array}\right. [/tex]
Tylko pierwszy i drugi układ spełnia warunki zadania, gdyż n2 jest liczbą czterocyfrową, czyli n2≥1000. Szukane liczby to 562=3136 i 672=4489
Zad. 2. Dwusieczne kątów trójkąta przecinają się w jednym punkcie, zatem odcinek CO jest zawarty w dwusiecznej kąta C trójkata ABC, czyli ∠ECO=∠DCO=α (rys. 1). Kąty wpisane oparte na tym samym łuku są równe, a stąd =∠OED=α i =∠ODE=α. Szukamy miary kąta EOD trójkąta EDO. ∠EOD=1800-2α=∠AOB=1800-1/2(A+B)=1800-1/2 (1800-2α)=900+α, czyli 1800-2α=900+α, α=300. W trójkącie EOD mamy więc: ∠E=∠D=300, ∠O=1200. OE=OD=1. Bok ED jest równy podwojonej wysokości w trójkącie równobocznym o boku 1 (rys. 2). [tex] ED=2\cdot\frac{\sqrt{3}}{2}=\sqrt{3} [/tex].
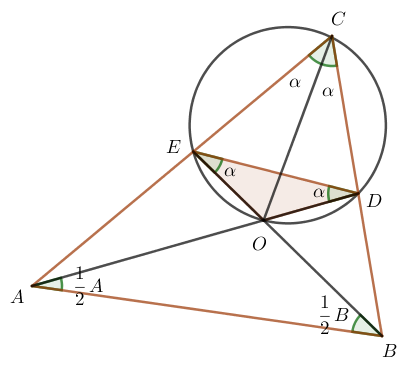rys. 1 
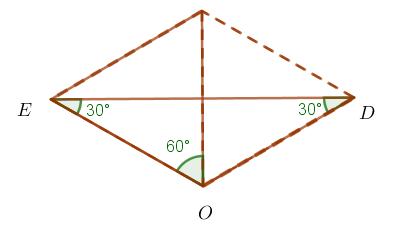rys.2
Zad. 3. Liczba 5n ma w zapisie dziesiętnym cyfrę jedności 5, dla n ∈ N i n ≠0. Liczba 8n kończy się zatem cyfrą 6, bo tylko wtedy zapis dziesiętny liczby 8m + 5n kończy się cyfrą 1. Zauważmy teraz, że 81=8, 82=64 , 83=512, 84=4721 , 85>10 000, m może więc przyjąć tylko wartość 4. Teraz mamy 84 + 51 = 4101, 84 + 52 = 4121, 84 + 53 =4221, 84 + 54 = 4721, 84 + 55 = 7221, 84 + 56 > 10 000. Liczb spełniających warunki zadania jest 5. Gdyby liczbę 0 przyjąć za liczbę naturalną odpowiedź nie zmieni się (dlaczego?).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
