Zad. 1. Zastęp harcerzy zaplanował przejechanie na rowerach trasy 360 km, każdego dnia takiej samej długości. Jednak faktycznie przejechali każdego dnia o 4 km mniej niż zaplanowano i z tego powodu wycieczka przedłużyła się o 3 dni. Ile dni wg planu miała trwać wycieczka?
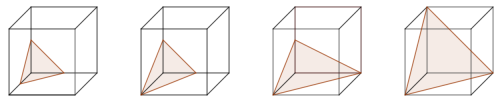
Zad. 2. Drewniany sześcian rozcieto płaszczyzną na dwa wielościany, z których jeden ma 6 krawędzi a drugi 15. Ile wierzchołków ma każdy z nich?
Zad. 3. Jakie są miary kątów trójkąta równoramiennego, w którym dwusieczna jednego z kątów odcina od trójkąta nowy trójkąt równoramienny?
W marcu punkty zdobyli:
- 3 – Wojciech Raszczuk I LO Bolesławiec, Wiktoria Prokop II LO Głogów, Karolina Szymandera I LO Inowrocław;
- 2,5 – Karol Czajka II LO Oleśnica, Igor Wojtasik I LO Jelenia Góra
- 2 – Emilia Cichowska II LO Lubin, Wojciech Domin III LO Wrocław, Rafał Górzyński I LO Lubin, Monika Rębacz, Michał Węgrzyn ALO PWr Wrocław;
- 1 – Hubert Kosmala II LO Oleśnica.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech x to liczba kilometrów zaplanowana na jeden dzień, a y - liczba zaplanowanych dni wycieczki. Możemy zapisać układ równań: xy = 360 i (x–4)(y+3) = 360. Po rozwiązaniu tego układu otrzymamy x = 24 i y = 15, zatem wycieczka miała trwać 15 dni.
Zad. 2. Wielościan, który ma 6 krawędzi, jest czworościanem. Od sześcianu można odciąć czworościan na cztery sposoby, jak pokazano na rysunku poniżej (dlaczego innych możliwości nie ma?). Druga część ma wówczas odpowiednio 15, 14, 13 lub 12 krawędzi. Warunki zadania spełnia tylko cięcie pokazane na pierwszym diagramie. Jedna część ma wówczas 4 wierzchołki, a druga - 10.
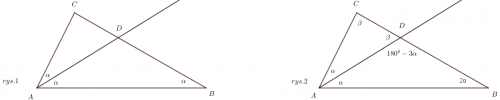
Zad. 3. Rozważmy dwa przypadki.
A) Jeśli odcięty trójkąt ABD jest równoramienny (rys. 1 poniżej), to ponieważ trójkąt ABC był równoramienny, zachodzi |∡BCA| = 2α lub |∡BCA| = α (dlaczego tylko te przypadki są możliwe?). Stąd otrzymujemy α = 36° lub α = 45°, co daje możliwe trójkąty o kątach (36°, 72°, 72°) albo (45°, 45°, 90°).
B) Jeśli odcięty trójkąt ACD jest równoramienny (rys. 2 poniżej), to jedynym nowym przypadkiem jest |∡ADC| = |∡DCA| = (180–α)/2 oraz |∡ABC| = 2α (dlaczego nie ma innych możliwości?). Wówczas |∡BDA| = 180°–3α, a stąd β = 3α. Otrzymamy wówczas trójkąt o kątach 3/7·180°, 2/7·180°, 2/7·180°, czyli (771/7°, 513/7°, 513/7°).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
