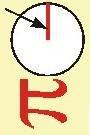
Zad. 1. Narysowano 2023-kąt foremny. Wszystkie wierzchołki oraz środki boków podpisano liczbami naturalnymi od od 1 do 4046, przy czym każdej użyto dokładnie raz. Czy jest możliwe, by dla każdego boku suma trzech liczb przypisanych jego końcom i środkowi była taka sama?
Zad. 2. Wszystkie liczby naturalne dodatnie pokolorowano na zielono lub na czerwono, przy czym suma trzech jednokolorowych liczb również ma ten kolor. Ile jest możliwych kolorowań spełniających ten warunek?
Zad. 3. Dla jakich liczb naturalnych n liczba n2+1 jest dzielnikiem n7+13?
Za nadesłane rozwiązania nie przyznano punktów.
Zad. 1. Zapiszmy na środkach kolejnych boków wielokąta kolejne liczby parzyste. Suma wszystkich sum będzie wówczas uwzględniać liczby parzyste jednokrotnie, a nieparzyste dwukrotnie. Jako że [(2+4+...+4046)+2·(1+3+...+4045)]/2023 = 6070, suma liczb leżących na każdym boku musi wynosić właśnie 6070. Liczbę 1 wstawiamy pomiędzy dwie największe liczby parzyste. Pozwala to ustalić liczbę, jaką należy przyporządkować kolejnym wierzchołkom, zaczynając od prawego sąsiada jedynki. Jak nietrudno zauważyć, otrzymamy dwa rosnące ciągi arytmetyczne liczb nieparzystych, które po okrążeniu całego wielokąta będą wciąż spełniać warunki zadania, nawet w jedynym potencjalnie newralgicznym miejscu, jakim jest lewa strona wpisanej jedynki.
Zad. 2. Załóżmy bez straty ogólności, że jedynka jest zielona. Wówczas dla każdej liczby nieparzystej n kolejna liczba nieparzysta n+1+1 również musi być zielona. Gdyby dwójka była zielona, każda liczba parzysta także musiałaby mieć ten kolor.
Jeśli zaś dwójka jest czerwona, to każda liczba parzysta niepodzielna przez cztery (n+2+2) też. Jednak czwórka nie może być zielona – wtedy 6 = 4+1+1 miałaby kolor zielony, co stanowi sprzeczność z poprzednim zdaniem. Wobec tego każda wielokrotność czwórki jest czerwona.
Analogiczne rozumowanie przeprowadzamy dla czerwonej jedynki, otrzymując w sumie cztery kolorowania.
Zad. 3. Dzielimy z resztą n7+13 przez n2+1, otrzymując rozkład n7+13 = (n2+1)(n5–n3+n)–n+13. Podzielność n7+13 przez n2+1 jest więc równoważna podzielności –n+13 przez n2+1. Warunkiem koniecznym do tego jest –n+13 ≥ n2+1 lub –n+13=0. Po przekształceniu tych warunków do sprawdzenia pozostaną tylko liczby: 1, 2, 3, 13. Warunki zadania spełniają 1, 3, 13.