Zad. 1. Wyznacz wszystkie pary liczb naturalnych m, n, dla których liczba √m–√n jest wymierna.
Zad. 2. Czy dwa kolejne wyrazy ciągu Fibonacciego mogą nie być względnie pierwsze?
Zad. 3. Na trójwymiarowej szachownicy 2023 × 2023 × 2023 niektóre pola zostały zarażone. Co minutę każde pole, które sąsiaduje (przez wspólną ścianę) z przynajmniej trzema zarażonymi, również zostaje zainfekowane. Ile co najwyżej pól mogło zostać zarażonych na początku, żeby można było mieć pewność (niezależnie od wyboru tych pól), że przynajmniej jedno pole nigdy nie zostanie zainfekowane?
Uwaga! Tak jak szachownica dwuwymiarowa to kwadrat podzielony na kwadraciki, tak szachownica trójwymiarowa to sześcian podzielony na sześcianiki.
W bieżącym miesiącu nie przyznano punktów.
Zad. 1. Zapiszmy liczby m i n odpowiednio jako a2b oraz c2d, gdzie w rozkładzie na czynniki pierwsze liczb b i d każdy występuje co najwyżej raz. Skoro √m–√n ma być wymierne, to √(a2b)–√(c2d) = p/q dla pewnych całkowitych p i q. Po podniesieniu do kwadratu otrzymamy a2b + c2d – 2ac√(bd) = p2/q2, a po przeniesieniu wszystkiego poza pierwiastkiem na prawą stronę: (bd) = [skomplikowane wyrażenie, które na pewno jest liczbą wymierną]. Jeśli pierwiastek z liczby jest wymierny, to ta liczba musi być kwadratem. Oznacza to, że w rozkładzie na czynniki pierwsze każdy czynnik występuje w niej parzyście wiele razy. Ale w b i d każdy występuje co najwyżej raz. Oznacza to, że b = d. Zatem analizowana wyżej równość przyjmuje postać √(a2b)–√(c2b) = p/q, a więc równoważnie (a–c)√b=p/q, czyli √b=p/q(a–c). Liczba b musi więc być kwadratem. Muszą nimi więc być również liczby m i n. Zatem liczby naturalne spełniające warunki zadania to dokładnie kwadraty.
Zad. 2. Niech an, an+1 będą najmniejszą parą kolejnych elementów ciągu Fibonacciego niebędących liczbami względnie pierwszymi. Oznacza to, że mają wspólny dzielnik większy od 1. Ale liczba an–1 = an+1– an także musi dzielić się przez ten dzielnik. Stanowi to sprzeczność, bowiem zakładaliśmy, że an, an+1 to najmniejsza taka para.
Zad. 3. Zauważmy, że zainfekowanie 20232 sześcianików w sposób przedstawiony na obrazku (narysowano na nim kolejne warstwy sześcianu) spowoduje zakażenie całej szachownicy. Pokażemy, że nie można użyć mniejszej ich liczby.
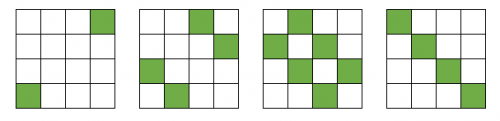
Policzmy, ile ścian sześcianików stanowi granicę pomiędzy obszarami zarażonym i niezarażonym. Na początku takich granic jest co najwyżej 6·(20232–1), jednak w każdej turze liczba granic nie zmienia się lub się zmniejsza. Wobec tego nigdy nie dojdziemy do sytuacji, w której wszystkie komórki są zainfekowane, bowiem wtedy liczba granic wynosiłaby 6·20232.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
