Uwaga! Rozpoczynając od stycznia 2014, zadania Ligi Zadaniowej dla szkół ponadgimnazjalnych należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Oblicz prawdopodobieństwo, że losowo wybrana liczba naturalna ze zbioru {1, 2,…, 1050} jest podzielna przez 3, 5 lub 7.
Zad. 2. Oblicz sumę 2014 początkowych liczb naturalnych, które przy dzieleniu przez 7 dają resztę 2.
Zad. 3. W czworościanie dwie skośne krawędzie mają długość po 4√2 cm, a pozostałe - długość 5 cm. Oblicz objętość tego ostrosłupa.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Kamila Bojar ZSP Szprotawa, Robert Czwartosz LO Trzebnica, Piotr Dzierza XIII LO Wrocław i Tomasz Stempniak I LO Ostrów Wielkopolski,
- 2,75 pkt. - Maciej Golec IX LO Wrocław,
- 2 pkt. - Marcin Korona XIV LO Warszawa,
- 1 pkt. - Krzysztof Bednarek III LO Wrocław i Krzysztof Danielak I LO Jelenia Góra.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Po ośmiu miesiącach Ligi z wynikiem 23,5 pkt. (na 24 możliwe!) prowadzi Robert Czwartosz z LO w Trzebnicy. Gratulujemy!
Zad. 1. Niech A, B, C to zdarzenia polegające na tym, że losowo wybrana liczba naturalna ze zbioru {1, 2, …, 1050} jest podzielna odpowiednio przez 3, 5 i 7. Szukane jest prawdopodobieństwo P(AυBυC). Prawdopodobieństwo sumy trzech zdarzeń jest równe
P(AυBυC) = P(A) + P(B) + P(C) - P(A∩B) - P(B∩C) - P(A∩C) + P(A∩B∩C)
(co wynika z zasady włączeń i wyłączeń, a jej prawdziwość można sprawdzić korzystając z diagramów Venna).
W tym przypadku P(AυBυC) = 1/3 + 1/5 + 1/7 - 1/15 - 1/35 - 1/21 + 1/105 = 19/35.
Zad. 2. Szukane liczby są wyrazami ciągu arytmetycznego an = 2+(n-1)·7, dla n = 1, 2, ..., 2014.
Ich suma wynosi (a1+a2014)·2014/2 = 14 193 665.
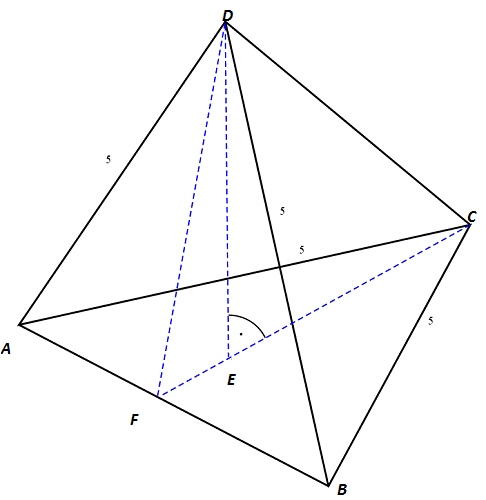
Zad. 3. Niech E będzie spodkiem wysokości ostrosłupa ABCD opuszczonej z wierzchołka D. Trójkąty ABC i ABD są równoramienne i przystające oraz mają wspólną podstawę AB, zatem E leży na odcinku CF, gdzie F jest środkiem krawędzi AB. Jesli krawędzie AB i CD mają długość 4√2 cm, to z twierdzenia Pitagorasa dla trójkąta CBF mamy |CF| = |DF| = √17 cm. Następnie stosujmy twierdzenie Pitagorasa do trójkątów CDE i DEF, otrzymując równania 32 = |CE|2 + |DE|2 oraz 17 = (√17-|CE|)2 + |DE|2.
Rozwiązując je, dostaniemy |CE| = 16/√17 cm oraz |DE| = 12√2/√17 cm.
Objętość ostrosłupa wynosi V = 1/3·PΔABC·|DE| = 1/3·1/2·4√2·√17·12√2/√17 = 16 cm3.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
