Uwaga! Rozpoczynając od stycznia 2014, zadania Ligi Zadaniowej dla szkół ponadgimnazjalnych należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Oblicz 1/1·2 + 1/2·3 + 1/3·4 + … + 1/2013·2014 .
Zad. 2. Udowodnij, że dla każdej liczby naturalnej n liczba 2n3+6n2+n+12 jest podzielna przez 3.
Zad. 3. Na powierzchni sześcianu o krawędzi a znajdź symetralną jednej z jego przekątnych, tzn. wszystkie punkty jednakowo odległe od końców tej przekątnej.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Krzysztof Bednarek III LO Wrocław, Kamila Bojar ZSP Szprotawa, Robert Czwartosz LO Trzebnica, Maciej Golec IX LO Wrocław i Tomasz Stempniak I LO Ostrów Wielkopolski,
- 2,5 pkt. - Marcin Korona XIV LO Warszawa,
- 2 pkt. - Krzysztof Danielak I LO Jelenia Góra, Piotr Dzierza XIII LO Wrocław i Antoni Kamiński III LO Wrocław.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Po siedmiu miesiącach Ligi z wynikiem 20,5 pkt. (na 21 możliwych!) prowadzi Robert Czwartosz z LO w Trzebnicy. Gratulujemy!
Zad. 1. Wystarczy zauważyć, że każdy ze składników sumy jest różnicą dwóch ułamków: 1/n·(n+1) = 1/n - 1/(n+1). Po zastosowaniu tego faktu dostaniemy
1/1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 +…+ 1/2013 - 1/2014 = 1 - 1/2014 = 2013/2014.
Zad. 2. Zapiszmy 2n3+6n2+n+12 jako n(2n2+1)+3(2n2+4). Drugi składnik jest oczywiście podzielny przez 3. Wystarczy więc pokazać, że pierwszy składnik też. Rozpatrzmy kolejno przypadki, że n daje z dzielenia przez 3 reszty 0, 1 lub 2, czyli że zachodzi odpowiednio n=3m, n=3m+1 lub n=3m+2, gdzie m jest dowolną liczbą naturalną. W pierwszym przypadku liczba n(2n2+1) jest oczywiście podzielna przez 3. W drugim przypadku dostajemy (3m+1)·(2(3m+1)2+1) = (3m+1)·(18m2+12m+3) i widać, że drugi czynnik dzieli się przez 3. W trzecim przypadku dostajemy (3m+2)·(2(3m+2)2+1) = (3m+2)·(18m2+24m+9) i znowu drugi czynnik dzieli się przez 3, co kończy dowód.
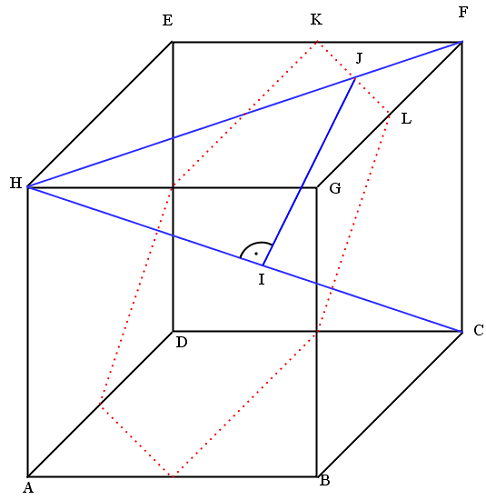
Zad. 3. W przestrzeni symetralną odcinka (czyli zbiorem punktów równoodległych od końców tego odcinka) jest płaszczyzna prostopadła do odcinka i przechodząca przez jego środek. Zatem szukamy punktów przecięcia z sześcianem płaszczyzny prostopadłej do jego przekątnej, przechodzącej przez środek sześcianu (na rys. punkt I). Weźmy sześcian ABCDEFGH. Pokażemy, że płaszczyzna prostopadła do jego przekątnej w punkcie I przechodzi przez środki krawędzi EF i FG, tworząc odcinek KL na ścianie EFGH. Powtarzając analogiczne rozumowanie do pozostałych ścian sześcianu, znajdziemy przecięcie symetralnej z powierzchnią sześcianu.
Trójkąty CFH i HIJ są podobne z cechy k-k-k, zatem mają jednakowy stosunek długości przeciwprostokątnej do dłuższej przyprostokątnej, czyli CH/HF = HJ/HI, tzn. a√3/a√2 = HJ/a√3/2. Stąd HJ = 3a√2/4. Dalej FJ = HF-HJ = a√2 - 3a√2/4 = a√2/4. Ponadto FJ jest wysokością prostokątnego trójkąta równoramiennego FKL opuszczoną na przeciwprostokątną KL, czyli jest od niej dwa razy krótsza (dlaczego?). Daje to KL = 2·FJ = a√2/2. Stąd i z twierdzenia Pitagorasa dostajemy, że przyprostokątne trójkąta FKL mają długość KF = LF = a/2, zatem rzeczywiście są połówkami krawędzi sześcianu.
Powtarzając to rozumowanie dla pozostałych ścian widzimy, że na każdej z nich płaszczyzna symetralna przechodzi przez środki krawędzi. Zatem szukaną figurą jest sześciokąt równoboczny o boku a√2/2 (na rysunku zaznaczony kolorem czerwonym). Jeśli zauważymy, że dłuższe przekątne tego sześciokąta są jednakowe (równe a√2), to okaże się, że jest to sześciokąt foremny (dlaczego)? Zatem zbiorem punktów na powierzchni sześcianu równoodległych od końców jego przekątnej jest sześciokąt foremny przechodzący przez środki sześciu krawędzi sześcianu.
Rozwiązanie zad. 2
Lepiej zapisać tę liczbę jako 3n3+6n2+12-(n3-n) = 3n3+6n2+12-n(n-1)(n+1) i wszystko jasne.
Zadanie 2
Bardzo trafne spostrzeżenie!