Zad. 1. Awaria jednej z komputerowo sterowanych tokarek CNC (ang. Computerized Numerical Control) spowodowała wyłączenie bezpiecznika w rozdzielni elektrycznej doprowadzającej prąd do n tokarek pracujących w fabryce silników wysokoprężnych w Andrychowie. Jakie jest prawdopodobieństwo, że trzeba będzie sprawdzić m≤n tokarek, aby usunąć awarię, jeśli uszkodzenia poszczególnych tokarek są zdarzeniami niezależnymi?
Zad. 2. Rozwiąż równanie: [tex]2015^{|1-4x^2|}=\sin(\pi x)[/tex].
Zad. 3. Niech R i r będą promieniami kul odpowiednio opisanej na ostrosłupie prawidłowym czworokątnym i wpisanej w ten ostrosłup. Udowodnij, że R/r ≥ 1+√2.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Robert Czwartosz LO Trzebnica, Bartosz Czyżewski I LO Jelenia Góra, Piotr Paduszyński SLO Żary, Tomasz Stempniak I LO Ostrów Wielkopolski i Wojciech Wiśniewski I LO Giżycko;
- 2 pkt. - Kamila Bojar ZSP Szprotawa;
- 1 pkt. - Dawid Hanrahan I LO Brzeg, Szymon Meyer II LO Opole i Marta Włóczyk OSSP Opole.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Po ośmiu miesiącach Ligi Zadaniowej z wynikiem 23,5 pkt. (na 24 możliwych) prowadzi Tomasz Stempniak, drugie miejsce z wynikiem 23 pkt. zajmuje Bartosz Czyżewski, a trzecie z wynikiem 22,5 pkt. - Piotr Paduszyński. Gratulujemy!
Zad. 1. To, że aby usunąć awarię, trzeba sprawdzić m≤n tokarek, oznacza, że najpierw sprawdzimy m-1 działających tokarek, a następnie trafimy na tokarkę zepsutą. Prawdopodobieństwo takiego zdarzenia wynosi (n-1)/n · (n-2)/(n-1) · ... · (n-m)/(n-m+1) · 1/(n-m) = 1/n.
Zad. 2. Ponieważ zbiorem wartości lewej strony równania jest [1;+∞), a zbiorem wartości prawej strony jest jest [-1;1], możliwe pierwiastki są takie, dla których wartością jest liczba 1. Lewa strona równania przyjmuje wartość 1 dla x=-1/2 i x=1/2, a prawa strona - dla x = 1/2+2kπ, gdzie k jest liczbą całkowitą. Stąd widać, że jedynym pierwiastkiem równania jest 1/2.
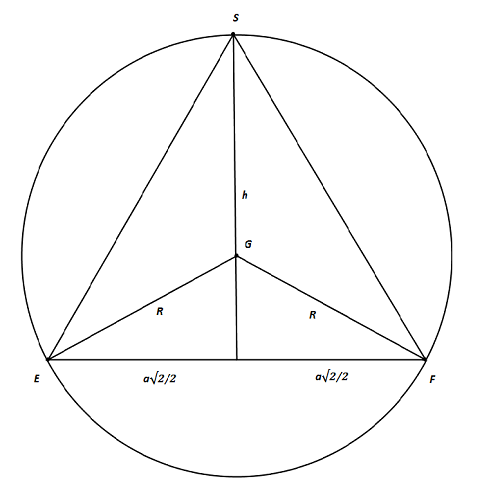
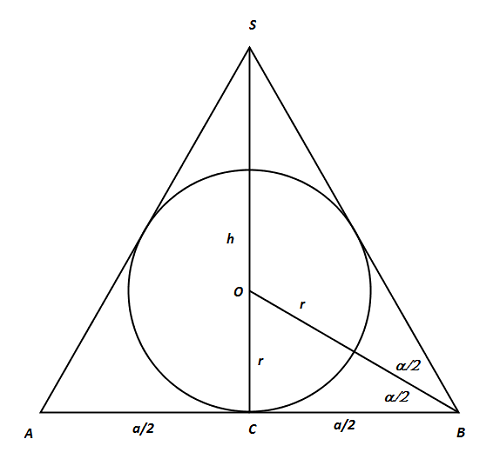
Zad. 3. Zauważmy, że r = a/2·tgα/2 i h = a/2·tgα. Promień okręgu opisanego na trójkącie jest równy iloczynowi długości boków podzielonemu przez czterokrotność pola tego trójkąta.
Stąd [tex]R=\frac{a\sqrt{2}\left(\sqrt{h^2+\frac{a^2}{2}}\right)^2}{2a\sqrt{2}h}[/tex], a po uproszczeniu [tex]R=0,5\left(h+\frac{a^2}{2h}\right)=\frac{a}{2}\left(0,5\text{tg}\alpha+\text{ctg}\alpha\right)[/tex].
Dzieląc stronami przez r, dostaniemy [tex]\frac{R}{r}=\frac{1}{1-\text{tg}^2\frac{\alpha}{2}}+\frac{1-\text{tg}^2\frac{\alpha}{2}}{2\text{tg}^2\frac{\alpha}{2}}[/tex].
Podstawiając [tex]x=\text{tg}^2\frac{\alpha}{2}[/tex], ponieważ 0< α/2 < π/4, mamy 0<x<1
i wystarczy udowodnić, że [tex]\frac{1}{1-x}+\frac{1-x}{2x}\geq 1+\sqrt{2}[/tex].
Tą nierówność można przekształcić do postaci [tex]((1+\sqrt{2})x-1)^2\geq 0[/tex], co kończy dowód.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
