Jednym ze sposobów graficznej ilustracji zebranych danych jest sporządzenie histogramu. Histogram to wykres słupkowy, na którym wysokość danego słupka odpowiada liczbie obserwacji, które znalazły się w przedziale, nad którym narysowany jest słupek. Często zamiast liczby obserwacji zaznacza się, jaka część wszystkich obserwacji znajduje się w danym przedziale, nad którym narysowany jest słupek. (O histogramach pisaliśmy szerzej w poprzednim roku szkolnym).
Dwa poniższe histogramy przedstawiają dane o wzroście 51 studentek matematyki na Uniwersytecie Wrocławskim (wykres po lewej) i 62 studentów matematyki na Uniwersytecie Wrocławskim (wykres po prawej). Dane zostały zebrane na potrzeby dydaktyczne od studentów przypadkowo spotkanych na korytarzu Instytutu Matematycznego Uniwersytetu Wrocławskiego.
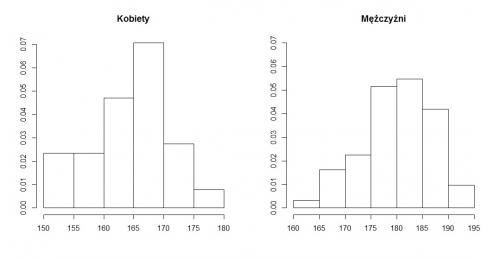
Widzimy, że oba histogramy układają się w dość charakterystyczny kształt: na środku słupki są najwyższe i stopniowo obniżają się, gdy rozważamy przedziały położone coraz bardziej na lewo oraz coraz bardziej na prawo na osi liczbowej.
Taki rozkład danych jest powszechnie spotykany w wielu zagadnieniach przyrodniczych i nie tylko. Bardzo znaczna część obserwowanych przez ludzi danych ma właśnie taką strukturę. Matematycznym modelem takich zjawisk jest rozkład normalny, któremu poświęcimy niniejszy odcinek ligi.
W listopadzie uczyniliśmy rozróżnienie na rozkłady ciągłe i dyskretne. Przypomnijmy, że rozkłady ciągłe to takie, które mają gęstość (jeśli nie pamiętasz, zajrzyj tu). Dla dalszego wywodu nie jest szczególnie ważne, byśmy wiedzieli, jak wygląda wzór na gęstość rozkładu normalnego, ale przedstawimy go dla porządku:
[tex]f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}.[/tex]
W powyższym wzorze oprócz x będącego argumentem funkcji występują jeszcze dwie inne zmienne oznaczone greckimi literami μ (mi) i σ (sigma). μ może być dowolną liczbą rzeczywistą, podczas gdy σ>0. Po wstawieniu do powyższego wzoru za μ i σ konkretnych liczb otrzymujemy gęstość konkretnego rozkładu normalnego. O takim rozkładzie będziemy mówili, że jest to rozkład normalny z parametrami μ i σ i będziemy go oznaczali N(μ,σ). (e we wzorze to pewna stała matematyczna zwana liczbą Eulera, będąca liczbą niewymierną równą w przybliżeniu 2,71. Na Wrocławskim Portalu Matematycznym wspomniano o niej np. tu).
Gęstości rozkładów normalnych mają charakterystyczny kształt, który bywa nazywany dzwonem. Na poniższym wykresie zostały przedstawione gęstości kilku rozkładów normalnych. W legendzie podano wartości parametrów tych rozkładów.
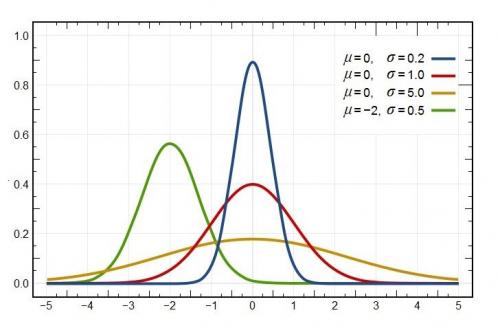
Rzut oka na wykresy pozwala ocenić, jaką rolę dla ich wyglądu odgrywają poszczególne parametry. Parametr μ odpowiada za położenie wykresu gęstości. Gęstość rozkładu normalnego osiąga maksimum w x=μ. Co więcej, wykres jest symetryczny względem prostej x=μ. Im μ jest mniejsze, tym charakterystyczny dzwon położony jest bardziej na lewo, im większe - tym dzwon jest bardziej na prawo w układzie współrzędnych. Z kolei σ decyduje o kształcie dzwonu: im σ mniejsze, tym dzwon jest "chudszy", natomiast im σ jest większe, tym dzwon jest "grubszy", bardziej pękaty (choć niższy).
Mimo że nie mówiliśmy o wartości oczekiwanej i wariancji (a zatem i o odchyleniu standardowym) rozkładów ciągłych a jedynie dyskretnych, to jednak w tym miejscu warto powiedzieć, że w rozkładzie N(μ,σ) wartość oczekiwana jest równa μ, natomiast odchylenie standardowe wynosi σ (a zatem wariancja jest równa σ2). Jeśli rozumiemy znaczenie wartości oczekiwanej, staje się jasne, że im większe μ, tym zmienna losowa o rozkładzie N(μ,σ) przyjmuje większe wartości, natomiast im większe σ, tym zmienna losowa o rozkładzie N(μ,σ) ma większy rozrzut wokół swej wartości oczekiwanej (wynoszącej μ).
Na poniższych rysunkach do histogramów sporządzonych wcześniej dorysowano wykresy gęstości rozkładów normalnych z pewnymi parametrami, tak aby pokazać, że kształt histogramu sporządzonego na podstawie rzeczywistych danych niejednokrotnie daje się przybliżyć za pomocą gęstości rozkładu normalnego. (O tym, jak wybrać owe wartości parametrów do narysowania tych wykresów gęstości, powiemy w przyszłości, aczkolwiek już w zad. 3 dla licealistów pojawia się pewne rozwiązanie tego problemu). Jak widać, dopasowanie jest nie najgorsze, szczególnie gdy chodzi o mężczyzn (choć pewnie byłoby lepsze, gdyby zebrano dane od większej liczby studentów). Przekonuje nas to o tym, że rozkład normalny nadaje się do opisywania zjawisk występujących w przyrodzie (a takim zjawiskiem niewątpliwie jest wzrost człowieka).

Przypomnijmy, że dystrybuantą zmiennej losowej X nazywamy funkcję zadaną wzorem F(t) = P(X≤t), określoną dla każdej liczby rzeczywistej t (o dystrybuancie pisaliśmy w listopadzie).
Dystrybuanta jakiegokolwiek rozkładu normalnego nie daje się jawnie opisać za pomocą żadnych znanych nam funkcji, tak aby można było ręczne obliczyć jej wartości, podstawiając argument do wzoru, toteż sporządza się dla niej tablice podobne do tych dla funkcji trygonometrycznych (gimnazjaliści poznają tablice funkcji trygonometrycznych w szkole ponadgimnazjalnej). Takie tablice są wystarczające, aby efektywnie posługiwać się rozkładem normalnym choćby w zadaniach, jakie dołączone są do tego odcinka ligi.
Warto jeszcze zwrócić uwagę, że jeśli zmienna losowa X ma rozkład ciągły, to dla dowolnej liczby rzeczywistej t zachodzi P(X=t) = 0. Wobec tego
P(X≤t) = P(X<t lub X=t) = P(X<t) + P(X=t) = P(X<t) + 0 = P(X<t).
Innymi słowy jeśli mamy do czynienia z rozkładem ciągłym, to z punktu widzenia prawdopodobieństwa nie ma znaczenia, czy będziemy rozważali zdarzenie X≤t, czy też X<t, bowiem P(X≤t) = P(X<t) = F(t), gdzie F jest dystrybuantą zmiennej losowej X.
Rozkłady normalne są rozkładami ciągłymi, a zatem powyższa obserwacja tyczy się także do nich.
W tym miejscu warto poznać kilka własności rozkładów normalnych.
- Jeśli X~N(μ,σ), to X+a~N(μ+a,σ).
- Jeśli X~N(μ,σ) i c≠0, to cX~N(cμ,|c|σ).
- Jeśli X~N(μ1,σ1), Y~N(μ2,σ2) i zmienne losowe X i Y są niezależne, to X+Y~N(μ,σ), gdzie μ=μ1+μ1 i σ2=σ12+σ22
Szczególne miejsce w matematyce zajmuje rozkład N(0,1) zwany standardowym rozkładem normalnym. Skoro w jego wypadku μ=0, to wykres jego gęstości jest symetryczny względem prostej x=0 czyli gęstość ta jest funkcją parzystą. Z wspomnianych powyżej własności bardzo łatwo jest wywnioskować związek między zmienną losową o rozkładzie N(μ,σ) (z dowolnymi parametrami μ i σ) i zmiennej losowej o rozkładzie N(0,1):
- Jeśli [tex]X\sim N(0,1)[/tex] i [tex]\sigma >0,[/tex] to [tex]\sigma X+\mu\sim N(\mu,\sigma).[/tex]
- Jeśli [tex]X\sim N(\mu,\sigma),[/tex] to [tex]\frac{X-\mu}{\sigma}\sim N(0,1).[/tex]
Aby udowodnić pierwszy związek, wystarczy skorzystać kolejno z drugiej i pierwszej z przytoczonych wcześniej własności:
[tex]X\sim N(0,1) \quad \Rightarrow \quad \sigma X\sim N(0,\sigma) \quad \Rightarrow \quad \sigma X+\mu\sim N(\mu,\sigma).[/tex]
Podobnie należy uczynić, udowadniając drugi związek:
[tex]X\sim N(\mu,\sigma) \quad \Rightarrow \quad X-\mu\sim N(0,\sigma) \quad \Rightarrow \quad \frac{X-\mu}{\sigma}\sim N(0,1).[/tex]
Podobnie można wyprowadzić związek między dystrybuantą zmiennej losowej o rozkładzie N(μ,σ) (z dowolnymi parametrami μ i σ) a dystrybuantą miennej losowej o standardowym rozkładzie normalnym N(0,1). Dystrybuantę zmiennej losowej o rozkładzie N(0,1) zazwyczaj oznacza się dużą grecką literą Φ (fi). Zachodzi zatem następujące twierdzenie:
Niech F będzie dystrybuantą zmiennej losowej o rozkładzie N(μ,σ). Wówczas dla każdej liczby rzeczywistej x zachodzi związek:
[tex]F(x)= \Phi\left(\frac{x-\mu}{\sigma}\right).[/tex]
Jak udowodnić to twierdzenie? Niech X~N(μ,σ). Wówczas pamiętając definicję dystrybuanty, bez trudu możemy napisać:
[tex]F(x)=P(X\leq x)=P\left(\frac{X-\mu}{\sigma}\leq \frac{x-\mu}{\sigma}\right)=\Phi\left(\frac{x-\mu}{\sigma}\right).[/tex]
W ostatnim przejściu wykorzystaliśmy fakt, że przy podanych założeniach [tex]\frac{X-\mu}{\sigma}\sim N(0,1)[/tex].
W związku powyższym twierdzeniem nie trzeba sporządzać odrębnych tablic dystrybuanty rozkładu normalnego dla każdej pary parametrów μ i σ. Wystarczy posługiwać się dystrybuantą standardowego rozkładu normalnego N(0,1).
Nim upowszechniły się komputery osobiste, a zatem jeszcze nie tak dawno temu, jeśli chciało się wykorzystywać w rachunkach dystrybuantę standardowego rozkładu normalnego, nie było innej rady jak tylko korzystać z klasycznej papierowej tablicy. Taką przykładową tablicę można zobaczyć np. tu. Korzysta się z niej w następujący sposób: w pierwszej kolumnie poszukujemy interesującego nas argumentu z dokładnością do jednego miejsca po przecinku, a następnie w pierwszym wierszu szukamy drugiego miejsca po przecinku. Na skrzyżowaniu odpowiedniego wiersza i kolumny odczytujemy interesującą nas wartość. Dla przykładu: jeśli poszukujemy Φ(2,61), to w pierwszej kolumnie odnajdujemy liczbę 2,6, natomiast w pierwszym wierszu odszukujemy liczbę 0,01. Poszukiwana wartość Φ(2,61) wynosi zatem 0,99547. Uważny czytelnik zapyta: a co z argumentami ujemnymi? Przecież one nie są ujęte w tablicy? Tutaj wystarczy się posłużyć związkiem: Φ(-x) = 1-Φ(x). Wobec tego np. Φ(-2,61) = 1-Φ(2,61) = 1-0,99547 = 0,00453.
Powyższe wiadomości wykorzystamy to obliczeń z rozkładem normalnym o dowolnych parametrach.
Przykład 1. Oblicz
a) P(X≤4), jeśli X~N(2,4);
b) P(X<2), jeśli X~N(2,2);
c) P(X>2), jeśli X~N(3,5);
d) P(0<X<3), jeśli X~N(1,2).
Rozwiązanie.
a) [tex]P(X\leq 4)=P\left(\frac{X-2}{4}\leq \frac{4-2}{4}\right)=P\left(\frac{X-2}{4}\leq 0,5\right)[/tex]
Skoro [tex]X\sim N(2,4)[/tex], to zmienna losowa [tex]\frac{X-2}{4}[/tex] ma rozkład [tex]N(0,1)[/tex], a zatem [tex]P(X\leq 4)=P\left(\frac{X-2}{4}\leq 0,5\right)=\Phi(0,5)=0,69146.[/tex]
b) [tex]P(X<2)=P\left(\frac{X-2}{4}\leq \frac{2-2}{4}\right)=P\left(\frac{X-2}{2}\leq 0\right)[/tex]
Skoro [tex]X\sim N(2,2)[/tex], to zmienna losowa [tex]\frac{X-2}{2}[/tex] ma rozkład [tex]N(0,1)[/tex], a zatem [tex]P(X<2)=P\left(\frac{X-2}{2}\leq 0\right)=\Phi(0)=0,5000.[/tex]
c) [tex]P(X>2)=1-P(X\leq 2)=1-P\left(\frac{X-3}{5}\leq\frac{2-3}{5}\right)=1-P\left(\frac{X-3}{5}\leq -0,2\right)[/tex]
Skoro [tex]X\sim N(3,5)[/tex], to zmienna losowa [tex]\frac{X-3}{5}[/tex] ma rozkład [tex]N(0,1)[/tex], a zatem [tex]P\left(\frac{X-3}{5}\leq -0,2\right)=\Phi(-0,2).[/tex] Ostatecznie
[tex]P(X>2)=1-P\left(\frac{X-3}{5}\leq -0,2\right)=1-(1-\Phi(0,2))=\Phi(0,2)=0,57926.[/tex]
Pod koniec rachunku skorzystaliśmy z tożsamości: Φ(-x) = 1-Φ(x).
d) [tex]P(0<X<3)=P\left(\frac{0-1}{2}<\frac{X-1}{2}<\frac{3-1}{2}\right)=P\left(-0,5<\frac{X-1}{2}<1\right)[/tex]
Skoro [tex]X\sim N(1,2)[/tex], to [tex]\frac{X-1}{2}[/tex] ma rozkład [tex]N(0,1)[/tex], a zatem
[tex]P(0<X<3)=P\left(-0,5<\frac{X-1}{2}<1\right)=\Phi(1)-\Phi(-0,5)=[/tex]
[tex]=\Phi(1)-(1-\Phi(0,5))=\Phi(1)+\Phi(0,5)-1=[/tex]
[tex]=0,84134+0,69146-1=0,53280.[/tex]
Pod koniec rachunku skorzystaliśmy z tożsamości: Φ(-x) = 1-Φ(x).
Dziś, gdy używanie komputerów osobistych stało się powszechne, coraz rzadziej korzysta się z tablic rozkładów. Wartość dystrybuanty dowolnego rozkładu normalnego w dowolnym punkcie można bardzo szybko obliczyć np. korzystając z funkcji ROZKŁAD.NORMALNY w arkuszu kalkulacyjnym Excel będącym częścią pakietu Microsoft Office lub też z funkcji o tej samej nazwie w arkuszu kalkulacyjnym Calc będącym częścią pakietu OpenOffice lub LibreOffice. Pierwszym argumentem tej funkcji jest argument dystrybuanty, dla którego wartość chcemy obliczyć, a kolejnymi dwoma parametry μ i σ. A zatem jeśli chcemy obliczyć wartość dystrybuanty rozkładu N(2,4) w punkcie 2,61, to musimy użyć formuły ROZKŁAD.NORMALNY(2,61;2;4). Istnieje też specjalna funkcja służąca do obliczania wartości dystrybuanty rozkładu N(0,1). Jeśli zatem chcemy obliczyć wartość dystrybuanty rozkładu N(0,1) w punkcie 2,61, to możemy napisać ROZKŁAD.NORMALNY.S(2,61) (lub alternatywnie ROZKŁAD.NORMALNY(2,61;0;1)). Zachęcam do tego, by obliczenia z powyższego przykładu skonfrontować z wartościami dystrybuant obliczonymi na komputerze. W tym celu warto przeanalizować kolejny przykład.
Przykład 2. Wykonajmy obliczenia z przykładu 1 w arkuszu kalkulacyjnym. W tym celu należy użyć następujących formuł:
a) ROZKŁAD.NORMALNY(4;2;4) lub ROZKŁAD.NORMALNY((4-2)/4;0;1) lub ROZKŁAD.NORMALNY.S((4-2)/4)
b) ROZKŁAD.NORMALNY(2;2;2) lub ROZKŁAD.NORMALNY((2-2)/2;0;1) lub ROZKŁAD.NORMALNY.S((2-2)/2)
c) 1-ROZKŁAD.NORMALNY(2;3;5) lub ROZKŁAD.NORMALNY((2-3)/5;0;1) lub ROZKŁAD.NORMALNY.S((2-3)/5)
d) ROZKŁAD.NORMALNY(3;1;2)-ROZKŁAD.NORMALNY(0;1;2) lub ROZKŁAD.NORMALNY((3-1)/2;0;1)-ROZKŁAD.NORMALNY((0-1)/2;0;1) lub ROZKŁAD.NORMALNY.S((3-1)/2)-ROZKŁAD.NORMALNY((0-1)/2)
Rozkład normalny ma jeszcze jedną ciekawą własność, która potocznie bywa nazywana regułą trzech sigm. Głosi ona, że jeśli X~N(μ,σ), to P(X∈[μ-3σ,μ+3σ]) jest bliskie 1 (dokładnie wynosi 0,99730). Istotnie jeśli X~N(μ,σ), to
[tex]P(\mu-3\sigma \leq X \leq \mu+3\sigma)=P(-3\sigma \leq X-\mu \leq 3\sigma)=[/tex]
[tex]=P\left(-3\leq \frac{X-\mu}{\sigma} \leq 3\right)=\Phi(3)-\Phi(-3)=\Phi(3)-(1-\Phi(3))=[/tex]
[tex]=2\Phi(3)-1=2 \cdot 0,99865-1=0,99730.[/tex]
Można zatem powiedzieć, że jeśli dane pochodzą z rozkładu N(μ,σ), to właściwie wszystkie obserwacje mieszczą się w przedziale [μ-3σ,μ+3σ]. Jeśli zatem przyglądamy się histogramowi sporządzonemu w oparciu o dane pochodzące z rozkładu normalnego, to możemy się spodziewać, że μ znajduje się na osi X z grubsza w tym miejscu, gdzie dzwon, w którego kształt układa się histogram, ma szczyt, lub też w połowie odległości między największą i najmniejszą obserwacją, a σ jest w przybliżeniu równe jednej szóstej różnicy między największą i najmniejszą obswerwacją - co wynika właśnie z reguły trzech sigm.
Jednym z matematyków, których badania przyczyniły się do poznania własności rozkładu normalnego, był Carl Friedrich Gauss (1777-1855). Jako ciekawostkę warto wspomnieć, że na banknocie o nominale 10 niemieckich marek (będącym w obiegu do wprowadzenia euro w 2002 roku) wraz z podobizną Gaussa widniał wykres gęstości rozkładu normalnego.

Na koniec przykład ilustrujący zastosowanie rozkładu normalnego do opisu zjawisk ze świata przyrody, nawiązujący do rozważań z początku tego miniwykładu.
Przykład 3. Zakładając, że
a) wzrost kobiety jest zmienną losową o rozkładzie N(165,6) [cm],
b) wzrost mężczyzny jest zmienną losową o rozkładzie N(180,6) [cm],
oblicz prawdopodobieństwo, że wzrost przedstawiciela danej płci mieści się w przedziale [160 cm,180 cm].
Rozwiązanie.
a) Niech K~N(165,6). Wówczas
[tex]P(160\leq K\leq 180)=P\left(\frac{160-165}{6}\leq \frac{K-165}{6}\leq \frac{180-165}{6}\right)=P\left(-\frac{5}{6}\leq \frac{K-165}{6}\leq \frac{15}{6}\right)=[/tex]
[tex]=\Phi\left(\frac{15}{6}\right)-\Phi\left(-\frac{5}{6}\right)=\Phi\left(\frac{15}{6}\right)-\left(1-\Phi\left(\frac{5}{6}\right)\right)=\Phi\left(\frac{15}{6}\right)+\Phi\left(\frac{5}{6}\right)-1\approx[/tex]
[tex]\approx \Phi(2,5)+\Phi(0,83)-1=0,99379+0,79767-1=0,79146.[/tex]
b) Niech M~N(180,6). Wówczas
[tex]P(160\leq M\leq 180)=P\left(\frac{160-180}{6}\leq \frac{K-180}{6}\leq \frac{180-180}{6}\right)=P\left(-\frac{20}{6}\leq \frac{K-180}{6}\leq 0\right)=[/tex]
[tex]=\Phi\left(0\right)-\Phi\left(-\frac{20}{6}\right)=\Phi\left(0\right)-\left(1-\Phi\left(\frac{20}{6}\right)\right)=\Phi\left(0\right)+\Phi\left(\frac{20}{6}\right)-1\approx[/tex]
[tex]\approx \Phi(0)+\Phi(3,33)-1=0,50000+0,99957-1=0,49957.[/tex]
Zad. 1. Zebrano pewne dane pochodzące z dwóch rozkładów normalnych: N(μA,σA) i N(μB,σB). Na podstawie histogramów oceń, czy μA>μB, czy też μA<μB, oraz czy σA>σB, czy też może σA<σB. Zwróć uwagę na to, że skale na osiach obu histogramów są różne.

Zad. 2. Niech X~N(1,1). Oblicz:
a) P(X < -1);
b) P(|X| > 1).
Jako rozwiązanie podaj jedynie wynik.
Zad. 3. Według informacji podanych przez Ministerstwo Edukacji Narodowej (str. 7) w 2015 roku średni wynik na egzaminie gimnazjalnym z zakresu matematyki w części matematyczno-przyrodniczej wynosił 48% przy odchyleniu standardowym 23%. Zakładając, że rozkład wyników był normalny z takimi właśnie parametrami, oblicz prawdopodobieństwo, że uczeń w tej części zdobył więcej niż 70% punktów.
Uwaga. W rzeczywistości rozkład ten odbiegał nieco od rozkładu normalnego (por. wykres D w przytoczonym dokumencie).
Zad. 1. Uzasadnij, że gęstość rozkładu N(μ,1) można otrzymać poprzez przesunięcie gęstości rozkładu N(0,1) o odpowiedni wektor.
Zad. 2. Wiedząc, że X~N(2,4) i Y~N(3,6) i że te zmienne losowe są niezależne, oblicz P(|X+Y|<4). Jako rozwiązanie podaj jedynie wynik.
Zad. 3. Tak przedstawiał się rozkład wyników matury na poziomie podstawowym z języka polskiego i z matematyki w ostatnich latach:
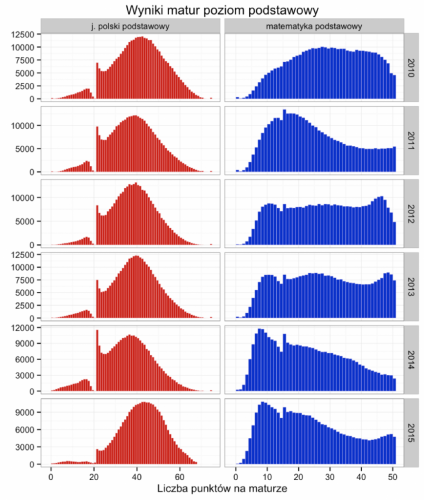
(wykres pochodzi ze strony http://smarterpoland.pl/index.php/2015/09/wyniki-z-matur-z-2015/). Spójrzmy na rozkład wyników z języka polskiego w 2015 roku. Wykazuje on podobieństwo do rozkładu normalnego poza pewną anomalią w okolicy 21 punktów (tj. 30% możliwej do zdobycia liczby punktów wynoszącej 70). Zaniedbując wspomnianą anomalię i biorąc pod uwagę tylko regularny fragment histogramu (ten tworzący kształt dzwonu), rozsądnym wydaje się założenie, że wyniki matury dają się opisać za pomocą rozkładu normalnego. W oparciu o histogram postaraj się oszacować parametry tego rozkładu (na podstawie tego, gdzie dzwon ma szczyt oraz na podstawie reguły trzech sigm), a następnie oblicz prawdopodobieństwo, że przy poczynionych założeniach maturzysta uzyskał co najmniej 50 punktów.
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Suma |
| Joanna Lisiowska | 1 | 0,5 | 1 | 2,5 |
| Adam Stachelek | 1 | 1 | 1 | 3 |
Klasyfikacja generalna:
Adam Stachelek (Szkoła Podstawowa nr 301 w Warszawie) - 18,5 punktu
Joanna Lisiowska (Katolicki Zespół Edukacyjny im. Piotr Skargi w Warszawie) - 17,5 punktu
Jakub Ptak (Szkoła Podstawowa nr 64 we Wrocławiu) - 5 punktów
Dawid Konieczko (Społeczne Gimnazjum z Oddziałami Dwujęzycznymi w Szprotawie) - 0 punktów
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Suma |
| Daria Bumażnik | 0,5 | 1 | 0,5 | 2 |
| Tomasz Stempniak | 1 | 1 | 1 | 3 |
Klasyfikacja generalna:
Tomasz Stempniak (I Liceum Ogólnokształcące w Ostrowie Wielkopolskim ) - 22,5 punktu
Daria Bumażnik (II Liceum Ogólnokształcące im. C. K. Norwida w Jeleniej Górze) - 18,5 punktu
Witold Barcz (Zespół Szkół Elektryczno-Mechanicznych w Nowym Sączu) - 1 punkt
Zad. 1. μA<μB, σA>σB.
Zad. 2.
a) [tex]P(X<-1)=P(X-1<-1-1)=P(X-1<-2)[/tex]
Skoro [tex]X\sim N(1,1)[/tex], to [tex]X-1\sim N(0,1)[/tex], a zatem
[tex]P(X<-1)=P(X-1<-2)=\Phi(-2)=1-\Phi(2)=[/tex]
[tex]=1-0,97725=0,02275.[/tex]
W końcowej części rachunków wykorzystaliśmy tożsamość: Φ(-x) = 1-Φ(x).
Wynik możemy otrzymać przy użyciu arkusza za pomocą formuły ROZKŁAD.NORMALNY(-1;1;1) lub ROZKŁAD.NORMALNY(-1-1;0;1) lub ROZKŁAD.NORMALNY.S(-1-1) (lub jeszcze kilku innych wariantów).
b) [tex]P(|X|>1)=P(X>1 \textrm{lub} X<-1)= P(X>1)+P(X<-1)[/tex]
Drugi składnik został już obliczony w punkcie a).
[tex]P(X>1)=P(X-1>1-1)=P(X-1<0)[/tex]
Skoro [tex]X\sim N(1,1)[/tex], to [tex]X-1\sim N(0,1)[/tex], a zatem
[tex]P(X>1)=P(X-1>0)=1-\Phi(0)=1-0,50000=0,50000.[/tex]
Pierwszy składnik można obliczyć przy użyciu komputera na wiele sposobów, np. 1-ROZKŁAD.NORMALNY(1;1;1), 1-ROZKŁAD.NORMALNY(1-1;0;1), 1-ROZKŁAD.NORMALNY.S(0)... Warto jednak zwrócić uwagę, że rozkład normalny N(μ,σ) jest symetryczny względem μ, a zatem prawdopodobieństwo, że zmienna losowa o rozkładzie N(1,1) jest większa od 1, wynosi ½ (do obliczenia czego nie potrzebne są tablice dystrybuanty rozkładu normalnego ani komputer).
Ostatecznie:
[tex]P(|X|>1)=0,50000+0,02275=0,52275.[/tex]
Zad. 3. Niech zmienna losowa X oznacza, jaką część liczby punktów możliwej do zdobycia na egzaminie gimnazjalnym z zakresu matematyki w części matematyczno-przyrodniczej zdobył uczeń. Zakładamy, że X~N(0,48 , 0,23). W takim razie
[tex]P(X>0,7)=P\left(\frac{X-0,48}{0,23}>\frac{0,7-0,48}{0,23}\right)=[/tex]
[tex]=P\left(\frac{X-0,48}{0,23}>\frac{0,7-0,48}{0,23}\right)\approx P\left(\frac{X-0,48}{0,23}>0,96\right).[/tex]
Skoro [tex]X\sim N(0,48 , 0,23)[/tex], to [tex]\frac{X-0,48}{0,23}\sim N(0,1)[/tex], a zatem
[tex]P(X>0,7)=P\left(\frac{X-0,48}{0,23}>0,96\right)=1-\Phi(0,96)=0,16852.[/tex]
Warto zwrócić uwagę, że w tym zadaniu zastosowaliśmy dwa uproszczenia. Pierwsze polega na tym, że wyniki egzaminu gimnazjalnego są podawane z dokładnością do całkowitych części procentu, a zatem nie jest możliwe uzyskanie jako wyniku każdej liczby z przedziału [0,1], podczas gdy rozkład normalny jako rozkład ciągły ma to do siebie, że zmienna losowa o tym rozkładzie może przyjmować każdą wartość. Drugie uproszczenie polega na tym, ze zmienna losowa o rozkładzie normalnym może przyjąć jako wartość każdą liczbę rzeczywistą, chociaż wynik egzaminu nie może być ujemny i nie może przekroczyć 100%. Uproszczenia poczynione w tym zadaniu są standardowymi założeniami, jakie często Czyni się, posługując się rozkładem normalnym w rachunkach dotyczących zjawisk w otaczającym nas świecie.
Zad. 1. Pamiętamy, że jeśli przesuniemy wykres funkcji o wzorze y = f(x) o wetkor o współrzędnych [p,q], to otrzymamy wykres funkcji o wzorze y = f(x-p)+q. Gęstość rozkładu N(0,1) jest zadana wzorem:
[tex]f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}.[/tex]
Jeśli przesuniemy ten wykres o wektor o współrzędnych [μ,0], to otrzymamy wykres funkcji zadanej wzorem:
[tex]f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2}},[/tex]
która jest gęstością rozkładu N(μ,1).
Zad. 2. Skoro X~N(2,4), Y~N(3,6) i te zmienne losowe są niezależne, to X+Y~N(2+3, √42+62) = N(5,√52) = N(5,2√13). Dla wygody przyjmijmy oznaczenie: Z = X+Y.
[tex]P(|Z|<4)=P(-4<Z<4)=P\left(\frac{-4-5}{2\sqrt{13}}<\frac{Z-5}{2\sqrt{13}}<\frac{4-5}{2\sqrt{13}}\right)=[/tex]
[tex]=P\left(\frac{-9\sqrt{13}}{26}<\frac{Z-5}{2\sqrt{13}}<\frac{-\sqrt{13}}{26}\right)[/tex]
Skoro [tex]X\sim N(3, 2\sqrt{13})[/tex], to [tex]\frac{Z-5}{2\sqrt{13}}\sim N(0,1)[/tex]. wobec tego
[tex]P(|Z|<4)=P\left(\frac{-9\sqrt{13}}{26}<\frac{Z-5}{2\sqrt{13}}<\frac{-\sqrt{13}}{26}\right)=\Phi\left(\frac{-\sqrt{13}}{26}\right)-\Phi\left(\frac{-9\sqrt{13}}{26}\right)\approx [/tex]
[tex]\approx \Phi(-0,14)-\Phi(-1,25)=(1-\Phi(0,14))-(1-\Phi(1,25))=[/tex]
[tex]=1-\Phi(0,14)-1+\Phi(1,25)=\Phi(1,25)-\Phi(0,14)=[/tex]
[tex]=0,89435-0,55567=0,33868.[/tex]
W końcowej części rachunku dwukrotnie posłużyliśmy się tożsamością Φ(-x) = 1-Φ(x).
Dokonując obliczeń na arkuszu kalkulacyjnym, może podać wynik bez dokonywania powyższych przekształceń, opierając się jedynie na tym, że Z~N(5,2√13). Wówczas możemy posłużyć się formułą ROZKŁAD.NORMALNY(4;2;2*PIERWIASTEK(13))-ROZKŁAD.NORMALNY(-4;2;2*PIERWIASTEK(13)).
Zad. 3. Oglądając wykres, można odnieść wrażenie, że maksimum jest osiągnięte przy 45 punktach. Przyglądając się prawej, bardziej regularnej części wykresu, widzimy, że dane sięgają aż do 70 punktów, a zatem prawa połowa dzwonu jest rozpięta nad osią OX na odcinku o długości 70-45 = 25. Jednocześnie gdybyśmy popatrzyli na lewą część wykresu i pominęli w wyobraźni anomalię w okolicy 21 punktów, to zauważylibyśmy, że dzwon sięgałby mniej więcej do 20 punktów, za zatem także jego lewa połowa byłaby rozpięta nad osią OX na odcinku o długości 45-20 = 25. Skoro 25/3 ≈ 8, to przyjmujemy, że wynik z matury z języka polskiego na poziomie rozszerzonym można modelować za pomocą zmiennej losowej X o rozkładzie N(45,8).
Oczywiście zadanie polega na szacowaniu "na oko", a zatem możliwe są też inne choć zbliżone wyniki. "Odgadywanie" parametrów rozkładów na podstawie obserwowanych danych nazywa się w statystyce estymacją i zazwyczaj dokonuje się go w sposób bardziej wyrafinowany niż poprzez oglądanie wykresu. Szerzej o estymacji w ramach ligi zadań z analizy danych w przyszłym roku szkolnym.
W tym miejscu warto uczynić taką uwagę, jaka została uczyniona przy zadaniu 3 dla gimnazjalistów. Oprócz zaniedbania pewnej nieregularności w okolicy 21 punktów w tym zadaniu zastosowaliśmy jeszcze dwa inne uproszczenia. Pierwsze polega na tym, że wyniki matury są wyznaczanie z dokładnością do pełnych punktów, a zatem nie jest możliwe uzyskanie jako wyniku każdej liczby z przedziału [0,70], podczas gdy rozkład normalny jako rozkład ciągły ma to do siebie, że zmienna losowa o tym rozkładzie może przyjmować każdą wartość (także ułamkową). Drugie uproszczenie polega na tym, ze zmienna losowa o rozkładzie normalnym może przyjąć jako wartość każdą liczbę rzeczywistą, chociaż wynik egzaminu nie może być ujemny i nie może przekroczyć 70 punktów. Uproszczenia te są standardowymi założeniami, jakie często czyni się, posługując się rozkładem normalnym w rachunkach dotyczących zjawisk w otaczającym nas świecie.
Skoro zakładamy, że X~N(45,8), to
[tex]P(X\geq 50)=P\left(\frac{X-45}{8}\geq \frac{50-45}{8}\right)=P\left(\frac{X-45}{8}\geq 0,625\right).[/tex]
Zmienna losowa [tex]\frac{X-45}{8}[/tex] ma w tym wypadku rozkład N(0,1), a zatem
[tex]P(X\geq 50)=P\left(\frac{X-45}{8}\geq 0,625\right)=1-\Phi(0,625)=1-0,73565=[/tex]
[tex]=0.26435.[/tex]
Wynik możemy otrzymać przy użyciu arkusza za pomocą jednej z poniższych formuł: 1-ROZKŁAD.NORMALNY(50;45;8) lub ROZKŁAD.NORMALNY((50-45)/8;0;1) lub ROZKŁAD.NORMALNY.S((50-45)/8).




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
