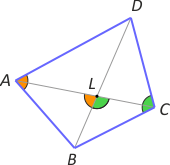
Zad. 1. W czworokącie wypukłym ABCD zachodzi |AB|=|BC|. Na przekątnej BD obrano punkt K, taki że suma miar kątów AKB i BKC jest równa sumie miar kątów A i C. Wykaż, że |AK|·|CD| = |KC|·|AD|.
Zad. 2. Stosunek długości boków trójkąta wynosi 3:4:6. Niech K, L i M oznaczają spodki dwusiecznych kątów. Oblicz stosunek pola wyjściowego trójkąta do pola trójkąta KLM.
Zad. 3.W trójkącie o bokach długości: |AB|=√3, |BC|=4 i |AC|=√7 poprowadzono środkową BD. Okręgi wpisane w trójkąty ABD i BDC są styczne do BD odpowiednio w punktach M i N. Oblicz długość MN.
Zad. 4. (wolna amerykanka) W trójkącie ostrokątnym ABC dane są miary kątów α, β i γ. Znajdź stosunek, w jakim ortocentrum (punkt przecięcia prostych zawierających wysokości) dzieli wysokość opuszczoną z wierzchołka A.
Za zadania 1-3 punkty zdobyli:
30 pkt. - Michel Migas (student, PW) oraz Tadeusz Porzucek (emerytowany nauczyciel, Gostyń)
10 pkt. - Jacek Bagiński (nauczyciel matematyki, I LO Kraków),
Za zadanie 4 (wolna amerykanka) 10 pkt. zdobyli : J. Bagiński, M. Migas, T. Porzucek oraz Zygmunt Krawczyk (nauczyciel, SLO Żary). Gratulujemy!
Zad. 1. Obierzmy na przekątnej BD punkt L taki, że |∡ALB| = |∡BAD|. Zauważmy, że trójkąty ABL i ABD są podobne, bo dodatkowo mają wspólny kąt ABD. Stąd otrzymujemy proporcję |BL|:|AB| = |AB|:|BD|, czyli |BL|·|BD| = |AB|2. Podstawiając BC w miejsce AB, otrzymujemy |BL|·|BD| = |BC|2, a następnie proporcję |BL|:|BC| = |BC|:|BD|, z której wynika podobieństwo trójkątów BLC i BCD, a z niego przystawanie kątów BLC i BCD. Oznacza to, że punkt L pokrywa się z K. Z obu podobieństw otrzymujemy kolejne proporcje: |AL|:|AB| = |AD|:|BD| oraz |BC|:|CL| = |BD|:|DC|. Mnożąc je stronami i uwzględniając założenie |AB| = |BC|, otrzymujemy |AL|:|CL| = |AD|:|DC|, skąd wynika teza.
Zad. 2. Zachodzi PABC : PKLM = PABC : (PABC – PALM – PMBK – PKCL) = 1 : (1 – PALM/PABC – PMBK/PABC – PKCL/PABC) = 1 : (1 – |AL|·|AM|/|AC|·|AB| – |MB|·|BK|/|AB|·|BC| – |KC|·|CL|/|BC|·|CA|). Długości poszczególnych odcinków obliczamy, korzystając z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta. Przykładowo zauważmy, że |AL|:|LC| = |AB|:|BC|, skąd otrzymujemy |AL| = 6a·3a/(6a+4a). Ostatecznie szukany stosunek pól wynosi 35/8.
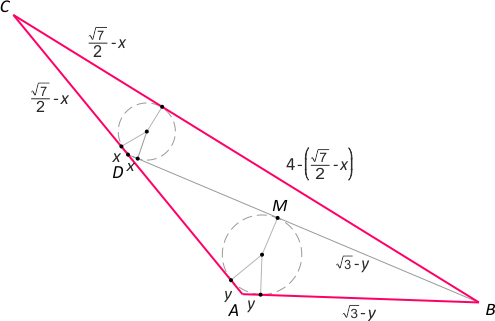
Zad. 3. Wprowadźmy oznaczenia jak na poniższym rysunku. Wystarczy rozwiązać układ równań: |MN|+x = √7/2–y oraz |MN|+√3–y = 4–(√7/2–x). W wyniku otrzymamy |MN| = 2–√3/2.
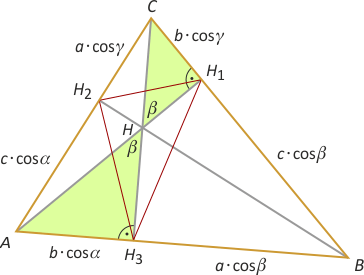
Zad. 4. (wolna amerykanka) Rozważmy trójkąt spodkowy H1H2H3. Odcina on od wyjściowego trójkąty do niego podobne w skali równej kosinusowi kąta przy odpowiednim wierzchołku (patrz rozwiązanie zadania 4 z grudnia 2017). Korzystając z tego faktu, obliczamy długości poszczególnych odcinków. W trójkącie AH3H mamy sinβ = bcosα/|AH| skąd |AH| = bcosα/sinβ. W trójkącie CHH1 mamy |HH1| = bcosα/tgβ. Dzieląc te zależności stronami, otrzymujemy |AH|:|HH1| = cosα:(cosβ·cosγ).
