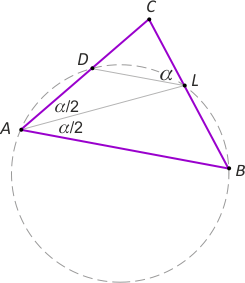
Zad. 1. Niech AL będzie dwusieczną w trójkącie ABC, a punkt D leży na boku AC tak, że kąty DLC i BAC są przystające. Wykaż, że |DL| = |LB|.
Zad. 2. W trapezie podstawy mają długość 10 i 26, a przekątne są prostopadłe do ramion. Oblicz pole tego trapezu.
Zad. 3. Czworokąt ABCD o prostopadłych przekątnych wpisano w okrąg. Z wierzchołków B i C poprowadzono proste prostopadłe do boku AD. Przecinają one przekątne AC i BD odpowiednio w punktach E i F. Oblicz długość EF, wiedząc że |BC| = 1.
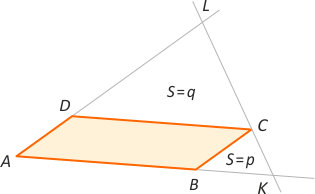
Zad. 4. (wolna amerykanka) W równoległoboku ABCD prosta przechodząca przez wierzchołek C przecina proste AB i AD w punktach K i L. Pola trójkątów KBC i CDL wynoszą odpowiednio p i q. Znajdź pole równoległoboku ABCD.
Za zadania 1-3 punkty 30 punktów zdobyli: Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Michel Migas (student PW) oraz Tadeusz Porzucek (emerytowany nauczyciel, Gostyń). Za zadanie 4 (wolna amerykanka)10 punktów zdobyli: J. Bagiński, M. Migas, T. Porzucek oraz Zygmunt Krawczyk (nauczyciel, SLO Żary). Gratulujemy!
Zad. 1. Zauważmy, że suma miar kątów DAB i BLD wynosi 180°, a stąd na czworokącie ABLD
można opisać okrąg. Na cięciwach DL i LB oparte są kąty przystające, więc te cięciwy mają równą długość.
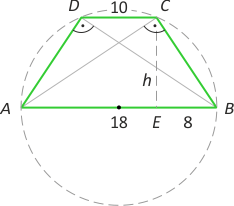
Zad. 2. Z danych wynika, że trapez jest równoramienny i wpisany w okrąg o średnicy AB. Z własności wysokości opuszczonej na przeciwprostokątną w trójkącie prostokątnym mamy h = √(18·8) = 12. Stąd pole trapezu wynosi 216.
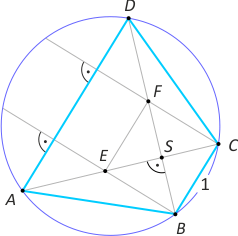
Zad. 3. Zauważmy, że E jest ortocentrum trójkąta ABD, a F - trójkąta ACD. Łatwo wykazać, że obraz ortocentrum w symetrii względem boku leży na okręgu opisanym na trójkącie. Z tej własności wynika, że punkty E i C oraz F i B są symetryczne względem S, co wobec prostopadłości odcinków EC i FB oznacza, że czworokąt EBCF jest rombem. Stąd |EF| = 1.
Zad. 4. Oznaczmy przez S pole trójkąta AKL. Wówczas szukane pole równoległoboku wynosi S–p–q. Zauważmy, że trójkąty AKL, DCL i BCK są podobne, przy czym |DL|:|AD| = |DL|:|BC| = √(q/p), skąd |AL| = |AD|(1 + √(q/p)). Dalej mamy |AL|:|DL| = √(S/q) = |AD|/|DL| · (1+√(q/p)) = √(p/q)·(1+√(q/p)). Stąd po przekształceniach mamy S = p+q+2√(pq). Ostatecznie szukane pole wynosi 2√(pq).
