Kompresja - to transformacja oryginalnej reprezentacji danych w inną reprezentację o mniejszej liczbie bitów.
Wyróżniamy dwa główne rodzaje kompresji:
a) stratną - w wyniku kompresji pogarsza się jakość w stosunku do oryginału,
b) bezstratną - w wyniku kompresji jakość jest zachowana względem oryginału.
Przykład
Rozważmy następujący początkowy ciąg bajtów opisujący obrazek:
5 3 3 3 6 6 6 6 5 5 5 5 1 1 1 1 3 2 2 2 7 7 7 7 8
Zastąpmy w początkowym ciągu identyczne bajty wskaźnikiem opisującym, ile bajtów danego koloru zastapiono, np. 6|4 oznacza, że kolor 6 występuje w czterech sąsiednich bajtach. Otrzymamy kompresję bezstratną:
5 3|3 6|4 5|4 1|4 3 2|3 7|4 8
W wyniku dekompresji tego zapisu zostanie odtworzony początkowy ciąg bajtów.
Zastąpmy w początkowym ciągu kolory sasiednie różniące się o 1 przez mniejszą z ich wartości, np. jeśli sąsiednie są kolory 6 i 5, to wszystkie 6 zastąpimy przez 5. Następnie poddajemy nowy ciąg poprzednio opisanej kompresji. Otrzymamy kompresję stratną:
5 3|3 5|8 1|4 2|4 7|5
W wyniku dekompresji tego zapisu początkowy ciąg bajtów nie zostanie odtworzony dokładnie. Otrzymamy:
5 3 3 3 5 5 5 5 5 5 5 5 1 1 1 1 2 2 2 2 7 7 7 7 7
Oszczędność kompresji - zakładając, że na każdą z liczb w zapisie potrzebujemy x bitów/bajtów, to
- ciąg oryginalny zajmuje 25*x bit/B,
- kompresja bezstratna zajmuje 15*x bit/B, zatem oszczędność wynosi 10*x bit/B,
- kompresja stratna zajmuje 11*x bit/B, zatem oszczędność wynosi 14*x bit/B.
Zad. 1. Jaki rodzaj kompresji reprezentują podane sposoby kompresji danych? Dlaczego są one właściwe (tzn. z czego wynika wybór takiego rodzaju kompresji)?
a) MP3
b) JPEG
Zad. 2. Pewien kwadratowy obrazek po skompresowaniu algorytmem ByteRun jest opisany ciągiem wartości: 2,1,1,2,-3,1,-2,2,-2,1,-2,2,-3,1,0,3,-4,1,0,3,-2,1,-5,4. Odtwórz ten obrazek oraz oblicz, ile wyniosła oszczędność zastosowanej kompresji. Przedstaw obliczenia a obrazek załącz w pliku graficznym.
Zad. 3. Za pomocą kodowania Huffmana zakoduj poniższe wyrażenia oraz podaj (z obliczeniami) najmniejszą oszczędność danych wynikającą z tego kodowania.
a) matematyka
b) twierdzenie Tarskiego o ultrafiltrze
W przedostatniej już rozgrywce tej edycji zdobycz punktowa prezentuje się następująco:
- 3,25 pkt. - Andrzej Piasecki - administrator IT z Oleśnicy,
- 2,75 pkt. - Krystyna Lisiowska - redaktor z Warszawy.
Po ośmiu miesiącach trwania Ligi czołówka prezentuje się nastęująco:
- 23,25 pkt. - Andrzej Piasecki
- 20,75 pkt. - Krystyna Lisiowska
- 14,25 pkt. - Tomasz Tomiczek
- 9 pkt. - Krzysztof Danielak
- 3 pkt. - Michał Żłobicki
Zad. 1. Oba sposoby kompresji należą do kompresji stratnej. W standardzie MP3 wykorzystuje się specyficzne właściwości ludzkiego słuchu. Polega on na usunięciu tych informacji z dźwięku, które są niezauważalne lub mało istotne dla słuchu człowieka. W przypadku standardu JPEG wykorzystano fakt, że nasz wzrok jest bardziej wrażliwy na nieznaczne różnice w jasności niż w barwie. Dlatego redukcji może ulec informacja o zmianach barwy poszczególnych pikseli.
Zad. 2. Po dekompresji otrzymamy obrazek o wymiarach 6x6 = 36 [j.]. Po dekompresji mamy zapis długości 24 [j.], zatem oszczędność wynosi 12 [j.], czyli 1/3 pierwotnego rozmiaru. Po odtworzeniu i pokolorowaniu obrazku, otrzumamy:
Zad. 3. Rozwiązanie:
a) matematyka - przykładowe drzewo: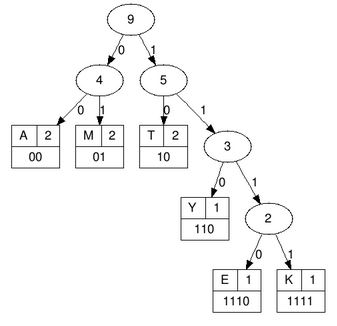
Oszczędność:
* 6 różnych znaków możemy zapisać na 3 bitach, zatem 10*3 = 30 bitów,
* po zakodowaniu mamy 0100101110010010110111100 => 25 bitów,
* 30 - 25 = 5.
b) twierdzenie Tarskiego o ultrafiltrze - przykładowe drzewo: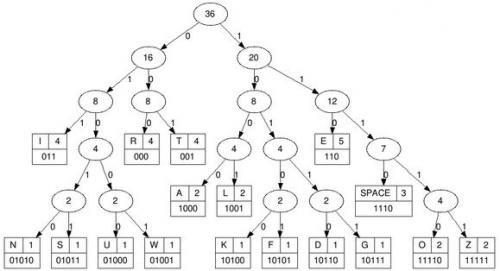
Oszczędność:
* 17 różnych znaków możemy zapisać na 5 bitach, zatem 36*5 = 180 bitów,
*
po zakodowaniu mamy 001010010111100001011011111110010100111101110
0011000000010111010001111010111111101110111101110010001001001000
100010101011100100100011111110 => 139 bitów,
* 180 - 139 = 41 bitów.
Widzimy, że wraz ze wzrostem długości kodowanej wiadomości wzrasta oszczędność.
To
rozwiązanie nie uwzględnia przesłania struktury drzewa do odkodowania
wiadomości, na którą musimy poświęcić po bicie na każdy węzeł i liść
oraz minimalną długość na każdy z różnych znaków:
a) matematyka 11+6*3 = 29 bitów,
b) twierdzenie Tarskiego o ultrafiltrze: 33+17*5 = 118 bitów.
Za uwzględnienie długości drzewa do przesłania zadnie będzie premiowane +0,5pkt.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
