Zad. 1. Jaką resztę daje przy dzieleniu przez 5 liczba 9876543212019?
Zad. 2. W okrąg o promieniu 6 cm wpisano trójkąt równoramienny, którego podstawa też ma 6 cm długości. Oblicz pole tego trójkąta.
Zad. 3. W trapezie równoramiennym długości podstaw są równe 9 cm i 3 cm, zaś ramię ma długość 5 cm. Oblicz odległości punktu przecięcia przekątnych tego trapezu od obu jego podstaw.
W maju punkty zdobyli:
• 3 pkt. – Michał Dźwigaj SP 1 Przemków, Joanna Galik SP 5 Wrocław, Anna Cichowska SP 14 Lubin, Aleksandra Strzelecka NSP Wilkowyja, Gabriela Brzoza G Dwujęzyczne Góra;
• 2,5 pkt. – Wiktoria Mróz SP Wyrzysk, Michał Plata SP 2 Syców, Wiktoria Jaguszczak SP Grębocice, Agata Lefler ZSS Wołów, Tomasz Lefler ZSS Wołów, Adam Chowanek SP Mieroszów, Hanna Laszkiewicz ZSK Jelenia Góra, Marta Sibielec G 48 Wrocław, Wojciech Domin SP Pisarzowice, Michał Węgrzyn SP 9 Wrocław, Wojciech Haładewicz SP 2 Siechnice, Wojciech Szwarczyński SP Kowalowa, Kacper Woszczek SP Mieroszów;
• 2 pkt. – Cezary Rębiś ZSO Jedlnia-Letnisko.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Ostatnią cyfrą dowolnej potęgi liczby zakończonej cyfrą 1 jest cyfra jeden. Zatem reszta z dzielenia liczby 9876543212019przez 5 jest liczba 1.
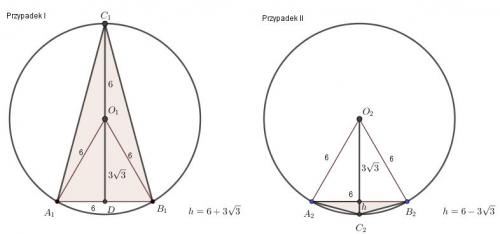
Zad.2. Rozpatrujemy dwa przypadki: Przypadek I. Trójkąt A1B1O1 jest trójkątem równobocznym o wysokości [tex] 3\sqrt{3}[/tex]. Trójkąt A1B1C1 jest trójkątem równoramiennym o podstawie 6 i wysokości [tex] 6 + 3\sqrt{3} [/tex]. Pole trójkąta A1B1 C1 wynosi [tex] 18+9\sqrt{3} [/tex]. Przypadek II. Trójkąt A2B2O2 jest trójkątem równobocznym o wysokości [tex] 3\sqrt{3} [/tex]. Trójkąt A1B1C1 jest trójkątem równoramiennym o podstawie 6 i wysokości [tex] 6 - 3\sqrt{3} [/tex]. Pole trójkąta A2B2C2 wynosi [tex] 18-9\sqrt{3} [/tex].
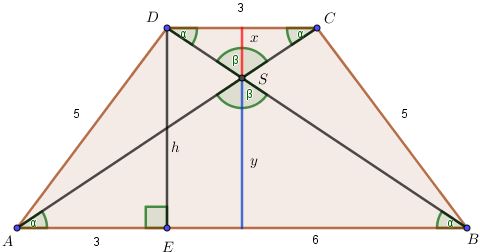
Zad. 3. Trójkąt AED jest prostokątny, stąd na podstawie twierdzenia Pitagorasa wysokość wynosi 4 cm. Trójkąty ABS i CDS są podobne na podstawie cechy KKK (kąty naprzemianległe i wierzchołkowe). Oznaczmy przez x i y odpowiednio odległości od krótszej i dłuższej podstawy, wówczas x + y = 4 i x/y = 3/9. Z otrzymanego układu równań otrzymujemy, że odległość punktu przecięcia od krótszej podstawy wynosi 1 cm a od dłuższej 3 cm.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
