Zad. 1. Michał wyszedł z domu, mając w kieszeni pewną liczbę złotówek i pięciozłotówek, razem kwotę większą od 140 zł, a mniejszą od 150 zł. Wydał trzecią część posiadanej gotówki. Po powrocie do domu stwierdził, że ma tyle złotówek, ile przedtem miał pięciozłotówek i tyle pięciozłotówek, ile przedtem miał złotówek. Jaką kwotą dysponował, wychodząc z domu?
Zad. 2. Jacek miał wziąć udział w obozie matematycznym, ale zachorował i zamiast niego na obóz pojechał jego brat, dwa razy od niego starszy. Ta zamiana spowodowała, że średnia wieku uczestników obozu wzrosła o rok. Oblicz, ile lat ma Jacek, jeżeli w obozie wzięło udział 12 osób.
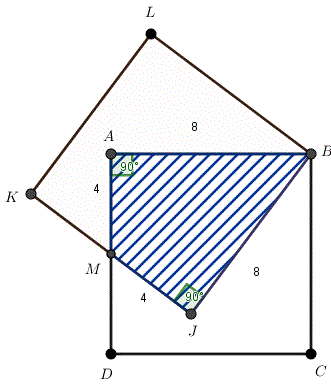
Zad. 3. ABCD i BJKL to kwadraty o boku długości 8 cm. Punkt M jest wspólnym środkiem odcinków AD i JK. Ile wynosi pole sześciokąta BCDMKL?
W czerwcu punkty zdobyli:
- 3 pkt. – Kacper Woszczek SP Mieroszów, Adam Chowanek SP Mieroszów, Marta Sibielec G 48 Wrocław, Michał Plata SP 2 Syców, Agata Lefler ZSS Wołów, Tomasz Lefler ZSS Wołów, Michał Węgrzyn SP 9 Wrocław, Wiktoria Mróz SP Wyrzysk, Wojciech Domin SP Pisarzowice, Wojciech Szwarczyński SP Kowalowa, Michał Dźwigaj SP 1 Przemków, Joanna Galik SP 5 Wrocław, Anna Cichowska SP 14 Lubin, Aleksandra Strzelecka NSP Wilkowyja, Gabriela Brzoza G Dwujęzyczne Góra i Hanna Laszkiewicz ZSK Jelenia Góra;
- 2 pkt. – Wiktoria Jaguszczak SP Grębocice, Wojciech Haładewicz SP 2 Siechnice, Kacper Przywara ZSO Józefów na Wisłą, Cezary Rębiś ZSO Jedlnia-Letnisko.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Po 9 miesiacach trwania ligi powyżej 20 pkt. (na 27 możliwych) zdobyli:
- 26 pkt: Hanna Laszkiewicz ZSK Jelenia Góra,
- 25,5 pkt: Gabriela Brzoza GM Dwujęzyczne Góra, Aleksandra Strzelecka NSP Wilkowyja,
- 24,5 pkt: Wiktoria Mróz SP Wyrzysk, Michał Plata SP 2 Syców,
- 24 pkt: Joanna Gaik SP 5 Wrocław, Agata i Tomasz Lefler ZSS Wołów, Marta Sibielec GM 48 Wrocław,
- 23,5 pkt: Michał Dźwigaj SP 1 Przemków, Michał Węgrzyn SP 9 Wrocław,
- 23 pkt: Agata Cichowska SP 14 Lubin, Wojciech Domin SP Pisarzowice,
- 20,5 pkt: Wojciech Haładewicz SP 2 Siechnice.
Laureatów Ligi popdajemy tutaj.
Zad. 1. Niech x – liczba złotówek, y – liczba pięciozłotówek w kieszeni Michała. Z treści zadania wiemy, że x+5y > 140 i x+5y < 150. Michał wydał [tex]\frac{1}{3}[/tex]posiadanej gotówki i obecnie ma tyle złotówek, ile przedtem miał pięciozłotówek i tyle pięciozłotówek, ile przedtem miał złotówek. Zatem teraz dysponuje kwotą 5x+y =[tex]\frac{2}{3}[/tex].(x+5y), skąd y =[tex]\frac{13}{7}[/tex]x. Po podstawieniu otrzymujemy nierówności x+5.[tex]\frac{13}{7}[/tex]x > 140 i x+5.[tex]\frac{13}{7}[/tex]x < 150, czyli x > 13[tex]\frac{11}{18}[/tex]i x < 14[tex]\frac{7}{12}[/tex]. Jedyną liczbą całkowitą w tym przedziale jest 14. Zatem x = 14 i y = 13/7.14 = 26. Michał wychodząc z domu miał 14 + 26 . 5 = 144 zł.
Zad. 2. Oznaczmy przez j wiek Jacka, a przez x - łączny wiek pozostałych uczestników obozu. Na podstawie treści zadania otrzymujemy równanie [tex]\frac{x+j}{12}=\frac{x+2j}{12}-1[/tex], skąd x = 12.
Zad. 3. Zakreskowany deltoid jest częścią wspólną kwadratów. Jego pole wynosi 32 cm2. Pole sześciokąta BCDMKL wynosi 2 . 64 – 32 = 96 cm2.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
