Zad. 1. Pewna liczba naturalna ma 4 dzielniki, których średnia arytmetyczna jest równa 10. Znajdź wszystkie takie liczby.
Zad. 2. Wyznacz długości boków trójkątów prostokątnych, których obwód jest równy polu trójkąta.
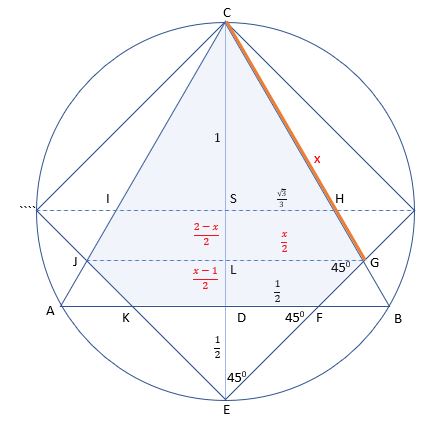
Zad. 3. W okrąg o promieniu 1 wpisano kwadrat i trójkąt równoboczny o wspólnym wierzchołku. Oblicz pole części wspólnej tych figur.
W maju punkty zdobyli:
- 3 pkt. – Kasper Radom II LO Lubin, Laura Stefanowska Katolickie LO Legnica, Szymon Misiewicz CKZiU Strzelin, Joanna Lisiowska XXI LO Warszawa;
- 2,5 pkt. – Julia Musiał II LO Tczew, Piotr Zug LO Olesno;
- 2 pkt. – Marcin Wiśniewski LO Ząbkowice Śląskie i Alex Kalinowski LO Góra
- 1 pkt. – Wiktoria Malinowska XXVII LO Warszawa.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Oznaczmy szukaną liczbę przez n. Liczba ta ma 4 dzielniki 1, p, q, n. Iloczyn p . q też jest dzielnikiem liczby n, więc p . q = n i p, q są liczbami pierwszymi lub p . q = n i q = p2 i p jest liczbą pierwszą, w przeciwnym wypadku liczba n miałaby więcej dzielników. Średnia dzielników tej liczby wynosi 10, zatem ich suma wynosi 40. Pozostaje sprawdzić kilka możliwości: {1, 3, 5, 15}, {1, 3, 7, 21}, {1, 2, 4, 8}, {1, 3, 9, 27}. W pozostałych przypadkach suma liczb jest większa niż 40. Warunki zadania spełnia tylko liczba 27.
Zad. 2. W każdy trójkąt można wpisać okrąg. Pole trójkąta opisanego na okręgu o promieniu r wyraza się wzorem [tex] P = \frac{1}{2} r (a + b + c) [/tex]. Z treści zadania [tex] a + b + c = \frac{1}{2} r (a + b + c) [/tex] a stąd r = 2. Warunki zadania spełniają, więc trójkąty prostokątne opisane na okręgu o promieniu 2. Wyznaczymy boki takich trójkątów w zależności od a. Przeciwprostokątna wynosi c = a + b – 4. Pole trójkąta jest równe obwodowi, zatem [tex] \frac{ab}{2}=2a + 2b-4 [/tex], skąd [tex] b=\frac{4a-8}{a-4} [/tex], [tex] c=\frac{a^2-4a+8}{a-4} [/tex], dla a >4.
Zad. 3. Pole zacieniowanej figury składa się z pola trójkąta równobocznego JGC i trapezu KFGJ. Promień okręgu opisanego na trójkącie równobocznym o boku a wynosi [tex]R=\frac{2}{3}h[/tex], czyli [tex]1=\frac{2}{3}h[/tex], stąd [tex]h=\frac{3}{2} [/tex]. Ze wzoru na wysokość trójkąta równobocznego obliczamy bok trójkąta [tex]a =\sqrt{3}[/tex]. R = CS = 1, SD = 1,5 - 1 = [tex] \frac{1}{2} [/tex], stąd [tex]DE=1-\frac{1}{2}=\frac{1}{2}[/tex] oraz [tex] KF=1 [/tex], [tex] SH=\frac{2}{3} \cdot\frac{1}{2}\sqrt{3}=\frac{\sqrt{3}}{3} [/tex]. Niech [tex] CG=x [/tex], stąd [tex]LG=\frac{x}{2}[/tex] oraz [tex] LE=\frac{x}{2}[/tex], bo trójkat GLE jest prostokątny równoramienny, więc [tex] LD=LE-DE=\frac{x-1}{2}[/tex] oraz [tex]LS=SE-LE=\frac{2-x}{2} [/tex]. Na podstawie podobieństwa trójkątów SHC i CLG otrzymujemy proporcję [tex] \frac{SH}{CS}=\frac{GL}{CL} [/tex], czyli [tex] \frac{\frac{\sqrt{3}}{3}}{1}=\frac{\frac{x}{2}}{1+\frac{2-x}{2}} [/tex], stąd [tex] x=2\sqrt{3}-2 [/tex]. Pole figury zacieniowanej składa się zatem z trójkąta równobocznego o boku [tex] 2\sqrt{3}-2 [/tex] oraz trapezu o podstawach 1 i [tex] 2\sqrt{3}-2 [/tex] oraz wysokości [tex] \frac{2\sqrt{3}-3}{2} [/tex], czyli PCJKFG = PCJG + PJKFG = [tex] \frac{(2\sqrt{3}-2)^2\sqrt{3}}{4}+\frac{(2\sqrt{3}-2+1)\frac{2\sqrt{3}-3}{2}}{2}=\frac{8\sqrt{3}-9}{4} [/tex].
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
