Zad. 1. Jaką długość ma bok trójkąta równobocznego, którego pole jest równe polu figury F = {(x, y): x ∈ <-3, 3> i [x] = [y2] i y ∈ R}.
Zad. 2. Danych jest 5 odcinków o długościach odpowiednio 1, 3, 5, 7, 9 jednostek. Oblicz prawdopodobieństwo, że trzy losowo wybrane różne odcinki są wysokościami pewnego trójkąta.
Zad. 3. W trójkąt ABC o obwodzie 4 wpisano okrąg i poprowadzono styczną do okręgu równoległą do boku AB. Styczna przecięła boki trójkąta odpowiednio w punktach D i E. Jaką największą długość może mieć odcinek DE?
W czerwcu punkty zdobyli:
• 3 pkt. – Marcin Wiśniewski LO Ząbkowice Śląskie, Piotr Zug LO Olesno, Laura Stefanowska Katolickie LO Legnica, Joanna Lisiowska XXI LO Warszawa, Alex Kalinowski LO Góra;
• 2,5 pkt. – Julia Musiał II LO Tczew;
• 1 pkt. – Szymon Misiewicz CKZiU Strzelin.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Pole figury F zakreskowane poniżej wynosi [tex]2\sqrt{3}[/tex]. Pole trójkata równobocznego o boku a jest równe [tex]\frac{a^2\sqrt{3}}{4}[/tex], więc [tex]a=2\sqrt{2}[/tex].
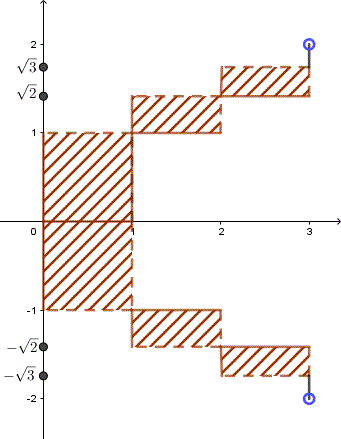
Zad. 2. Zdarzenie elemntarne polega na wylosowaniu spośród pięciu odcinkow o długościach 1, 3, 5, 7 i 9 jednostek trzech różnych odcinków. Zakładamy, że wszystkie zdarzenia elementarne są jednakowo prawdopodobne. Przestrzeń zdarzeń elementarnych Ω jest zbiorem wszystkich trzyelementowych pozdzbiorów zbioru 5-elementowego, A - zdarzenie polegające na wylosowaniu takich odcinków, które są wysokościami pewnego trókąta. Jeżeli wylosowano odcinki o dugościach ha, hb, hc (wysokości opuszczone odpowiednio na boki a, b, c), ha<hb<hc i ha, hb, hc ∈ R+, to, korzystając ze wzoru na pole trójkąta [tex]\frac{1}{2}[/tex]aha=[tex]\frac{1}{2}[/tex]bhb=[tex]\frac{1}{2}[/tex]chc, stwierdzamy, że a>b>c. Korzystając z nierówności trójkata a<b+c, otrzymujemy warunek, że liczby ha, hb, hc muszą spełniać nierówność [tex]\frac{1}{h_a}<\frac{1}{h_b}<\frac{1}{h_c}[/tex]. Korzystając z tej nierównosci, stwierdzamy, że zdarzeniu A sprzyjają tylko dwa zdarzenia elementarne, bo tylko odcinki o długościach 3, 5 7 oraz 5, 7, 9 mogą być wysokościami pewnego trojkata. Ponieważ |A| = 2 i [tex] |\Omega| = {{5}\choose{3}} [/tex], więc P(A) = 0,2.
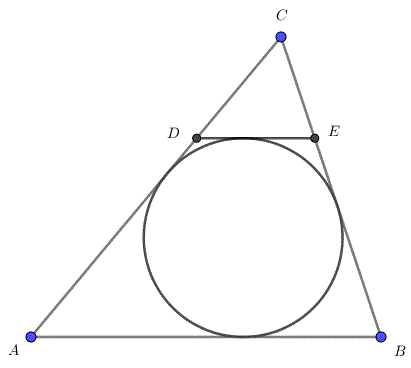
Zad. 3. Niech x oznacza długość szukanego odcinka DE, zaś c - długość boku AB równoległego do odcinka DE. Ponieważ okrąg jest wpisany w czworokąt ABED, więc |AB|+|DE| = |BE|+|AD|. Stąd wynika, że |DE|+|EC|+|CD| = |DE|+(|BC|–|BE|) + (|AC|–|AD|) = |DE|+|BC|+|AC|–(|BE|+|AD|) = |DE|+|BC|+|AC|–(|AB|+|DE|) = (|AB|+|BC|+|CA|)–2|AB| = 4–2c. Z podobieństwa trojkątów ABC i DEC mamy [tex]\frac{x}{c}=\frac{4-2c}{4}[/tex], skąd [tex] x=\frac{1}{2}c(2-c) [/tex]. Z wlasności funkcji kwadratowej otrzymujemy, że dla c = 1 długość odcinka DE jest największa i wynosi [tex]\frac{1}{2}[/tex].
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
