Zad. 1. Paczka orzeszków waży 10 dag plus ćwierć paczki orzeszków i dwa superbatony, a cztery superbatony ważą tyle, co paczka orzeszków. Ile waży paczka orzeszków?
Zad. 2. Jaś rozpoczyna grę z 250 żetonami. W każdym ruchu może:
* wymienić 10 żetonów na 2 żetony;
* wymienić 17 żetonów na 41 żetonów;
* wymienić 35 żetonów na 15 żetonów.
Z jaką najmniejszą liczba żetonów może skończyć grę?
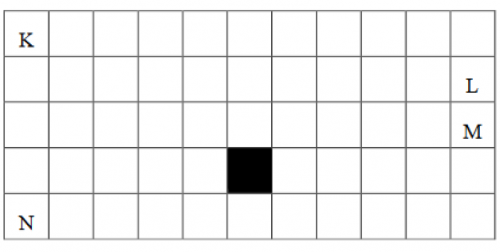
Zad. 3. Krok polega na przeniesieniu się z kwadratu, w którym się przebywa, do kwadratu sąsiadującego bokiem (czyli przemieszczeniu się o jedną kratkę w górę, w dół, na lewo lub na prawo). Ile jest najkrótszych dróg (o najmniejszej liczbie kroków):
a) z kwadratu K do kwadratu L?
b) z kwadratu K do kwadratu M?
c) z kwadratu N do kwadratu M, jeśli nie wolno przejść przez czarny kwadrat?
W tym miesiącu punkty zdobyli:
- 3 - Tomasz Tomiczek - nauczyciel z Lipowej,
- 2,5 - Bogusz Boliński I LO Kraków, Daria Bumażnik - doktoranta na Wydziale Chemii UWr, Monika Kosek - gospodyni domowa z Wrocławia, Joanna Koścień - nauczycielka z Piekar Śląskich, Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Edward Nowicki - informatyk z Poznania, Andrzej Piasecki - administrator IT z Oleśnicy, Emilia Stadnicka I LO Kraków, Michał Węgrzyn ALO PWr Wrocław,
- 1,75 - Agata Centkowska - informatyk z Biela, Agata Leśnicka - programistka z Gdańska.
Zad. 1. Paczka orzeszków waży 40 g.
Zad. 2. Najmniejsza liczba żetonów, z jaką Jaś może skończyć grę wynosi 2 (np. 25 razy 10 zamieni na 2, 5 razy 10 zamieni na 2 i jeszcze raz 10 zamieni na 2). Po każdym ruchu parzystość liczby żetonów nie zmienia się, więc nie może uzyskać 1 żetonu. Nie da się też uzyskać 0 żetonów (bo w każdym ruchu dokłada się niezerową ich liczbę).
Zad. 3. Aby przejść najkrótszą drogą:
a) z K do L trzeba wykonać 10 kroków w prawo i 1 w dół w dowolnej kolejności, tzn. z 11 koniecznych kroków trzeba wybrać jeden wykonywany w dół; takich dróg jest [tex]{{11}\choose{1}}[/tex], czyli 11.
b) z K do M trzeba wykonać 10 kroków w prawo i 2 w dół w dowolnej kolejności, tzn. z 12 koniecznych kroków trzeba wybrać dwa wykonywane w dół; takich dróg jest [tex]{{12}\choose{2}}[/tex], czyli 66.
c) z N do M w dowolny sposób trzeba wykonać 10 kroków w prawo i 2 w górę w dowolnej kolejności (wiemy już, że takich dróg jest 66), teraz wystarczy odjąć liczbę najkrótszych dróg przechodzących przez czarny kwadrat; dróg dojścia z N do tego kwadratu jest [tex]{{6}\choose{1}}[/tex], czyli 6, a dróg dojścia z tego kwadratu do M jest też 6, stąd dróg z N do M przez czarny kwadrat jest 6·6=36 (dlaczego?); szukanych dróg jest zatem 66–36 = 30.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
