Zad. 1. Suma cyfr liczby A wynosi 2023, a suma cyfr liczby B wynosi 2024. Ile wynosi reszta z dzielenia liczby 5A+2B przez 9?
Zad. 2. Cena 1 m3 gazu przed podwyżką wynosiła 1,35 zł. Po podwyżce państwo Kowalscy postanowili używać gazu w sposób bardziej ekonomiczny i jego zużycie zmniejszyło się wówczas o 10%. Mimo tego rachunek wzrósł o 8%. O ile podrożał w tym czasie gaz?
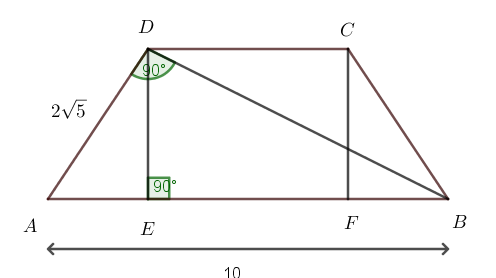
Zad. 3. Dany jest trapez równoramienny ABCD, w którym AB||CD, |AB|=10, |AD|=2√5, a przekątna BD jest prostopadła do boku AD. Ile wynosi pole trapezu ABCD?
W czerwcu punkty zdobyli:
- 3 – Eliza Banaszkiewicz SP Strzelce, Anna Frankowska SP 139 Warszawa, Aleksander Masztalski SP 3 Mikołów, Szymon Michalik SP 3 Przymierza Rodzin Warszawa, Ewa Nowakowska SP Strzelce, Karolina Piątkowska SP 16 Wrocław, Gabriela Pułecka SP 2 Brzeg Dolny, Yaraslau Sialiuk SP 82 Wrocław;
- 2 – Antoni Grębowiec SP 44 Wrocław, SP Alicja Picińska 64 Wrocław, Ignacy Włodarski SP 36 Wrocław;
- 1 – Barbara Podoba SP Tomaszów Lubelski.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Reszta z dzielenia liczby naturalnej przez 9 jest taka sama, jak reszta z dzielenia przez 9 sumy cyfr tej liczby. Zatem reszta z dzielenia przez 9 liczby 5A+2B jest taka sama, jak reszta z dzielenia przez 9 liczby 5·2023+2·2024 = 5·(2016+7)+2·(2016+8) = 7·2016+51 = 7·2016+45+6. Reszta z dzielenia liczby 5A+2B przez 9 wynosi 6.
Zad. 2. Załóżmy, że państwo Kowalscy dotychczas zużywali g m3 gazu, czyli płacili za gaz
1,35·g zł. Jeżeli cena gazu wzrosła o x złotych, to jego nowa cena jest równa 1,35+x. Zużycie spadło o 10%, zatem obecnie płacą 0,9·g·(1,35+x). Na podstawie warunków zadania otrzymujemy równanie 0,9·g·(1,35+x) = 1,08·1,35·g, skąd x=0,27 zł.
Zad. 3. Trójkąt ABD jest prostokątny, więc na podstawie twierdzenia Pitagorasa otrzymujemy
|BD|2 = 102–(2√5)2, skąd |BD|=4√5. Pole trójkąta ABD możemy obliczyć na dwa sposoby, skąd otrzymujemy równanie ½|AB|·|DE| = ½|AD|·|BD|, czyli ½·10·|DE| = ½·2√5·4√5, skąd |DE|=4. Z kolei z trójkąta prostokątnego ADE otrzymujemy na mocy twierdzenia Pitagorasa |AE|2 = (2√5)2–42, skąd |AE|=2. Zatem |CD|=10–2·2=6. Pole trapezu wynosi ½·(10+6)·4 = 32.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
