Zad. 1. Sejf skutecznie zabezpiecza przed włamaniem. Czasami jednak i przed jego właścicielem. Pan Zapominalski pamięta tylko, że szyfr do jego sejfu rozpoczyna się cyfrą 3, składa się z ośmiu niepowtarzających się cyfr i tworzy liczbę podzielną przez 15. Jakie jest prawdopodobieństwo, że Pan Zapominalski otworzy sejf za pierwszym razem?
Zad. 2. Jacek i Agatka wyruszają nad jezioro. Mają do pokonania 22 km. Jacek wyjeżdża na rowerze z prędkością 10 km/h, ale po przejechaniu kilku kilometrów zostawia rower i idzie dalej pieszo z prędkością 6 km/h. Agatka wyrusza pieszo z prędkością 5 km/h, dochodzi do roweru i jedzie na nim z prędkością 12 km/h. Ile minut rower nie był używany, jeżeli Jacek i Agatka wyruszyli na jezioro jednocześnie, pokonali tę samą drogę i przybyli na miejsce jednocześnie?
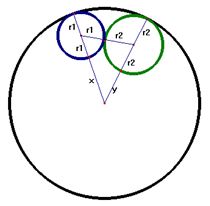
Zad. 3. Dwa okręgi o różnych promieniach są zewnętrznie styczne do siebie nawzajem i oba są styczne wewnętrznie do trzeciego okręgu o średnicy 20 cm. Środki tych okręgów są wierzchołkami trójkąta. Oblicz obwód tego trójkąta.
W marcu punkty zdobyli:
- 3 – Kosma Kasprzak G 58 Poznań, Szymon Bar PG 1 Głogówek, Bartłomiej Bychawski G Akademickie PWr, Jakub Dobrzański G 3 Lubin, Julia Grzyb G Wieliszew, Igor Hołowacz G Akademickie PWr, Alex Kalinowski G Dwujęzyczne Góra, Tomasz Lefler ZSS Wołów, Krzysztof Nawrocki G Bóbrka, Michał Piórkowski G Urszulanek Wrocław, Małgorzata Plewka G Akademickie PWr, Laura Stefanowska G im. Św. Franciszka z Asyżu Legnica, Michał Szwej G Dwujęzyczne Chorzów i Julia Waleńdzik PG 1 Brzeg Dolny;
- 2 – Krzysztof Możdżeń ZSO 1 Żory, Maciej Płonka G Akademickie PWr, Kacper Słoniec G52 Kraków, Jan Jancewicz G Akademickie PWr, Łukasz Janiak G Akademickie PWr, Mikołaj Mastaliński G Akademickie PWr, Magdalena Owczarek PZSO Legionowo i Julia Mazur G Lewin Brzeski,
- 1 - Gracjan Ciupa G 10 Wrocław, Jakub Rudzik G Akademickie PWr i Kacper Misiaczek G Akademickie PWr.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Liczba jest podzielna przez 15, gdy dzieli się przez 3 i 5. Szukany szyfr ma postać:
3 - - - - - - 0 lub 3 - - - - - - 5.
Suma wszystkich cyfr wynosi: 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 i jest podzielna przez 15. Szyfr składa się z ośmiu cyfr zatem możemy odrzucić dwie cyfry, których suma jest podzielna przez 3, wówczas suma pozostałych ośmiu również będzie podzielna przez 3.
W przypadku 3 - - - - - - 0 możemy odrzucić: 1 i 2; 1 i 5; 1 i 8; 2 i 4; 2 i 7; 4 i 5; 4 i 8; 5 i 7; 6 i 9; 7 i 8.
Pozostałe 6 cyfr (między cyframi 3 i 0) można ustawić na 6! = 1 . 2 . 3 . 4 . 5 . 6 =720 sposobów.
Mamy zatem 10 . 6! = 7 200 możliwości.
W przypadku 3 - - - - - - 5 możemy odrzucić: 0 i 6; 0 i 9; 1 i 2; 1 i 8; 2 i 4; 2 i 7; 4 i 8; 6 i 9; 7 i 8.
Pozostałe 6 cyfr (między cyframi 3 i 5) można również ustawić na 6! sposobów.
Mamy zatem 9 . 6! = 6 480 możliwości.
Wszystkich możliwych sytuacji jest 7 200 + 6 480 = 13 680.
Prawdopodobieństwo, że Pan Zapominalski otworzy sejf za pierwszym razem wynosi 1/13 680.
Zad. 2. Każde z nich jedzie na rowerze dwa razy szybciej niż drugie idzie. Czas t, kiedy rower nie jest używany jest jednocześnie czasem jazdy Jacka na rowerze, bo Agatka potrzebuje dwa razy więcej czasu 2t na dojście do roweru (idzie dwa razy wolniej niż Jaś jedzie). Czas t jest również czasem jazdy Agatki od momentu dojścia do roweru do końca trasy, bo Jaś potrzebuje dwa razy więcej czasu na dojście do końca trasy (czas t gdy rower nie jest używany dodać czas t jazdy Małgosi).
Trasę jaką pokonuje Jacek możemy zapisać: 10t + 6 . 2t
Z równania 10t + 6 . 2t = 22 otrzymujemy t = 1. Rower jest nieużywany przez 60 minut.
Zad. 3. Niech r1, r2 – promienie okręgów stycznych zewnętrznie, R – promień trzeciego okręgu.
Wówczas R = 2r1+x = 10 i R = 2r2+y = 10 a obwód trójkąta: O∆ = 2r1+x + 2r2+y = 10 + 10 = 20.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
