luty 2017

luty 2017

Data ostatniej modyfikacji:
2018-09-17

Począwszy od tego odcinka rozwiązania zadań prosimy przesyłać na adres mejlowy yolande@poczta.fm (adres pocztowy pozostaje bez zmian).

Zad. 1. Wykaż, że dla dowolnej liczby naturalnej n liczba [(n+4)/2] + 3n – 2·(-1)ⁿ jest podzielna przez 7, gdzie [a] oznacza część całkowitą liczby a.

Zad. 2. Wyznacz wszystkie pary liczb pierwszych p i q, dla których spełnione jest równanie p²–42q² = 1.

Zad. 3. Który z równoległoboków wpisanych w prostokąt o bokach długości 6 i 8, o bokach równoległych do przekątnych tego prostokąta, ma największy obwód? Ile on wynosi?

W lutym punkty zdobyli:

3 - Katarzyna Penkalska G Wieliszew, Karolina Mielczarek G Lewin Brzeski, Szymon Bar PG 1 Głogówek,Jakub Dobrzański G 3 Lubin, Julia Grzyb G Wieliszew, Mateusz Jankowski G 77 Warszawa, Igor Hołowacz G Akademickie PWr, Jan Jancewicz G Akademickie PWr, Łukasz Janiak G Akademickie PWr, Alex Kalinowski G Dwujęzyczne Góra, Tomasz Lefler ZSS Wołów, Mikołaj Mastaliński G Akademickie PWr, , Kacper Misiaczek G Akademickie PWr, Michał Piórkowski G Urszulanek Wrocław, Małgorzata Plewka G Akademickie PWr, Jakub Rudzik G Akademickie PWr, Krzysztof Palatyński G Filomata, Michał Szwej G Dwujęzyczne Chorzów i Julia Waleńdzik PG 1 Brzeg Dolny;
2,5 - Gracjan Ciupa G 10 Wrocław i Jakub Musiała G Akademickie PWr
2 - Bartłomiej Bychawski G Akademickie PWr i Krzysztof Nawrocki G Bóbrka;
1,5 - Katarzyna Siomka G Lewin Brzeski, Kacper Słoniec G 52 Kraków i Jakub Rozmarynowski G1 Żory;
1 - Krzysztof Mach G 52 Kraków i Szymon Kowaliński G Akademickie PWr.

Pozostali uczestnicy otrzymali poniżej 1 punktu.

Rozwiązania zadań

Zad. 1. Jeżeli n jest liczbą parzystą to: n = 2k, k ∈ N, wówczas otrzymujemy:
[(2k + 4)/2] + 3 ^.2k – 2 ^. (-1)^2k = [k + 2] + 6k – 2 = k + 2 + 6k – 2 = 7k,
zatem liczba jest podzielna przez 7.
Jeżeli n jest liczbą nieparzystą to: n = 2l + 1, l ∈ N i liczba przyjmuje postać:
[(2l + 1 + 4)/2] + 3 ^. (2l + 1) – 2 ^. (-1)^2l+1 = [(2l + 5)/2] + 6l + 2 = [l +2,5] + 6l+ 5 = l + 2 + 6l +5 =7(l + 1)
zatem jest podzielna przez 7.

Zad. 2. Z równania p² – 42q² = 1 wynika, że liczba p jest liczbą nieparzystą . Równanie p² – 42q²= 1 jest równoważne równaniu 42q² = p² – 1 (w zbiorze R²) i p² – 1 = (p – 1)(p + 1), więc prawa strona równania 42q² = p² – 1 dzieli się przez 4 (jako iloczyn liczb parzystych p – 1 i p + 1. Stąd wynika, ze lewa strona równania 42q² = p² – 1 dzieli się przez 4, a to jest możliwe tylko wtedy, gdy q = 2. Jeżeli q = 2 to p = 13. Równanie spełnia jedna para liczb pierwszych p = 13 i q = 2.

Zad. 3.

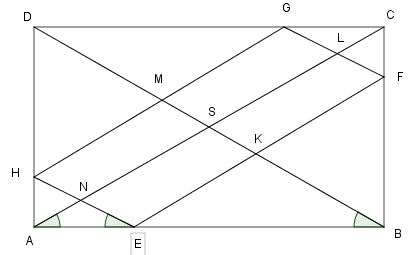
Przekątne w prostokącie przecinają się w połowie swojej długości, zatem ∡BAS ≡∡ABS. Ponieważ HE||BD, więc ∡SBA ≡∡NEA. Wobec tego △AEN jest równoramienny i |AN| = |NE|. Analogicznie dowodzimy, że |LF| = |LC|. Zatem |NE| +|EF| + |LC| = |AC| a szukany obwód wynosi 2|AC|. Na podstawie twierdzenia Pitagorasa |AC|² = 6² + 8², czyli |AC| = 10 a obwód szukanego równoległoboku wynosi 20. Każdy z równoległoboków wpisanych w ten prostokat o bokach równoleglych do przekątnych ma obwód o długości 20.

Dodaj komentarz

Zadanie 3

Michał (niezweryfikowany), sobota, 04/02/2017 - 23:34

Dzień dobry,
Czy mógłbym prosić o wyjaśnienie mojej wątpliwości dotyczącej zadania 3:
Czy równoległobok wpisany w prostokąt, to taki, którego wszystkie wierzchołki leżą na bokach tego prostokąta?
Dziękuję i pozdrawiam.