Zad. 1. Po której stronie znajdują się guziki w ubraniach damskich, a po której w męskich? Dlaczego?
Zad. 2. Ile cyfr ma liczba 2024!? Iloma zerami jest zakończona?
Zad. 3. Jak za pomocą standardowych wykresów funkcji narysować na ekranie okrąg o danym środku i danym promieniu? Dlaczego może wyglądać on dziwnie? Jak temu zaradzić?
W tym miesiącu punkty zdobyły panie:
- 2,75 pkt. - Krystyna Lisiowska - redaktor z Warszawy,
- 2,25 pkt. - Marzena Wąsiewicz - nauczycielka z Kajetan.
Zad. 1. Guziki w ubraniach damskich znajdują się po lewej stronie, a w męskich - po prawej. Początkowo bluzki zapinane na guziki były towarem luksusowym i nosiły je wyłącznie panie z wyższych sfer, które ubierały pokojówki, a tym o wiele łatwiej było zapinać guziki znajdujące się po lewej stronie. Ponadto damy te często jeździły konno, siedząc bokiem. Wysuwały wówczas prawą stroną ciała do przodu i nie musiały martwić się o to, że ich kreacje się rozepną. Zapinane na lewą stronę ubrania cieszą się także uznaniem karmiących piersią matek. Kobieta trzyma dziecko lewą ręką i rozpina koszulę prawą. Gdy guziki stały się standardem także w biednych domach, kobiety wszywały je po lewej stronie, aby naśladować bogate damy. Z kolei koszule męskie projektowano tak, aby użytkownicy mogli je samodzielnie zapinać. Poza tym panowie nosili szable i miecze po lewej stronie, aby prawą ręką można było szybko po nie sięgnąć. Jeśli ubrania zapinane byłyby na lewą stronę, istniało ryzyko, że broń zawadzi o odzież.
Zad. 2. Liczba 2024! ma 5815 cyfr i kończy się 503 zerami.
Zad. 3. Do rysowania okręgu można użyć opcji wykresów kartezjańskich. Wówczas półokrąg górny i dolny należy wyświetlać jako osobne funkcje: Y1 = sqrt(r^2–(x–a)^2)+b, Y2 = -Y1+2b.
Okrąg może wtedy wyglądać jak elipsa, jeśli zakresy na osiach OX i OY ustawione będą tak, że jednostki na osiach nie będą równe. Programy rysujące wykresy mają na ogół automatyczne ustawienia wyrównujące jednostki na osiach (np. zoom square). Inny problem to stromość wykresu w okolicy punktów połączenia. Jesli jest duża, okrąg wygląda na przerwany w tych miejscach.
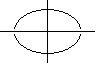
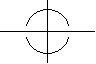
Wygodniejszym sposobem rysowania okręgu jest użycie układu równań parametrycznych X1(t) = a+rcos(t),Y1(t) = b+rsin(t) lub układu współrzędnych biegunowych R1(θ) = r. Zastrzeżenia elipsowatego kształtu dotyczą także tych równań. Dodatkowo w tych równaniach trzeba ustawić krok, z jakim zmienia się argument kątowy. Jeśli ten krok będzie za duży - okrąg będzie przypominał wielokąt (w opcji łączenia punktów wykresu odcinkiem) lub pojedyncze punkty ułożone na okręgu (w opcji braku łączenia punktów wykresu).
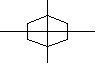
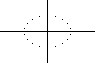




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
