Zad. 1. Między dwoma budynkami stoi drabina. Jest tak umieszczona, że jeśli ją pochylić w stronę jednego domu, to sięga okna na wysokości 12 metrów, a jeśli w stronę drugiego, to sięga zaledwie 9 metrów od poziomu ulicy. Oba położenia drabiny są prostopadłe. Jaka jest długość drabiny i szerokość ulicy?
Zad. 2. Tomek stoi na peronie o długości 340 m i czekając na pociąg, rozmyśla. Przypuśćmy, że pociąg potrzebuje 6 sekund, aby przejechać obok mnie ze stałą prędkością. Przypuśćmy, że między chwilą, w której lokomotywa dotrze do początku peronu, a chwilą, w której tylne światło ostatniego wagonu minie koniec peronu, upłyną dokładnie 23 sekundy. Jaka jest długość pociągu i z jaką jedzie on prędkością?
Zad. 3. Jaka funkcja f spełnia dla dowolnej liczby rzeczywistej x równość f (x) + 2 f (1−x) = x2 ?
W październiku punkty zdobyli:
- 3 pkt. – Joanna Lisiowska XXI LO Warszawa, Zuzanna Szymańska VIII LO Wrocław;
- 2,5 pkt. – Marcin Wiśniewski LO Ząbkowice Śląskie
- 2 pkt. – Bartłomiej Zug LO Olesno, Jakub Dobrzański I LO I Lubin, Mikołaj Zapotoczny LO Ząbkowice Śląskie.
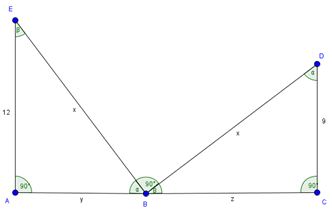
Zad. 1. Oznaczmy |∡ABE| = α i |∡CBD| = β. Mamy α+β = 90º, a stąd |∡AEB| = β i |∡BDC| = α. Trójkąty ABE i CBD są więc podobne (cecha kkk), a stąd y/x = 9/x, więc y=9 oraz 12/x = z/x, więc z=12. Zatem szerokość ulicy to 12+9 = 21 metrów. Na podstawie twierdzenia Pitagorasa mamy x2 = 122 + 92, czyli x = 15, więc długość drabiny wynosi 15 metrów.
Zad. 2. W ciągu 6 sekund czoło pociągu pokonuje odległość równą długości pociągu, a w ciągu 23 sekund - pokonuje odległość równą łącznej długości peronu i pociągu. Niech d onacza długość pociągu, a v - jego prędkość. Wówczas v = d/6 i v = 340+d/23. Z tego układu równań wyliczamy długość pociągu równą 120 m i jego prędkość równą 20 m/s.
Zad. 3. Dla argumentów x i 1–x możemy zapisać warunki:
[tex]\left\{\begin{array}{rcl}f(x)+2f(1-x)&=&x^2\\f(1-x)+2f(1-(1-x))&=&(1-x)^2\end{array}\right.[/tex]
lub równoważnie
[tex]\left\{\begin{array}{rcl}f(1-x)&=&0,5x^2-0,5f(x)\\f(1-x)+2f(x)&=&1-2x+x^2\end{array}\right.[/tex]
Podtawiając z I równania do II otrzymujemy jedno równanie 0,5x2 – 0,5 f (x) + 2 f (x) = 1 – 2x + x2,
z którego wyliczamy f (x) = 1/3x2 – 4/3x + 2/3.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
