Zad. 1. Znajdź wszystkie k∈N, dla których 2k + 1472 jest kwadratem liczby naturalnej.
Zad. 2. Oblicz pole największego trójkąta wpisanego w okrąg o danym promieniu długości r.
Zad. 3. Wyznacz wszystkie prostopadłościany, których długości krawędzi są liczbami całkowitymi, a pole powierzchni jest liczbowo równe sumie długości krawędzi.
W listopadzie punkty zdobyli:
- 3 pkt. – Joanna Lisiowska XXI LO Warszawa;
- 2 pkt. – Zuzanna Szymańska VIII LO Wrocław, Jakub Dobrzański I LO Lubin, Bartłomiej Zug LO Olesno, Marcin Wiśniewski LO Ząbkowice Śląskie
- 1,5 pkt. – Mikołaj Zapotoczny LO Ząbkowice Śląskie.
Zad. 1. Mamy 1472 = 26 . 23, zatem szukamy takiego k, że 2k+26·23 = n2, gdzie (k, n ∈ N). Równoważnie 26·(23+2k-6) = n2. Ponieważ pierwszy czynnik jest już kwadratem, drugi też musi nim być, czyli 2k-6 + 23 = r2, gdzie r ∈ N. Szukamy zatem liczby x, dla której 2x+23= r2. Jeżeli x ≥ 3, to reszta z dzielenia 2x przez 8 wynosi 0, a wtedy reszta z dzielenia 2x+23 przez 8 wynosi 7. Jednak reszta z dzielenia kwadratów przez 8 może być równa tylko 0, 1 lub 4. Dlaczego? Wobec tego x≤2, czyli k≤8. Sprawdzając po kolei wszystkie wartości k, widzimy, że tylko k=7 spełnia warunki zadania, zachodzi bowiem 1472 + 27 = 1600 = 402.
Zad. 2. Największym trójkątem wpisanym w dany okrąg jest trójkąt równoboczny. Załóżmy, że tak nie jest. Niech w wierzchołku C stykają się boki a i b o różnej długości. Wówczas przesuwamy po okręgu punkt C tak, aby boki te wyrównać (ruch w górę do położenia na symetralnej boku c). W tym procesie rośnie wysokość trójkąta opuszczona na bok c, a długość tego boku się nie zmienia, zatem rośnie pole trójkąta. Stąd wniosek, że wyjściowy trójkąt nie mógł mieć największego możliwego pola.
Ponieważ dla trójkąta równobocznego h = 3/2r = a√3/2, mamy a = √3r, a szukane pole wynosi $\frac{3r^2\sqrt{3}}{4}$.
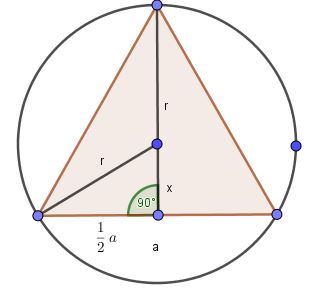
Można jednak mieć wątpliwości, czy spośród wszystkich trójkątów wpisanych w dany okrąg istnieje w ogóle trójkąt o największym polu. Wykażemy to rachunkowo. Niech h jest wysokością trójkąta opuszczoną na bok a. Z twierdzenia Pitagorasa mamy $\frac{a}{2}=\sqrt{r^2-(h-r)^2}$, czyli pole trójkąta wyraża się jako $P(h)=h\sqrt{r^2-(h-r)^2}.$
Szukamy wartości maksymalnej tej funkcji. W tym celu obliczmy jej pochodną i przyrównajmy do zera. W rachunkach stosujemy wzór na pochodną iloczynu oraz pochodną funkcji złożonej. [tex]P'(h)=\sqrt{r^2-(h-r)^2}-\frac{2h(h-r)}{2\sqrt{r^2-(h-r)^2}}=0[/tex].
Stąd [tex]\sqrt{r^2-(h-r)^2}=\frac{h(h-r)}{\sqrt{r^2-(h-r)^2}}[/tex] i r2–(h–r)2>0, bo r > h–r.
Zatem r2–(h–r)2 = h(h–r), a stąd 2h2=3hr, więc h=3/2r, czyli rzeczywiście otrzymujemy trójkąt równoboczny.
Zad. 3. Niech x, y, z będą długościami krawędzi prostopadłościanu (x ≤ y ≤ z). Z warunków zadania otrzymujemy równanie xy+yz+zx = 2(x+y+z), które rozwiązujemy w liczbach całkowitych dodatnich. Jeżeli trójka (x, y, z) jest rozwiązaniem równania, to x ≤ 2, bo w przeciwnym razie zachodziłoby xy+yz+zx > 2x+2y+2z. Zatem x∈{1, 2}. Dla x=1 mamy y+yz+z = 2(x+y+z), czyli (y–1)(z–1) = 3, skąd y=2 i z=4. Dla x=2 mamy yz=4, skąd y=z=2. Wyjściowe równanie jest więc spełnione przez trójki (1, 2, 4) i (2, 2, 2), co daje dwa prostopadłościany spełniające warunki zadania.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
