Zad. 1. Piramidę z rysunku zbudowano z pierwszych piętnastu liczb naturalnych rozmieszczonych w losowym porządku. Liczby te należy przestawić tak, aby pięć liczb na każdym boku trójkąta dawało jednakową sumę. Ile wynosi największa taka suma?
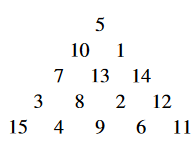
Zad. 2. 1 X 2022 na Zamku Książ odbył się jubnileuszowy XX Matematyczny Marsz na Orientację. Od 20 lat jest on rozgrywany w pierwszą sobotę października. Jaki dzień tygodnia wypadnie w setną rocznicę XX Marszu?
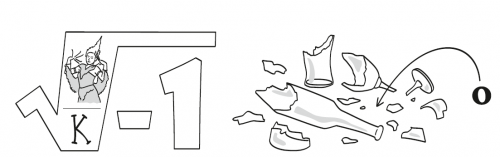
Zad. 3. Rozwiąż rebus.
W tym miesiącu punkty zdobyli:
- 3 - Daria Bumażnik - doktorantka na Wydziale Chemii UWr, Elżbieta Grzechnik - emerytowana nauczycielka z Radomia, Monika Kosek - gospodyni domowa z Wrocławia, Joanna Koścień - nauczycielka z Piekar Śląskich, Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Edward Nowicki - informatyk z Poznania, Andrzej Piasecki - administrator IT z Oleśnicy, Emilia Stadnicka I LO Kraków, Adrian Szumski - inżynier mechanik z Płocka, Bartosz Tłok - nauczyciel z Mikołowa, Adrianna Tokarska - data scientist z Krakowa, Tomasz Tomiczek - nauczyciel z Lipowej, Michał Węgrzyn ALO PWr Wrocław, Janusz Wieczorek - emerytowany nauczyciel z Sandomierza, Dominik Zygmunt - specjalista ds administrowania wierzytelnościami z Białej Rawskiej,
- 2 - Natalia Lodzińska SP 41 Kraków,
- 1 - Bogusz Boliński I LO Kraków, Krzysztof Danielak - programista z Jeleniej Góry, Agata Leśnicka - programistka z Gdańska, Igor Wojtasik I LO Jelenia Góra.
Pozostałym zawodnikom nie przyznano punktów.
Zad. 1. Największa możliwa suma liczb na jednej krawędzi trójkąta wynosi 52. Najmniejsze liczby (1, 2 i 3) należy ustawić w środku trójkąta, bo nie wchodzą do sumowania. Największe (15, 14 i 13) należy wstawić w wierzchołkach, bo wchodzą do sumy dwukrotnie (na każdym z boków). Po ustawieniu wierzchołków sumy na bokach wynoszą 29, 28 i 27, a suma niewykorzystanych liczb wynosi 4+5+6+7+8+9+10+11+12 = 72. Trzeba te liczby podzielić na zbiory trzyelementowe o sumach 23, 24 i 25, co na bokach da stałe sumy 52. Jest to wykonalne, co pokazuje diagram poniżej.
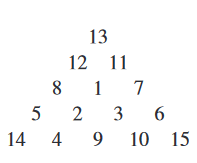
Zad. 2. Setna rocznica XX Marszu wypada 1 X 2122, czyli za 100·365+(25–1) = 36524 dni (bo rok 2100 nie jest przestępny). 36524 = 35000 + 1400 + 100 + 21 + 3 = 35000 + 1400 + (70+28+2) + 21 + 3 jest podzielne przez 7 z resztą 5, zatem 100 rocznica Marszu wypada 5 dni po sobocie, czyli w czwartek.
Zad. 3. Witaj szkoło! (w - I - Tajka/KA - szkło - O wrzuć w środek)
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
Pytanie
Czy w zad. 3 Zamiast k nie powinno być m?
Odp.
Nie.