Zad. 1. Liczby palindromiczne to takie liczby naturalne, które nie zmieniają wartości czytane wprost i wspak. Ile jest palindromicznych liczb trzycyfrowych, które są jednocześnie kwadratami liczb naturalnych? Jakie to liczby?
Zad. 2. Każdy z spośród 22 uczestników grzybobrania znalazł przynajmniej jeden grzyb. Borowiki znalazło 14 osób, podgrzybki - 18 osób, a maślaki - 16. Ilu co najwyżej było takich grzybiarzy, którzy zebrali grzyby każdego z trzech gatunków?
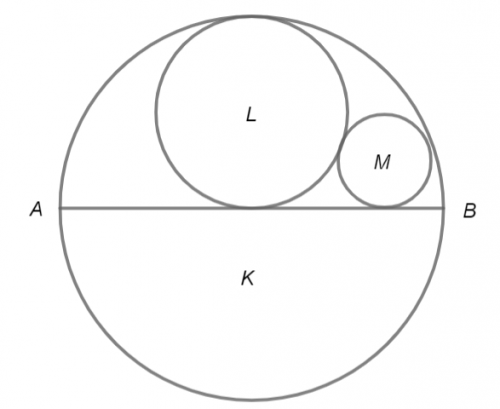
Zad. 3. Okrąg K o średnicy AB jest styczny do okręgu L, który jest styczny do AB w jego środku. Okrąg M jest styczny do okręgów K i L oraz do odcinka AB. Oblicz stosunek pól kół ograniczonych okręgami K i M.
W październiku punkty zdobyli:
- 3 – Artur Bumażnik ZS Elektronicznych Jelenia Góra, Zuzanna Czapiewska ZSB Słupsk, Oliwier Gajda LO Dobrzeń Wielki, Paweł Idzikowski I LO Ostrzeszów, Jagoda Janiś LO Góra, Joanna Nowakowska LO Aslan Głogów, Stanisław Pająk LO Żary, Paweł Prasol III LO Leszno, Mieszko Ratajczak II LO Głogów, Oliwier Roszkowski X LO Wrocław, Aleksandra Strzelecka LO Jarocin, Igor Sudyka V LO Kraków, Miłosz Zakrzewski LO Tuchola;
- 2 – Emilia Cichowska II LO Lubin, Aleksander Kiszkowiak I Technikum Elektroniczne Warszawa, Miriam Sara Olbrych II LO Oleśnica, Gabriela Pułecka V LO Wrocław, Cezary Rębiś ZS Elektronicznych Radom, Brajan Woźniak II LO Oleśnica;
- 1 – Hubert Kosmala II LO Oleśnica, Anna Niżałowska LO Góra, Paulina Wójcik LO Dobrzeń Wielki.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Liczby trzycyfrowe, które są kwadratami liczb naturalnych, to 102 = 100, 112 = 121, 122 = 144, 132 = 169, …, 282 = 784, 292 = 841, 302 = 900, 312 = 961. Aby liczba była palindromiczna, cyfra jedności musi być taka sama jak cyfra setek. Wśród liczb kwadratowych są trzy takie liczby: 121, 484 i 676.
Zad. 2. Oznaczmy liczby osób, które znalazły grzyby poszczególnych gatunków przez:
- B - borowiki, |B|=14
- M - maślaki, |M|=16
- P - podgrzybki, |P|=18.
Wtedy łączna liczba uczestników grzybobrania to |B∪M∪P|=22. Chcemy znaleźć maksymalną liczbę osób, które znalazły wszystkie trzy gatunki grzybów, czyli największą możliwą wartość
|B∩M∩P|. Skorzystamy z zasady włączeń i wyłączeń.
|B∪M∪P| = |B|+|M|+|P|−|B∩M|−|B∩P|−|M∩P|+|B∩M∩P|
Zauważmy, że po prawej stronie wzoru każdy uczestnik grzybobrania jest liczony tylko raz. Podstawiamy wartości, które znamy: 22 = 14+16+18−|B∩M|−|B∩P|−|M∩P|+|B∩M∩P|, czyli
|B∩M|+|B∩P|+|M∩P|–26 = |B∩M∩P|. Największa możliwa wartość |B∩M∩P| wynosi 14 (dlaczego?), ale ta liczba nie spełnia warunków zadania, bo wtedy 14+14+|M∩P|–26 = 14, czyli |M∩P|=12, a to jest niemożliwe (dlaczego?). Sprawdźmy wobec tego |B∩M∩P|=13. Wówczas równość |B∩M|+|B∩P|+|M∩P|–26 = |B∩M∩P| zachodzi dokładnie wtedy, gdy
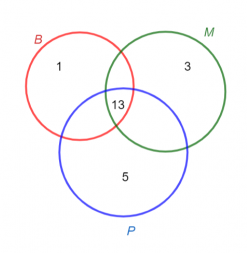
|B∩M|=|B∩P|=|M∩P|=13, co jest możliwe w sytuacji przedstawionej na diagramie poniżej. Zatem maksymalna liczba osób, które znalazły wszystkie trzy gatunki grzybów, wynosi 13.
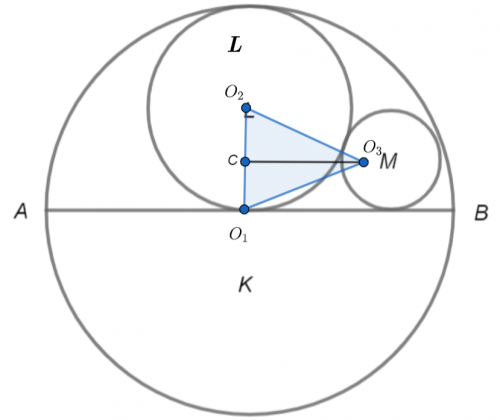
Zad. 3. Niech punkty O1, O2, O3 będą odpowiednio środkami okręgów K, L, M. Z warunków zewnętrznej i wewnętrznej styczności wynika, że: |O1O2| = r2 = 1/2r1, |O2O3| = r2+r3 = 1/2r1+r3, |O1O3| = r1–r3. W trójkącie O1O2O3 poprowadźmy wysokość na bok O1O2 i niech C będzie jej spodkiem. Wówczas |O1C|= r3 oraz |O2C| = r2–r3 = 1/2r1–r3. Z twierdzenia Pitagorasa zastosowanego do trójkątów prostokątnych O1O3C i O3O2C otrzymujemy: |CO3|2 = |O1O2|2–|O1C|2 i |CO3|2 = |O2O3|2–|O2C|2. Odejmując stronami te równości, otrzymamy 0 = |O1O3|2–|O1C|2–|O2O3|2+|O2C|2, czyli 0 = (r1–r3)2–r32–(1/2r1+r3)2+(1/2r1–r3)2. Równość ta jest równoważna warunkowi r12–4r1r3 = 0, skąd r1= 4r3. Wówczas stosunek pola K do pola koła M wynosi r12: r32 = (4r3)2:r32 = 16.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
