Programowanie liniowe jest metodą podejmowania optymalnych decyzji w zagadnieniach ekonomicznych przy ustalonych warunkach i ograniczeniach. Oto przykład takiej sytuacji.
Przykład 1. Farmer zgromadził zapas 1000 balotów siana. Na wykarmienie byka potrzeba 15 balotów, a na wykarmienie kozy 3 balotów siana. Na sprzedaży byka hodowca zarobi 1080 zł, a na sprzedaży kozy 210 zł. Jakie zwierzęta i w jakiej liczbie powinien hodować, aby wystarczyło mu siana i jego zysk był największy?
Rozwiązanie. Byk zjada 15 balotów i daje zysk 1080 zł, czyli hodując byki, na jednym balocie siana zarabia się 1080/15 = 72 zł. Koza zjada 3 baloty i daje zysk 210 zł, więc hodując kozy na jednym balocie siana zarabia się 210/3 = 70 zł. Widać, że hodowla byków jest bardziej opłacalna niż kóz, zatem trzeba zmaksymalizować liczbę byków na farmie. Ale 1000 balotów siana wystarczy na wykarmienie tylko 66 byków (bo 1000/15≈66,666). Zostanie jeszcze 1000-66·15 = 10 balotów siana, którym można wykarmić jeszcze 3 kozy. Zatem w celu zmaksymalizowania zysku farmer powinien hodować 66 byków i 3 kozy. Jego zysk wyniesie wtedy 66·1080+3·210 = 71280+630 = 71910 zł i zostanie mu jeszcze jeden balot siana.
Ograniczenia występujące w tym zadaniu opisywał warunek B·15+K·3 ≤ 1000, a zysk farmera opisywało wyrażenie B·1080+K·210, gdzie B to liczba byków, a K - liczba kóz, jakie powinien hodować farmer. Niewiadome B i K są w tych wzorach mnożone przez pewne liczby i dodawane, występują bez żadnych potęg i nie są mnożone jedna przez drugą. Takie wyrażenia nazywa się zależnościami liniowymi. W gimnazjum uczy się rysowania wykresów takich zależności. Okazuje się, że są one zawsze liniami prostymi.
[koniec wykładu dla SP]
Przedstawmy zależności z poprzedniego zadania w sposób graficzny. Chcemy zmaksymalizować wartość zysku, czyli zależności liniowej Z= B·1080+K·210, przy następujących warunkach: B≥0, K≥0 i B·15+K·3 ≤ 1000. Podany układ warunków - nierówności opisuje (na płaszczyźnie z układem współrzędnych BOK) pewien trójkąt.
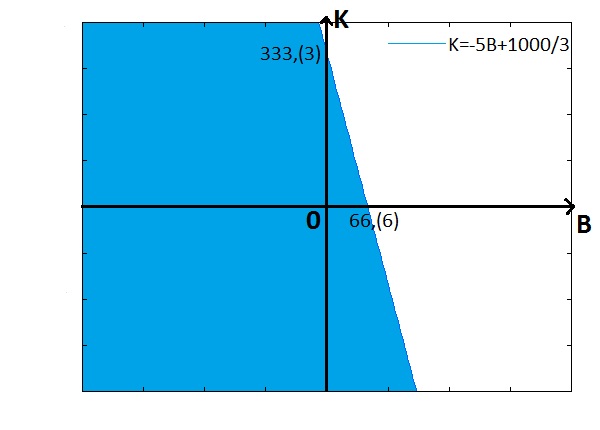
Dla każdego punktu o współrzędnych (b, k) z tego trójkąta, można obliczyć zysk farmera Z. Metoda programowania liniowego gwarantuje, że największa i najmniejsza wartość Z będą przyjmowane w wierzchołkach tego trójkąta. Wystarczy zatem sprawdzić tylko trzy możliwości: (0, 0), (0, 3331/3) oraz (662/3, 0). Zysk dla każdej z nich wynosi odpowiednio 0 zł, 70000 zł i 72000 zł i jest największy przy hodowli samych byków, ale nie można przecież hodować 2/3 byka, dlatego zamieniamy tę część na 3 kozy, osiągając nieco niższy zysk od maksymalnego 71910 zł.
Metoda programowania liniowego pozwala maksymalizować lub minimalizować wartość pewnej zależności liniowej Z(x, y) zwanej funkcją celu, przy ustalonych warunkach na x i y będących układem nierówności liniowych, który w układzie kartezjańskim opisuje pewien wielokąt nazywany obszarem rozwiązań dopuszczalnych. Z niego wybieramy rozwiązanie optymalne (największe lub najmniejsze), sprawdzając, jakie wartości przyjmuje funkcja celu we wszystkich wierzchołkach. Dobrze ilustruje to kolejny przykład.
Przykład 2. Pewien rzemieślnik produkuje patelnie i czajniki, do których wytworzenia zużywa blachę i plastik. Do wyprodukowania patelni potrzeba 2 kg blachy i 1 kg plastiku, a do produkcji czajnika - 2 kg blachy i 2 kg plastiku. Rzemieślnik posiada w magazynie 14 kg blachy i 8 kg plastiku. Zysk z produkcji patelni to 20 zł, a z produkcji czajnika 30 zł. Co powinien produkować rzemieślnik i w jakiej ilości, aby wykorzystując zapasy surowców, zmaksymalizować swój zysk?
Rozwiązanie. Zapiszemy powyższy problem w języku programowania liniowego. Oznaczmy przez x liczbę produkowanych patelni, a przez y - liczbę czajników. Funkcja celu, którą chcemy zmaksymalizować, to zysk osiągany dla konkretnych wartości x i y, czyli Z(x, y) = 20x+30y. Mamy też warunki ograniczające. Oczywiście x≥0 i y≥0, bo wielkość produkcji nie może być ujemna. Jesteśmy też ograniczeni ilością posiadanych surowców. Blachy mamy 14 kg, a na każdą patelnię i czajnik zużywamy jej po 2 kg, stąd 2x+2y ≤ 14. Plastiku mamy tylko 8 kg i zużywamy 1 kg na patelnię i 2 kg na czajnik, czyli x+2y ≤ 8. Teraz warunki ograniczające umieszczamy na wykresie.
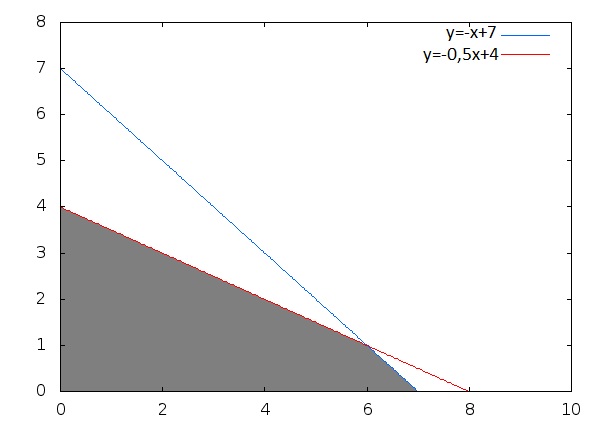
Zajmujemy się tylko I ćwiartką układu współrzędnych (bo x≥0 i y≥0). Warunek na ilość blachy daje ograniczenie obszaru dopuszczalnych rozwiązań prostą 2x+2y = 14, czyli y = -x+7 (linia niebieska), a warunek na ilość plastiku daje ograniczenie prostą x+2y = 8, czyli y= - x/2 +4 (linia czerwona). Nierówności w obu przypadkach dają na wykresie obszar po lewej stronie tych prostych. Część wspólna wszystkich warunków, czyli rozwiązanie układu nierówności, jest zaznaczone na szaro. Proste niebieska i czerwona przecinają się w punkcie o współrzędnych (6, 1). Teraz z obszaru rozwiązań dopuszczalnych chcemy wybrać rozwiązanie optymalne, które zmaksymalizuje zysk rzemieślnika. Wiemy już, że punkt o największej funkcji celu leży nad jednym z wierzchołków szarego czworokąta, czyli nad jednym z punktów (0, 0), (0, 4), (6, 1), (7, 0). Sprawdzając wartości Z(x, y) dla każdego z tych punktów, otrzymujemy kolejno wartości 0, 120, 150, 140. Zatem rzemieślnik zmaksymalizuje swój zysk, produkując ze zgromadzonych surowców 6 patelni i 1 czajnik.
[koniec wykładu dla GIM]
Zapewne dziwisz się, dlaczego sztuczka ze sprawdzaniem wartości funkcji celu dla wierzchołków wielokąta zawsze działa i dlaczego pozwala znaleźć ekstremalne wartości. Wyjaśnienie tej zagadki jest bardzo łatwe. W jego zrozumieniu pomoże ci prosty eksperyment. Ponieważ funkcja celu jest zależnością liniową, jej wykresem (w przestrzeni) jest płaszczyzna (podobnie jak wykresem zależności liniowej na płaszczyźnie jest prosta). Jeśli umieścisz model płaszczyzny (np. kartkę papieru nachyloną pod dowolnym kątem) nad jakimś wielokątem narysowanym na poziomym stole, to po zrzutowaniu go (w kierunku prostopadłym do blatu) na kartce też powstanie wielokąt (naszkicuj go). Jego boki leżą nad bokami wyjściowego wielokąta, a wierzchołki - nad wierzchołkami). Gdy poruszamy się po płaszczyźnie kartki wzdłuż dowolnej prostej, wartości funkcji celu stale maleją lub stale rosną (w zależności od kierunku wędrówki po tej prostej) - to oczywiste: gdy idziemy prosto przed siebie po płaskim zboczu, zawsze idziemy pod górę lub w dół, czasem wzdłuż poziomicy, ale nie zmienia się monotoniczność przyjmowanych wartości. W szczególności gdy poruszamy się wzdłuż obwodu wielokąta, wartości rosną (gdy idziemy wzdłuż kolejnych boków) aż do największej możliwej, a potem maleją (gdy idziemy wzdłuż następnych boków) do najmniejszej możliwej (sprawdź to na swoim modelu). To dlatego ekstrema zawsze znajdujemy nad wierzchołkami wielokąta, nad którym rozpięta jest funkcja celu.
Zadanie 1. Rolnik Franciszek gospodaruje na 30 ha, na które składa się sześć jednakowych pól o powierzchni 5 ha każde. Franek może uprawiać na tych polach pszenicę i rzepak, przy czym na jednym polu może uprawiać tylko jedną roślinę. Pszenica daje plon w wysokości 7 ton z hektara, a rzepak 3 tony z hektara. Cena tony pszenicy wynosi 1000 zł, a cena tony rzepaku 2000 zł. Ile hektarów pola powinien obsiać Franciszek pszenicą a ile rzepakiem, aby zmaksymalizować swój przychód?
Zadanie 2. Fabryka wytwarza cztery rodzaje maszyn: tokarki, spawarki, giętarki i frezarki. Tygodniowo może wyprodukować 2 sztuki maszyn. Zysk z produkcji tokarki i giętarki to 10 000 zł za sztukę, spawarka przynosi zysk w wysokości 9 000 zł, a na frezarce fabryka zarabia 8 000 zł. Jeśli w tym samym tygodniu fabryka wyprodukuje dwie maszyny tego samego typu, to zysk z drugiej sztuki jest o 1000 zł mniejszy z powodu nadmiernej podaży maszyn tego typu na rynku. Jakie maszyny powinna produkować fabryka, aby zmaksymalizować swój tygodniowy zysk?
Zadanie 3. W firmie produkującej rowery oszacowano miesięczne koszty stałe (pensje, oświetlenie, czynsz itp.) na 9000 zł. Koszt wyprodukowania roweru to 1200 zł przy produkcji do 20 sztuk, a powyżej 20 sztuk jest o 100 zł mniejszy. Rower jest sprzedawany za 1500 zł. Jaka jest minimalna miesięczna produkcja zapewniająca tej firmie zysk?
Zadanie 1. Rolnik Franciszek gospodaruje na 30 ha, na których uprawia pszenicę i rzepak. Pszenica daje plon w wysokości 7 t/ha, a rzepak 3 t/ha. Cena tony pszenicy wynosi 1000 zł, a cena rzepaku 2000 zł. Franek ma podpisany kontrakt z lokalną wytwórnią margaryny na dostarczenie co najmniej 30 ton rzepaku. Ile hektarów pola powinien obsiać Franciszek pszenicą a ile rzepakiem, aby zmaksymalizować swój przychód?
Zadanie 2. W fabryce produkowane są dwa rodzaje rowerów: górskie i dziecięce. W ich produkcji wykorzystywane są cztery maszyny: tokarka, spawarka, giętarka i frezarka. Maszyny te mogą pracować przez określony czas, a potem ulegają awarii i należy je wymienić. Poniższa tabela przedstawia, czas pracy każdej z maszyn potrzebny na wyprodukowanie roweru każdego rodzaju.
| maszyna |
rower |
rower |
maksymalny czas |
| tokarka | 2 | 1 | 120 000 |
| spawarka | 1 | 3 | 90 000 |
| giętarka | 1 | 4 | 80 000 |
| frezarka | 2 | 0 | 60 000 |
Ile rowerów każdego typu powinna produkować fabryka, aby zmaksymalizować swój zysk, jeśli wiadomo, że rower górski przynosi 100 zł zysku, a rowerek dziecięcy 80 zł?
Zadanie 3. Firma produkuje karmę dla kotów będącą mieszanką mięsa baraniego i wieprzowego. Karma ta musi zawierać odpowiednią ilość białka i tłuszczu. W gotowej porcji karmy białka nie może być mniej niż 60 dag, a tłuszczu mniej niż 80 dag. W 1 kg baraniny znajduje się 10 dag białka i 40 dag tłuszczu. W 1 kg mięsa wieprzowego znajduje się 30 dag białka i 20 dag tłuszczu. Cena kilograma mięsa baraniego i wieprzowego to odpowiednio 30 zł i 20 zł. Ile należy kupić baraniny, a ile wieprzowiny, aby koszt zakupu mięsa do wyprodukowania porcji karmy dla kotów był minimalny?
Zadanie 1. Rolnik Franciszek gospodaruje na 30 ha, na których uprawia pszenicę i rzepak. Pszenica daje plon w wysokości 7 t/ha, a rzepak 3 t/ha. Cena tony pszenicy wynosi 1000 zł, a cena rzepaku 2000 zł. Franek ma podpisany kontrakt z lokalną wytwórnią margaryny na dostarczenie co najmniej 30 ton rzepaku. Pszenicy nie może wyprodukować więcej niż 105 ton ze względu na ograniczony popyt na to zboże. Ile hektarów pola powinien Franciszek obsiać pszenicą a ile rzepakiem, aby zmaksymalizować swój przychód?
Zadanie 2. Rozwiąż zadanie 2 dla GIM przy założeniu, że na podstawie kontraktów z odbiorcami fabryka jest zobowiązana do wyprodukowania co najmniej po 10 000 sztuk rowerów każdego rodzaju. Dodatkowo dla znalezionego rozwiązania liczby rowerów górskich i dziecięcych oblicz maksymalny zysk fabryki.
Zadanie 3. Do produkcji szamponu na porost włosów używa się dwóch ekstraktów: z pokrzywy i z krwawnika. Jeden litr ekstraktu z pokrzywy zawiera 2 g potasu i 1 g fosforu, a litr ekstraktu z krwawnika zawiera po 1 g potasu i fosforu. W gotowej porcji szamponu musi się znajdować co najmniej 40 g potasu i co najmniej 30 g fosforu. Cena ekstraktów z pokrzywy i z krwawnika w sprzedaży hurtowej wynosi 15 zł za litr. W jakiej ilości należy zakupić każdy z ekstraktów, aby koszt produkcji porcji szmponu był minimalny?
W styczniu punkty zdobyli:
- 3 pkt. - Maksymilian Grochowski SP 66 Warszawa, Joanna Lisiowska KSP Warszawa, Maja Metera SP 66 Warszawa, Tadeusz Niemiatowski SP 66 Warszawa, Katarzyna Piwowarska SP 66 Warszawa i Michał Popiel SP 6 Kłodzko,
- 2 pkt. - Aniela Czuma i Barbara Stajniak SP 66 Warszawa,
- 1,5 pkt. - Urszula Remisz SP 66 Warszawa,
- 0,5 pkt. - Dominika Prokocka SP 66 Warszawa.
Pozostałym uczestnikom nie przyznano punktów.
Po czterech miesiącach Ligi z wynikiem 12 pkt. prowadzi Joanna Lisiowska z KSP w Warszawie.
W styczniu punkty zdobyli:
- 3 pkt. - Daria Bumażnik GM 1 Jelenia Góra, Anna Łeń GM 1 Łódź i Barbara Piasecka GM 3 Oleśnica,
- 2,5 pkt. - Rafał Felczyński GM 2 Bolesławiec,
- 2,25 pkt. - Marek Mieniek GM 2 Bolesławiec,
- 2 pkt. - Krzysztof Bednarek GM 13 Wrocław, Mieszko Gałat GM 50 Bydgoszcz, Tomasz Kuśmierczyk GM 9 Wrocław, Aleksandra Polcyn GM Akademickie Toruń, Mateusz Rzepecki GM 14 Wrocław i Kacper Toczek GM 2 Wołów,
- 1 pkt. - Wiktor Baranowski GM 2 Bolesławiec, Justyna Witulska GM 3 Szprotawa.
Pozostałym uczestnikom nie przyznano punktów.
Po czterech miesiącach Ligi z wynikiem 11,25 pkt. prowadzi Anna Łeń z Gimnazjum nr 1 z Łodzi.
W styczniu punkty zdobyli:
- 3 pkt. - Adam Krasuski II LO Poznań,
- 2,5 pkt. - Łukasz Antczak ZST Włocławek, Krzysztof Danielak I LO Jelenia Góra i Tomasz Skalski III LO Wrocław,
- 2 pkt. - Bartłomiej Polcyn II LO Inowrocław.
Pozostałym uczestnikom nie przyznano punktów.
Po czterech miesiącach Ligi z wynikiem 10 pkt. prowadzi Tomasz Skalski z III LO z Wrocławia.
Zad. 1. Optymalnym rozwiązaniem dla Franciszka jest obsianie wszystkich sześciu pól pszenicą. Pszenica daje większy przychód z 1 ha uprawy niż rzepak, ponieważ 7·1000 = 7000 > 6000 = 3·2000.
Zad. 2. Fabryka powinna produkować jedną tokarkę i jedną giętarkę. Wtedy zarobi 20 000 zł. Produkcja uwzględniająca spawarkę lub frezarkę daje niższe zyski, a produkcja dwóch tokarek lub dwóch giętarek przyniesie fabryce 19 000 zł ze względu na nadmierną podaż.
Zad. 3. Minimalna produkcja zapewniająca zysk to 23 rowery. Przy produkcji 20 rowerów zysk wynosi 20·(1500-1200) = 6000 < 9000. Produkcja musi być zatem większa niż 20 rowerów, a dokładniej 9000/(1500-1100) = 22,5 rowera, czyli po zaokrągleniu do liczby całkowitej 23.
Zad. 1. Pszenica daje większy przychód z 1 ha niż rzepak, bo 7·1000 = 7000 > 6000 = 3·2000, więc to ona jest preferowaną uprawą. Jednak Franciszek jest zobowiązany kontraktem do dostarczenia co najmniej 30 ton rzepaku, dlatego musi wyprodukować 30 ton rzepaku na minimalnej powierzchni 10 ha, a pozostałe 20 ha powinien obsiać pszenicą. Wtedy jego przychód będzie maksymalny.
Zad. 2. Fabryka powinna produkować 30000 rowerów górskich i 12500 rowerów dziecięcych. Wtedy będzie miała maksymalny zysk.
Zad. 3. Koszt zakupu będzie najmniejszy gdy kupimy 1,2 kg baraniny i 1,6 kg wieprzowiny.
Zad. 1. Franciszek osiągnie maksymalny przychód, gdy obsieje 15 ha pszenicą i 15 ha rzepakiem.
Zad. 2. Dodatkowe ograniczenia nie wpłyną na rozwiązanie. Fabryka musi produkować 30 000 rowerów górskich i 12 500 rowerów dziecięcych. Wtedy zysk fabryki wyniesie 4 000 000 zł.
Zad. 3. Jest wiele rozwiązań, przy których koszt produkcji szamponu będzie minimalny. Na przykład, gdy do jego produkcji zużyjemy 10 l ekstraktu z pokrzywy i 20 l ekstraktu z krwawnika. Optymalne rozwiązania spełniają zależność p=30-k, gdzie k[tex]\in[/tex][0, 20], p to ilość ekstraktu z pokrzywy, a k - z krwawnika. Rozwiąznia te wypełniają w obszarze rozwiązań dopuszczalnych cały odcinek.
