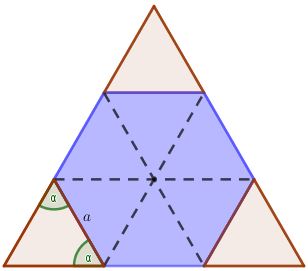
Zad. 1. W trójkąt równoboczny wpisano jest sześciokąt foremny jak na rysunku poniżej. Jaką część trójkąta stanowi ten sześciokąt?
Zad. 2. Koszt wynajęcia autokaru wynosi 36 zł za każdą rozpoczętą godzinę wynajmu i 1,80 zł za każdy przejechany kilometr. Ile kilometrów mogła mieć trasa wycieczki, jeśli za wynajęcie autokaru zapłacono 504 zł, a wycieczka trwała ponad 3 godziny, ale nie przekroczyła 6 godzin?
Zad. 3. Zastęp harcerski wyruszył na wędrówkę z miasta nad jezioro. Do pokonania mieli 12 km. Nad wodą harcerze wypoczęli, a potem tą samą trasą wrócili do miasta. Ścieżka, którą szli, biegła najpierw pod górę, później w dół, a potem po równinie. Pod górę zastęp szedł z prędkością 3 km/h, w dół – z prędkością 5 km/h, a po równinie 4 km/h. Przebycie drogi w obie strony zajęło im 6 i 4/15 godziny. Przez ile kilometrów ścieżka biegła po równinie?
W styczniu punkty zdobyli punkty zdobyli:
- 3 pkt. – Patryk Boruń SP 2 Wałbrzych, Adam Chowanek SP Mieroszów, Emilia Cichowska SP 14 Lubin, Natalia Cubala SP Jedlnia-Letnisko, Michał Dźwigaj SP 1 Przemków, Jakub Gospodarczyk SP Jedlnia Letnisko, Paulina Hołodniuk SP 2 Wołów, Filip Klich SP Ekola Wrocław, Zuzanna Lipka SP Jedlnia – Letnisko, Piotr Musielak SP 3 Ścinawa, Michał Plata SP 2 Syców, Kasjan Runke ZSP 2 Wałbrzych, Karol Skowera SP 2 Wałbrzych, Filip Timofiejczuk SP 3 Tarnowskie Góry, Michał Węgrzyn SP 9 Wrocław, Aleksandra Wiercińska SP Raszówka;
- 2,5 pkt. – Zuzanna Dropia SP Świerże Górne, Amelia Gugała SP Wrzosów, Weronika Kiniorska SP 65 Wrocław, Sandra Łuczak SP 107 Wrocław, Tobiasz Twardy SP Biedrzykowice;
- 2 pkt. – Jakub Binger SP Brzoza, Wojciech Domin SP Pisarzowice, Paweł Michałowski PrSP 1 Białystok, Agata Niemiec SP 28 Wałbrzych, Inga Niżańska SP 3 Wrocław, Tymoteusz Noremberg SP 29 Wrocław, Lena Nowacka SP 28 Wałbrzych, Julia Osowiec SP 3 Tarnowskie Góry, Karolina Prill SP Hańsko, Kacper Przywara SP Józefów n. Wisłą, Cezary Rębiś SP Jedlnia-Letnisko, Tymosz Srokosz SP 52 Warszawa, Szymon Wróbel SSP Gliwice;
- 1,5 pkt – Nataniel Jungowski SP ATUT Wrocław, Piotr Szymiec SP Pępowo;
- 1 pkt – Filip Godek SP 5 Kielce, Wiktoria Jaguszczak SP Grębocice, Maria Klasek SP 3 Tarnowskie Góry, Jakub Malicki SP Kobierzyce, Antoni Maracewicz SP Aslan Głogów, Anna Mędrzak SP 4 Warszawa.
Pozostali uczestnicy otrzymali poniżej 1 punktu
Zad. 1. Sześciokąt foremny o boku a możemy podzielić na sześć przystających trójkątów równobocznych o boku a (rysunek niżej). Ponieważ kąt wewnętrzny sześciokąta foremnego ma miarę 120°, jego kąty dopełniające przy boku a mają po 60° i stwierdzamy, że wszystkie trójkąty na rysunku są przystające. Zatem sześciokąt stanowi 6/9 = 2/3 trójkąta.
Zad. 2. Wycieczka trwała ponad 3 godziny, ale nie przekroczono 6 godzin, więc zapłacono za 4, 5 lub 6 godzin, czyli odpowiednio 144 zł, 180 zł lub 216 zł, a za przejechaną liczbę kilometrów 360 zł, 324 zł lub 288 zł. Trasa wycieczki mogła więc mieć 360:1,80 = 200 km, 324:1,80 = 180 km lub 288:1,80 = 160 km.
Zad. 3. Oznaczmy przez x długość drogi pod górę, przez y – długość drogi z góry, a przez a – długość drogi po równinie. W drodze powrotnej część drogi, która biegła pod górę, jest z góry i na odwrót. Długość drogi od miasta do jeziora wynosi x+y+a = 12. Czas trwania wędrówki w obie strony wynosi 64/15= 94/15 godziny. Na podstawie warunków zadania mamy x/3 + y/5 + a/4 + a/4 + y/3 + x/5 = 94/15. Rozwiązując układ równań, otrzymujemy po uproszczeniu x + y = 12 – a oraz 15a + 16(x+y) = 188, skąd a = 4. Zatem ścieżka biegła po równinie przez 4 km.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
