Podstawa programowa z matematyki dla klas 4-8 SP

Cele kształcenia – wymagania ogólne

I. Sprawność rachunkowa

• Wykonywanie nieskomplikowanych obliczeń w pamięci lub pisemnie w trudniejszych przykładach, wykorzystanie tych umiejętności w sytuacjach praktycznych. 
• Weryfikowanie i interpretowanie otrzymanych wyników oraz ocena sensowności rozwiązania. 

II. Wykorzystanie i tworzenie informacji

• Odczytywanie i interpretowanie danych przedstawionych w różnej formie oraz ich przetwarzanie. 
• Interpretowanie i tworzenie tekstów o charakterze matematycznym oraz graficzne przedstawianie danych. 
• Używanie języka matematycznego do opisu rozumowania i uzyskanych wyników. 

III. Wykorzystanie i interpretowanie reprezentacji

• Używanie prostych, dobrze znanych obiektów matematycznych, interpretowanie pojęć matematycznych i operowanie obiektami matematycznymi. 
• Dobieranie modelu matematycznego do prostej sytuacji oraz budowanie go w różnych kontekstach, także w kontekście praktycznym. 

IV. Rozumowanie i argumentacja

• Przeprowadzanie prostego rozumowania, podawanie argumentów uzasadniających poprawność rozumowania, rozróżnianie dowodu od przykładu. 
• Dostrzeganie regularności, podobieństw oraz analogii i formułowanie wniosków na ich podstawie. 
• Stosowanie strategii wynikającej z treści zadania, tworzenie strategii rozwiązania problemu, również w rozwiązaniach wieloetapowych oraz w takich, które wymagają umiejętności łączenia wiedzy z różnych działów matematyki.  

Treści nauczania – wymagania szczegółowe

KLASY IV–VI 

1. Liczby naturalne w dziesiątkowym układzie pozycyjnym

uczeń:

• zapisuje i odczytuje liczby wielocyfrowe,
• interpretuje liczby na osi liczbowej,
• porównuje i zaokrągla liczby,
• liczby w zakresie do 3 000 zapisane w systemie rzymskim przedstawia w systemie dziesiątkowym, a zapisane w systemie dziesiątkowym przedstawia w systemie rzymskim.

2. Działania na liczbach naturalnych
uczeń:

• dodaje i odejmuje w pamięci liczby naturalne dwucyfrowe lub większe, liczbę jednocyfrową dodaje do dowolnej liczby naturalnej i odejmuje od dowolnej liczby naturalnej,
• dodaje i odejmuje liczby naturalne wielocyfrowe sposobem pisemnym i za pomocą kalkulatora, 
• mnoży i dzieli liczbę naturalną przez liczbę naturalną jednocyfrową, dwucyfrową lub trzycyfrową sposobem pisemnym, w pamięci (w najprostszych przykładach) i za pomocą kalkulatora (w trudniejszych przykładach),
• wykonuje dzielenie z resztą liczb naturalnych, 
• stosuje wygodne sposoby ułatwiające obliczenia, w tym przemienność lub łączność dodawania i mnożenia oraz rozdzielność mnożenia względem dodawania, 
• porównuje liczby naturalne z wykorzystaniem ich różnicy lub ilorazu, 
• rozpoznaje liczby podzielne przez 2, 3, 4, 5, 9, 10, 100, 
• rozpoznaje liczbę złożoną, gdy jest ona jednocyfrowa lub dwucyfrowa, a także gdy na istnienie dzielnika właściwego wskazuje cecha podzielności,
• rozkłada liczby dwucyfrowe na czynniki pierwsze, 
• oblicza kwadraty i sześciany liczb naturalnych,
• stosuje reguły dotyczące kolejności wykonywania działań,
• szacuje wyniki działań,
• znajduje największy wspólny dzielnik w sytuacjach nie trudniejszych niż NWD(600, 72), NWD(140, 567), NWD(10000, 48), NWD(910, 2016) oraz wyznacza najmniejszą wspólną wielokrotność dwóch liczb naturalnych metodą rozkładu na czynniki,
• rozpoznaje wielokrotności danej liczby, kwadraty, sześciany, liczby pierwsze, liczby złożone, 
• odpowiada na pytania dotyczące liczebności zbiorów różnych rodzajów liczb wśród liczb z pewnego niewielkiego zakresu (np. od 1 do 200 czy od 100 do 1000), o ile liczba w odpowiedzi jest na tyle mała, że wszystkie rozważane liczby uczeń może wypisać, 
• rozkłada liczby naturalne na czynniki pierwsze, w przypadku gdy co najwyżej jeden z tych czynników jest liczbą większą niż 10,
• wyznacza wynik dzielenia z resztą liczby a przez liczbę b i zapisuje liczbę a w postac: a = b ^. q + r 

3. Liczby całkowite
uczeń:

• podaje praktyczne przykłady stosowania liczb ujemnych,
• interpretuje liczby całkowite na osi liczbowej,
• oblicza wartość bezwzględną,
• porównuje liczby całkowite,
• wykonuje proste rachunki pamięciowe na liczbach całkowitych. 

4. Ułamki zwykłe i dziesiętne
uczeń:

• opisuje część danej całości za pomocą ułamka,
• przedstawia ułamek jako iloraz liczb naturalnych, a iloraz liczb naturalnych jako ułamek zwykły, 
• skraca i rozszerza ułamki zwykłe,
• sprowadza ułamki zwykłe do wspólnego mianownika,
• przedstawia ułamki niewłaściwe w postaci liczby mieszanej, a liczbę mieszaną w postaci ułamka niewłaściwego, 
• zapisuje wyrażenia dwumianowane w postaci ułamka dziesiętnego i odwrotnie, 
• zaznacza i odczytuje ułamki zwykłe i dziesiętne na osi liczbowej oraz odczytuje ułamki zwykłe i dziesiętne zaznaczone na osi liczbowej,
• zapisuje ułamki dziesiętne skończone w postaci ułamków zwykłych, 
• zamienia ułamki zwykłe o mianownikach będących dzielnikami liczb 10, 100, 1000 itd. na ułamki dziesiętne skończone dowolną metodą (przez rozszerzanie lub skracanie ułamków zwykłych, dzielenie licznika przez mianownik w pamięci, pisemnie lub za pomocą kalkulatora),
• zapisuje ułamki zwykłe o mianownikach innych niż wymienione w pkt 9 w postaci rozwinięcia dziesiętnego nieskończonego (z użyciem wielokropka po ostatniej cyfrze), uzyskane w wyniku dzielenia licznika przez mianownik w pamięci, pisemnie lub za pomocą kalkulatora, 
• zaokrągla ułamki dziesiętne, 
• porównuje ułamki (zwykłe i dziesiętne), 
• oblicza liczbę, której część jest podana (wyznacza całość, z której określono część za pomocą ułamka), 
• wyznacza liczbę, która powstaje po powiększeniu lub pomniejszeniu o pewną część innej liczby, 

5. Działania na ułamkach zwykłych i dziesiętnych
uczeń:

• dodaje, odejmuje, mnoży i dzieli ułamki zwykłe o mianownikach jedno- lub dwucyfrowych, a także liczby mieszane, 
• dodaje, odejmuje, mnoży i dzieli ułamki dziesiętne w pamięci (w przykładach najprostszych), pisemnie i za pomocą kalkulatora (w przykładach trudnych),
• wykonuje nieskomplikowane rachunki, w których występują jednocześnie ułamki zwykłe i dziesiętne, 
• porównuje ułamki z wykorzystaniem ich różnicy,
• oblicza ułamek danej liczby całkowitej, 
• oblicza kwadraty i sześciany ułamków zwykłych i dziesiętnych oraz liczb mieszanych,
• oblicza wartość prostych wyrażeń arytmetycznych, stosując reguły dotyczące kolejności wykonywania działań, wykonuje działania na ułamkach dziesiętnych, używając własnych, poprawnych strategii lub za pomocą kalkulatora,
• oblicza wartości wyrażeń arytmetycznych, wymagających stosowania działań arytmetycznych na liczbach całkowitych lub liczbach zapisanych za pomocą ułamków zwykłych, liczb mieszanych i ułamków dziesiętnych, także wymiernych ujemnych o stopniu trudności nie większym niż:
   -¹/₂ : 0,25 + 5,25 : 0,05 – 7¹/₂ · (2,5 – 3²/₃) + 1,25,

6. Elementy algebry
uczeń:

• korzysta z nieskomplikowanych wzorów, w których występują oznaczenia literowe, opisuje wzór słowami; [tex]\frac{x-2}{3}\ = 4[/tex] ,
• stosuje oznaczenia literowe nieznanych wielkości liczbowych i zapisuje proste wyrażenia algebraiczne na podstawie informacji osadzonych w kontekście praktycznym, na przykład zapisuje obwód trójkąta o bokach: a, a+2, b, rozwiązuje równania pierwszego stopnia z jedną niewiadomą występującą po jednej stronie równania (przez zgadywanie, dopełnianie lub wykonanie działania odwrotnego), na przykład [tex]\frac{x-2}{3}\ = 4[/tex]. 

7. Proste i odcinki
uczeń:

• rozpoznaje i nazywa figury: punkt, prosta, półprosta, odcinek,
• rozpoznaje proste i odcinki prostopadłe i równoległe, na przykład jak w sytuacji określonej w zadaniu: Odcinki AB i CD są prostopadłe, odcinki CD i EF są równoległe oraz odcinki EF
  i DF są prostopadłe. Określ wzajemne położenie odcinków DF oraz AB. Wykonaj odpowiedni rysunek, 
• rysuje pary odcinków prostopadłych i równoległych,
• mierzy odcinek z dokładnością do 1 mm,
• znajduje odległość punktu od prostej. 

8. Kąty
uczeń:

• wskazuje w dowolnym kącie ramiona i wierzchołek,
• mierzy z dokładnością do 10 st kąty mniejsze niż 180 st,
• rysuje kąty mniejsze od 180 st,
• rozpoznaje kąt prosty, ostry i rozwarty,
• porównuje kąty,
• rozpoznaje kąty wierzchołkowe i przyległe oraz korzysta z ich własności.

9. Wielokąty, koła i okręgi
uczeń:

• rozpoznaje i nazywa trójkąty ostrokątne, prostokątne, rozwartokątne, równoboczne i równoramienne; 
• konstruuje trójkąt o danych trzech bokach i ustala możliwość zbudowania trójkąta na podstawie nierówności trójkąta,
• stosuje twierdzenie o sumie kątów wewnętrznych trójkąta,
• rozpoznaje i nazywa: kwadrat, prostokąt, romb, równoległobok i trapez,
• zna najważniejsze własności kwadratu, prostokąta, rombu, równoległoboku i trapezu, rozpoznaje figury osiowosymetryczne i wskazuje osie symetrii figur, 
• wskazuje na rysunku cięciwę, średnicę oraz promień koła i okręgu,
• rysuje cięciwę koła i okręgu, a także, jeżeli dany jest środek okręgu - promień i średnicę; 
• w trójkącie równoramiennym wyznacza przy danym jednym kącie miary pozostałych kątów oraz przy danych obwodzie i długości jednego boku - długości pozostałych boków.

10. Bryły
uczeń: 

• rozpoznaje graniastosłupy proste, ostrosłupy, walce, stożki i kule w sytuacjach praktycznych i wskazuje te bryły wśród innych modeli brył, 
• wskazuje wśród graniastosłupów prostopadłościany i sześciany i uzasadnia swój wybór,
• rozpoznaje siatki graniastosłupów prostych i ostrosłupów,
• rysuje siatki prostopadłościanów,
• wykorzystuje podane zależności między długościami krawędzi graniastosłupa do wyznaczania długości poszczególnych krawędzi. 

11. Obliczenia w geometrii
uczeń:

• oblicza obwód wielokąta o danych długościach boków,
• oblicza pola: trójkąta, kwadratu, prostokąta, rombu, równoległoboku, trapezu, przedstawionych na rysunku oraz w sytuacjach praktycznych, w tym także dla danych wymagających zamiany jednostek i w sytuacjach z nietypowymi wymiarami, na przykład pole trójkąta o boku 1 km i wysokości 1 mm, 
• stosuje jednostki pola: mm², cm², dm², m², km², ar, hektar (bez zamiany jednostek w trakcie obliczeń), 
• oblicza pola wielokątów metodą podziału na mniejsze wielokąty lub uzupełniania do większych wielokątów jak w sytuacjach:
   
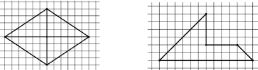
• oblicza objętość i pole powierzchni prostopadłościanu przy danych długościach krawędzi,
• stosuje jednostki objętości i pojemności: mililitr, litr, cm³, dm³, m³, 
• oblicza miary kątów, stosując przy tym poznane własności kątów i wielokątów. 

12. Obliczenia praktyczne
uczeń:

• interpretuje 100% danej wielkości jako całość, 50% – jako połowę, 25% – jako jedną czwartą, 10% – jako jedną dziesiątą, 1% – jako jedną setną części danej wielkości liczbowej,
• w przypadkach osadzonych w kontekście praktycznym oblicza procent danej wielkości w stopniu trudności typu 50%, 20%, 10%,
• wykonuje proste obliczenia zegarowe na godzinach, minutach i sekundach,
• wykonuje proste obliczenia kalendarzowe na dniach, tygodniach, miesiącach, latach,
• odczytuje temperaturę (dodatnią i ujemną),
• zamienia i prawidłowo stosuje jednostki długości: milimetr, centymetr, decymetr, metr, kilometr, 
• zamienia i prawidłowo stosuje jednostki masy: gram, dekagram, kilogram, tona, 
• oblicza rzeczywistą długość odcinka, gdy dana jest jego długość w skali oraz długość odcinka w skali, gdy dana jest jego rzeczywista długość,
• w sytuacji praktycznej oblicza: drogę przy danej prędkości i czasie, prędkość przy danej drodze i czasie, czas przy danej drodze i prędkości oraz stosuje jednostki prędkości km/h i m/s.

13. Elementy statystyki opisowej
uczeń:

• gromadzi i porządkuje dane, 
• odczytuje i interpretuje dane przedstawione w tekstach, tabelach, na diagramach i na wykresach, na przykład: wartości z wykresu, wartość największą, najmniejszą, opisuje przedstawione w tekstach, tabelach, na diagramach i na wykresach zjawiska przez określenie przebiegu zmiany wartości danych, na przykład z użyciem określenia „wartości rosną”, „wartości maleją”, „wartości są takie same” („przyjmowana wartość jest stała”).

14. Zadania tekstowe
uczeń:

• czyta ze zrozumieniem tekst zawierający informacje liczbowe, 
• wykonuje wstępne czynności ułatwiające rozwiązanie zadania, w tym rysunek pomocniczy lub wygodne dla niego zapisanie informacji i danych z treści zadania, 
• dostrzega zależności między podanymi informacjami,
• dzieli rozwiązanie zadania na etapy, stosując własne, poprawne, wygodne dla niego strategie rozwiązania,
• do rozwiązywania zadań osadzonych w kontekście praktycznym stosuje poznaną wiedzę z zakresu arytmetyki i geometrii oraz nabyte umiejętności rachunkowe, a także własne poprawne metody,
• weryfikuje wynik zadania tekstowego, oceniając sensowność rozwiązania np. poprzez szacowanie, sprawdzanie wszystkich warunków zadania, ocenianie rzędu wielkości otrzymanego wyniku,
• układa zadania i łamigłówki, rozwiązuje je; stawia nowe pytania związane z sytuacją w rozwiązanym zadaniu

 klasy VII-VIII

1. Potęgi o podstawach wymiernych.
Uczeń:

• zapisuje iloczyn jednakowych czynników w postaci potęgi o wykładniku, całkowitym dodatnim, 
• mnoży i dzieli potęgi o wykładnikach całkowitych dodatnich,
• mnoży potęgi o różnych podstawach i jednakowych wykładnikach, 
• podnosi potęgę do potęgi, 
• odczytuje i zapisuje liczby w notacji wykładniczej a ∙ 10^k, gdy 1 ≤ a < 10, k jest liczbą całkowitą.

2. Pierwiastki.
Uczeń:

• oblicza wartości pierwiastków kwadratowych i sześciennych z liczb, które są odpowiednio kwadratami lub sześcianami liczb wymiernych,
• szacuje wielkość danego pierwiastka kwadratowego lub sześciennego oraz wyrażenia arytmetycznego zawierającego pierwiastki,
• porównuje wartość wyrażenia arytmetycznego zawierającego pierwiastki z daną liczbą wymierną oraz znajduje liczby wymierne większe lub mniejsze od takiej wartości, na przykład znajduje liczbę całkowitą a taką, że: a ≤[tex]\sqrt{137}[/tex] < a + 1, 
• oblicza pierwiastek z iloczynu i ilorazu dwóch liczb, wyłącza liczbę przed znak pierwiastka i włącza liczbę pod znak pierwiastka, 
• mnoży i dzieli pierwiastki tego samego stopnia.

3. Tworzenie wyrażeń algebraicznych z jedną i z wieoma zmiennymi.
Uczeń:

• zapisuje wyniki podanych działań w postaci wyrażeń algebraicznych jednej lub kilku zmiennych,
• oblicza wartości liczbowe wyrażeń algebraicznych,
• zapisuje zależności przedstawione w zadaniach w postaci wyrażeń algebraicznych jednej lub kilku zmiennych, 
• zapisuje rozwiązania zadań w postaci wyrażeń algebraicznych jak w przykładzie:
  Bartek i Grześ zbierali kasztany. Bartek zebrał n kasztanów, Grześ zebrał 7 razy więcej. Następnie Grześ w drodze do domu zgubił 10 kasztanów, a połowę pozostałych oddał Bartkowi. Ile kasztanów ma teraz Bartek, a ile ma Grześ?

4. Przekształcanie wyrażeń algebraicznych. Sumy algebraiczne i działania na nich.
Uczeń:

• porządkuje jednomiany i dodaje jednomiany podobne (tzn. różniące się jedynie
  współczynnikiem liczbowym), 
• dodaje i odejmuje sumy algebraiczne, dokonując przy tym redukcji wyrazów podobnych,
• mnoży sumy algebraiczne przez jednomian i dodaje wyrażenia powstałe z mnożenia sum algebraicznych przez jednomiany, 
• mnoży dwumian przez dwumian, dokonując redukcji wyrazów podobnych.

 5. Obliczenia procentowe.
Uczeń:

• przedstawia część wielkości jako procent tej wielkości, 
• oblicza liczbę a równą p procent danej liczby b, 
• oblicza, jaki procent danej liczby b stanowi liczba a, 
• oblicza liczbę b, której p procent jest równe a,
• stosuje obliczenia procentowe do rozwiązywania problemów w kontekściepraktycznym, również w przypadkach wielokrotnych podwyżek lub obniżek danej wielkości.

6. Równania z jedną niewiadomą.
Uczeń:

• sprawdza, czy dana liczba jest rozwiązaniem równania (stopnia pierwszego, drugiego lub trzeciego) z jedną niewiadomą, na przykład sprawdza, które liczby całkowite niedodatnie i większe od –8 są rozwiązaniami równania [tex]\frac{x^3}{8} + \frac{x^2}{2}\ = 0[/tex], 
• rozwiązuje równania pierwszego stopnia z jedną niewiadomą metodą równań
  równoważnych,
• rozwiązuje równania, które po prostych przekształceniach wyrażeń algebraicznych sprowadzają się do równań pierwszego stopnia z jedną niewiadomą,
• rozwiązuje zadania tekstowe za pomocą równań pierwszego stopnia z jedną niewiadomą, w tym także z obliczeniami procentowymi,
• przekształca proste wzory, aby wyznaczyć zadaną wielkość we wzorach geometrycznych (np. pól figur) i fizycznych (np. dotyczących prędkości, drogi i czasu).

7. Proporcjonalność prosta.
Uczeń:

• podaje przykłady wielkości wprost proporcjonalnych,
• wyznacza wartość przyjmowaną przez wielkość wprost proporcjonalną w przypadku konkretnej zależności proporcjonalnej, na przykład wartość zakupionego towaru w zależności od liczby sztuk towaru, ilość zużytego paliwa w zależności od liczby przejechanych kilometrów, liczby przeczytanych stron książki w zależności od czasu jej czytania,
• stosuje podział proporcjonalny.

8. Własności figur geometrycznych na płaszczyźnie.
Uczeń:

• zna i stosuje twierdzenie o równości kątów wierzchołkowych (z wykorzystaniem zależności między kątami przyległymi), 
• pzedstawia na płaszczyźnie dwie proste w różnych położeniach względem siebie, w szczególności proste prostopadłe i proste równoległe,  
• korzysta z własności prostych równoległych, w szczególności stosuje równość kątów odpowiadających i naprzemianległych, zna i stosuje cechy przystawani  trójkątów, 
• zna i stosuje własności trójkątów równoramiennych (równość kątów przy podstawie),  zna nierówność trójkąta AB + BC ≥ AC i wie, kiedy zachodzi równość, 
• wykonuje proste obliczenia geometryczne wykorzystując sumę kątów wewnętrznych trójkąta i własności trójkątów równoramiennych, 
• zna i stosuje w sytuacjach praktycznych twierdzenie Pitagorasa (bez twierdzenia odwrotnego),
• przeprowadza dowody geometryczne o poziomie trudności nie większym niż w przykładach:
  Dany jest ostrokątny trójkąt równoramienny ABC, w którym AC=BC. W tym trójkącie poprowadzono wysokość AD. Udowodnij, że kąt ABC jest dwa razy większy od kąta BAD, na bokach BC i CD prostokąta ABCD zbudowano, na zewnątrz prostokąta, dwa trójkąty równoboczne BCE i CDF. Udowodnij, że AE = AF.

9. Wielokąty. Uczeń:

• zna pojęcie wielokąta foremnego,
• stosuje wzory na pole trójkąta, prostokąta, kwadratu, równoległoboku, rombu,trapezu, a także do wyznaczania długości odcinków o poziomie trudności nie większym niż w przykładach:
  a) oblicz najkrótszą wysokość trójkąta prostokątnego o bokach długości: 5 cm, 12 cm i 13 cm,
  b) Przekątne rombu ABCD mają długości AC = 8 d m i BD = 10 dm.
  Przekątną BD rombu przedłużono do punktu E w taki sposób, że odcinek BE jest dwa razy dłuższy od tej przekątnej. Oblicz pole trójkąta CDE. (zadanie ma dwie odpowiedzi).

10. Oś liczbowa. Układ współrzędnych na płaszczyźnie.
Uczeń:

• zaznacza na osi liczbowej zbiory liczb spełniających warunek taki jak lub
  taki jak x ≥ 1,5 lub takich jak x < -⁴/₇, 
• znajduje współrzędne danych (na rysunku) punktów kratowych w układzie współrzędnych na płaszczyźnie, 
• rysuje w układzie współrzędnych na płaszczyźnie punkty kratowe o danych współrzędnych całkowitych (dowolnego znaku), 
• znajduje środek odcinka, którego końce mają dane współrzędne (całkowite lub wymierne) oraz znajduje współrzędne drugiego końca odcinka, gdy dany  jeden koniec i środek,
• oblicza długość odcinka, którego końce są danymi punktami kratowymi w układzie współrzędnych, 
• dla danych punktów kratowych A i B znajduje inne punkty kratowe należące do prostej AB.

11. Geometria przestrzenna.
Uczeń: 

• rozpoznaje graniastosłupy i ostrosłupy – w tym proste i prawidłowe,
• oblicza objętości i pola powierzchni graniastosłupów prostych, prawidłowych i takich, które nie są prawidłowe o poziomie trudności nie większym niż w przykładowym zadaniu:
  Podstawą graniastosłupa prostego jest trójkąt równoramienny, którego dwa równe kąty mają po 45⁰, a najdłuższy bok ma długość 6 [tex]\sqrt{2}[/tex] dm. Jeden z boków prostokąta, który jest w tym graniastosłupie ścianą boczną o największej powierzchni, ma długość 4 dm. Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa, 
• oblicza objętości i pola powierzchni ostrosłupów prawidłowych i takich, które nie są prawidłowe o poziomie trudności nie większym niż w przykładzie:
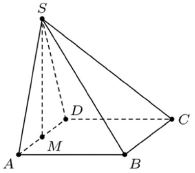
  Prostokąt ABCD jest podstawą ostrosłupa ABCDS, punkt M jest środkiem krawędzi AD, odcinek MS jest wysokością ostrosłupa. Dane są następujące długości krawędzi: AD =10 cm, AS = 13 cm oraz AB = 20 cm. Oblicz objętość ostrosłupa.

12. Wprowadzenie do kombinatoryki i rachunku prawdopodobieństwa. Uczeń:

• wyznacza zbiory obiektów, analizuje i oblicza, ile jest obiektów, mających daną własność, w przypadkach niewymagających stosowania reguł mnożenia i dodawania,
• przeprowadza proste doświadczenia losowe, polegające na rzucie monetą, rzucie sześcienną kostką do gry, rzucie kostką wielościenną lub losowaniu kuli spośród zestawu kul, analizuje je i oblicza prawdopodobieństwa zdarzeń w doświadczeniach losowych.

13. Odczytywanie danych i elementy statystyki opisowej. Uczeń:

• interpretuje dane przedstawione za pomocą tabel, diagramów słupkowych i kołowych, wykresów, w tym także wykresów w układzie współrzędnych,
• tworzy diagramy słupkowe i kołowe oraz wykresy liniowe na podstawie zebranych przez siebie danych lub danych pochodzących z różnych źródeł, 
• oblicza średnią arytmetyczną kilku liczb. 

14. Długość okręgu i pole koła.
Uczeń:

• oblicza długość okręgu o danym promieniu lub danej średnicy,
• oblicza promień lub średnicę okręgu o danej długości okręgu, 
• oblicza pole koła o danym promieniu lub danej średnicy, 
• oblicza promień lub średnicę koła o danym polu koła, 
• oblicza pole pierścienia kołowego o danych promieniach lub średnicach  obu okręgów tworzących pierścień.

15. Symetrie.
Uczeń:

• rozpoznaje symetralną odcinka i dwusieczną kąta, 
• zna i stosuje w zadaniach podstawowe własności symetralnej odcinka i dwusiecznej kąta jak w przykładowym zadaniu:
  Wierzchołek C rombu ABCD leży na symetralnych boków AB i AD. Oblicz kąty tego rombu, 
• rozpoznaje figury osiowosymetryczne i wskazuje ich osie symetrii oraz uzupełnia figurę do figury osiowosymetrycznej przy danych: osi symetrii figury i części figury, 
• rozpoznaje figury środkowosymetryczne i wskazuje ich środki symetrii.

16. Zaawansowane metody zliczania.
Uczeń:

• stosuje regułę mnożenia do zliczania par elementów o określonych własnościach, 
• stosuje regułę dodawania i mnożenia do zliczania par elementów w sytuacjach, wymagających rozważenia kilku przypadków, na przykład w zliczaniu liczb naturalnych trzycyfrowych podzielnych przez 5 i mających trzy różne cyfry albo jak w zadaniu:
  W klasie jest 14 dziewczynek i 11 chłopców. Na ile sposobów można z tej klasy wybrać dwuosobową delegację składającą się z jednej dziewczynki i jednego chłopca?

17. Rachunek prawdopodobieństwa.
Uczeń:

• oblicza prawdopodobieństwa zdarzeń w doświadczeniach, polegających na rzucie dwiema kostkami lub losowaniu dwóch elementów ze zwracaniem, 
• oblicza prawdopodobieństwa zdarzeń w doświadczeniach, polegających na losowaniu dwóch elementów bez zwracania jak w przykładzie:
  Z urny zawierającej kule ponumerowane liczbami od 1 do 7 losujemy bez zwracania dwie kule. Oblicz prawdopodobieństwo tego, że suma liczb na wylosowanych kulach będzie parzysta.

Warunki i sposób realizacji

Proponuje się, aby w latach 2017/18, 2018/19 i 2019/20 w klasie VII zrealizowano dodatkowo niektóre działy podstawy programowej dla klas IV–VI, o ile nie zostały one wcześniej zrealizowane w klasach IV–VI, gdzie
uczeń:

• liczby w zakresie do 3 000 zapisane w systemie rzymskim przedstawia w systemie dziesiątkowym, a zapisane w systemie dziesiątkowym przedstawia w systemie rzymskim.
• znajduje największy wspólny dzielnik w sytuacjach nie trudniejszych niż NWD(600, 72), NWD(140, 567), NWD(10000, 48), NWD(910, 2016) oraz wyznacza najmniejszą wspólną wielokrotność dwóch liczb naturalnych metodą rozkładu na czynniki, 
• rozpoznaje wielokrotności danej liczby, kwadraty, sześciany, liczby pierwsze, liczby złożone,
  odpowiada na pytania dotyczące liczebności zbiorów różnych rodzajów liczb wśród liczb z pewnego niewielkiego zakresu (np. od 1 do 200 czy od 100 do 1000), o ile liczba w odpowiedzi jest na tyle mała, że wszystkie rozważane liczby uczeń może wypisać,  
• rozkłada liczby naturalne na czynniki pierwsze, w przypadku gdy co najwyżej jeden z tych czynników jest liczbą większą niż 10,
  wyznacza wynik dzielenia z resztą liczby a przez liczbę b i zapisuje liczbę a w postac: a = b . q + r  
• oblicza liczbę, której część jest podana (wyznacza całość, z której określono część za pomocą ułamka), 
• wyznacza liczbę, która powstaje po powiększeniu lub pomniejszeniu o pewną część innej liczby, 
• wykonuje działania na ułamkach dziesiętnych, używając własnych, poprawnychstrategii lub za pomocą kalkulatora,
• w trójkącie równoramiennym wyznacza przy danym jednym kącie miary pozostałych kątów oraz przy danych obwodzie i długości jednego boku długości pozostałych boków,
• wykorzystuje podane zależności między długościami krawędzi graniastosłupa do wyznaczania długości poszczególnych krawędzi,
• oblicza pola wielokątów metodą podziału na mniejsze wielokąty lub uzupełniania do większych wielokątów.

Działy: długość okręgu i pole koła, symetrie, zaawansowane metody zliczania, rachunek prawdopodobieństwa podstawy programowej dla klas VII i VIII mogą zostać zrealizowane po egzaminie ósmoklasisty.

W klasach IV–VI, kiedy nauka matematyki odbywa się przede wszystkim na konkretnych obiektach, należy przede wszystkim zadbać o pracę na przykładach, bez wprowadzania
nadmiaru pojęć abstrakcyjnych. Dużą pomocą dla ucznia jest możliwość eksperymentowania z liczbami, rozwiązywania zagadek logicznych i logiczno matematycznych, a także ćwiczenia polegające na pracy lub zabawie z różnymi figurami lub bryłami w geometrii. W szczególności, rozwiązywanie równań przez zgadywanie powinno być w klasach IV–VI traktowane jako poprawna metoda.

W klasach IV–VI zaleca się szczególną ostrożność przy wymaganiu od ucznia ścisłości języka matematycznego. Należy dbać o precyzję wypowiedzi, ale trzeba pamiętać o tym, aby unikać sytuacji, w której uczeń zostaje uznany za nieuzdolnionego matematycznie, gdy nie potrafi wyrazić poprawnego rozwiązania w sposób odpowiednio formalny, zgodnie z oczekiwaniami nauczyciela. Umiejętność posługiwania się takimi pojęciami matematycznymi jak: kąt, długość, pole, suma algebraiczna jest o wiele bardziej istotna niż zapamiętanie formalnej definicji. W nauczaniu matematyki istotne jest, aby uczeń zrozumiał
sens reguł formalnych.

Większość uczniów w praktyce korzysta z kalkulatorów bądź innych urządzeń
elektronicznych. Niemniej umiejętność wykonywania rachunków w pamięci, a także pisemnie, jest istotna. Obliczenia pamięciowe, w tym szacowanie wyników, bardzo przydają się w życiu codziennym. Samodzielne wykonywanie obliczeń, zarówno pamięciowych jak i pisemnych, daje uczniom o wiele lepsze wyobrażenie o liczbach i ich wielkościach, niż prowadzenie rachunków za pomocą sprzętu elektronicznego.

Myślenie abstrakcyjne kształtuje się w wieku 11–15 lat, ale u wielu dzieci w różnym tempie,
nie musi to oznaczać większych bądź mniejszych zdolności matematycznych. Z uwagi na różną szybkość rozwoju myślenia uczniów klas VII i VIII, a także, częściowo klasy VI,można rozważyć wprowadzenie nauczania matematyki w grupach międzyoddziałowych na różnych poziomach, podobnie jak to jest praktykowane w nauczaniu języków obcych nowożytnych. Grupy międzyoddziałowe realizowałyby różne partie materiału w tempie dostosowanym do możliwości uczniów, przy zachowaniu realizacji podstawy programowej.Takie podejście nie powinno dzielić uczniów na lepszych lub gorszych, ale ma umożliwić uczniom, u których myślenie abstrakcyjne rozwija się wolniej, płynne przejście do etapu myślenia abstrakcyjnego. Uczniom, u których to myślenie rozwinęło się szybciej, należy proponować zadania trudniejsze i pozwalające na głębszą analizę zagadnień, aby właściwie stymulować ich rozwój.

Zadania na dowodzenie stanowią ważny element wykształcenia matematycznego. Uczeń powinien dowiedzieć się, że w twierdzeniach zaczynających się od słów „wykaż, że dla każdego…” podawanie wielu przykładów nie jest dowodem, a podanie jednego kontrprzykładu świadczy o tym, że stwierdzenie nie jest prawdziwe. Nie oznacza to, że uczeń nie powinien szukać przykładów bądź kontrprzykładów. Często takie poszukiwanie i sprawdzanie prawdziwości tezy dla konkretnych przypadków pozwala uczniowi zrozumieć postawiony problem, a następnie podać ogólne rozumowanie.

W szkole podstawowej zadania na dowodzenie powinny być proste (w przypadku zdolnych
uczniów można rozszerzyć stopień trudności). Oznacza to, że na przykład do dowodu zadania z geometrii powinno wystarczyć obliczanie kątów (z wykorzystaniem równości kątów wierzchołkowych, odpowiadających i naprzemianległych, twierdzenia o sumie kątów trójkąta
oraz twierdzenia o kątach przy podstawie trójkąta równoramiennego), użycie cech przystawania trójkątów do uzasadnienia przystawania jednej dostrzeżonej pary trójkątów przystających oraz wyciągnięcie wniosków z tej własności.

Wprowadzenie do rachunku prawdopodobieństwa należy poprzedzić zadaniami, w których uczniowie wykonują doświadczenia, na przykład wielokrotne rzuty kostką. Można wówczas wskazać związek pomiędzy częstością zdarzenia a jego prawdopodobieństwem.

Szczególną rolę w kształceniu matematycznym odgrywają zadania ze statystyki. Z jednej strony odczytywanie i prezentowanie danych, wiąże matematykę z życiem codziennym i otwiera cały wachlarz zastosowań praktycznych. Wskazane jest, aby znaczna część zadań dotyczyła danych rzeczywistych wraz z podaniem ich weryfikowalnego źródła. Z drugiej strony, na przykład operowanie wykresami zależności pozwala na intuicyjne opanowanie trudnych i abstrakcyjnych pojęć takich jak funkcja, monotoniczność, ekstrema, przy użyciu minimalnej wiedzy matematycznej (nie należy wprowadzać tych pojęć w szkole podstawowej). Stanowi to wstęp do wprowadzenia tych pojęć w szkole ponadpodstawowej. Dla przykładu załączono kilka zadań ze statystyki, z których część może być wykorzystana na zajęciach, bądź w projektach edukacyjnych uczniowskich. 

1. We wszystkich trzech klasach VI w pewnej szkole przeprowadzono ankietę „Jaki smak lodów lubisz najbardziej?”. W ankiecie wzięli udział wszyscy uczniowie z tych klas. Wyniki, jakie otrzymano, były następujące: w klasie VIa – 12 osób wybrało lody czekoladowe, 7 osób – lody waniliowe, a 6 osób – lody truskawkowe. W klasie VIb – 5 osób wybrało lody waniliowe, 10 osób – lody truskawkowe, a 6 osób – lody czekoladowe. W ostatniej klasie VIc po 7 osób wybrało lody truskawkowe i lody czekoladowe, a 9 osób lody waniliowe. Wykonaj diagram słupkowy przedstawiający wyniki tej ankiety. Odczytaj, które lody cieszą się największą popularnością w klasach VI w tej szkole. 
2. Odczytaj z prognozy pogody (podanej w formie meteorogramu), w którym z najbliższych dni prognozowana temperatura będzie największa. Podaj, w jakich godzinach, według prognozy, temperatura powietrza będzie rosła, a w jakich malała. W którym z najbliższych dni pogoda będzie najlepsza do organizacji wycieczki?Odpowiedź uzasadnij. 
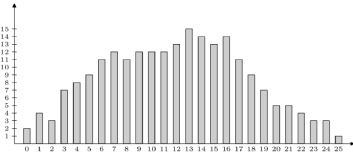
3. W konkursie matematycznym startowało 220 uczniów. Każdy zawodnik mógł uzyskać maksymalnie 25 punktów. Poniższy diagram słupkowy pokazuje, ilu uczniów uzyskało poszczególne liczby punktów od 0 do 25. Do następnego etapu konkursu przechodzi 20% uczestników, którzy uzyskali najlepsze wyniki. Wojtek dostał 19 punktów. Czy przejdzie on do następnego etapu? (Odp.: tak).
   
4. Wybierz stronę dowolnego tekstu napisanego w języku polskim. Policz wszystkie litery w tym tekście oraz policz liczbę wystąpień każdej litery alfabetu polskiego.
   Możesz to łatwo zrobić zapisując cały tekst na przykład w programie Word,a następnie zamieniając każdą literę na przykład na gwiazdkę (użyj: Zamień,a następnie Zamień wszystko; komputer wskaże Ci liczbę dokonanych zamian – jest to liczba wystąpień zamienianej litery w całym tekście). Oblicz częstość występowania każdej litery w całym tekście. Sporządź diagram słupkowy znalezionych częstości występowania. Porównaj otrzymany diagram z diagramami otrzymanymi przez Twoich kolegów na podstawie wybranych przez nich tekstów. Czy te diagramy są podobne? Zrób analogiczne ćwiczenie dla tekstów napisanych w innych językach (na przykład w języku angielskim). Czy otrzymane diagramy częstości są podobne do diagramów dla języka polskiego?
   Odp.: odpowiednie diagramy słupkowe sporządzone na podstawie pierwszych 72 wersów Pana Tadeusza oraz pierwszych czterech akapitów powieści Hobbit
   w języku angielskim wyglądają następująco: 
   
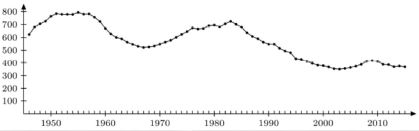
5. Znajdź dane dotyczące liczby urodzin dzieci w Polsce w latach 1946–2015. Sporządź wykres liniowy tych danych (odpowiednio zaokrąglonych). Czy możesz wyjaśnić skąd się biorą znaczne różnice w liczbie urodzin (tzw. wyże i niże demograficzne)? Odp.: ten wykres wygląda następująco (dane w tysiącach urodzin) 
6. Maciek dostał 10 ocen z matematyki. Oto 9 z nich: 2, 2, 2, 3, 3, 4, 5, 5, 6. Średnia arytmetyczna wszystkich dziesięciu jego ocen jest równa 3,6. Wyznacz brakującą ocenę. 
7. Oblicz pole kwadratu według wzoru P = a² dla następujących wartości a: a=¹/₄, a=¹/₂, a=³/₄, a=1, a=⁵/₄, a=³/₂, a=⁷/₂ oraz a=2. Każdą z obliczonych wartości zaznacz na wykresie w układzie współrzędnych, w którym jednostka na osi poziomej (na której są zaznaczone wyłącznie wartości a) ma długość 6 cm, a jednostka na osi pionowej (na której są zaznaczone obliczone wartości P) ma długość 2 cm. 
8. Janek poszedł na wycieczkę pieszą. Od godziny 8:00 do godziny 10:00 szedł pod górę z prędkością 4 km/h; od godziny 10:00 do godziny 10:30 odpoczywał na szczycie góry; od godziny 10.30 do godziny 12:00 szedł z góry z prędkością 6 km/h; od godziny 12:00 do godziny 14:00 szedł po poziomej drodze z prędkością 5 km/h. Oblicz, jaką drogę przeszedł od początku wycieczki do danej chwili. Obliczone wielkości zaznacz na wykresie w układzie współrzędnych.